信息增益:特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即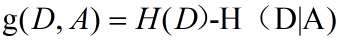
一般,H(Y)与条件熵H(Y|X)之差称为互信息。
熵是什么呢?
熵表示随机变量不确定性的度量。熵越大,该变量的不确定性越强。
熵的计算方法,设X为离散型随机变量,其概率分布为
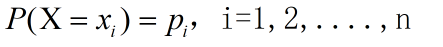
则其熵的计算方法为:
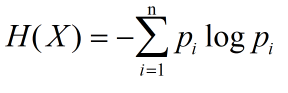
熵越大,变量的不确定性越大。且
0<=H (p)<=log n,可知当变量的取值数量越少时熵的范围越小,其实从另一个角度来思考,可取的值越少,不确定性就越简单,这也正对应了熵越大,变量的不确定性越大,熵越小,变量的不确定性越小。
上面解释熵用的是离散型的随机变量,如果是连续的随机变量呢?
方法还是一样的,如果是联系的随机变量,其可取得范围越大,熵越大,不确定性越大。
比如一对情侣约会,女孩跟男的说:“明天早上六点到七点你在某某地等我或者下午三点到五点你在某某地等我,你选个时间段吧!”
男的说:“我不想一直等你,我就在其中一个时间段去五次,碰到就约会,碰不到就拜拜”
显然这个男得比较“直”但同时,男的应该选早上六点到七点,这个时间碰到女朋友的可能性更大。
现在我们将熵得计算公式转化一下,得到下式:
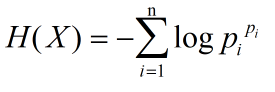
我们发现最大熵得大小与下面这个函数关系比较大:
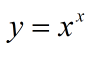
这里 0<x<=1,将p看作x,可知h(x)与y成反比关系,y越大,h(x)越小。
这里给出y在x从0-1的函数图像
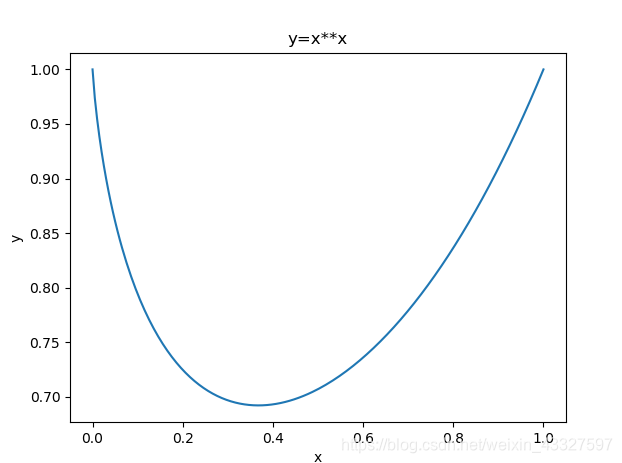
其实对于最大熵还有一个不等式:
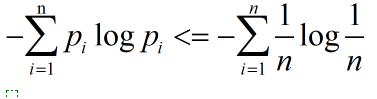
这个不等式的意思是当一个随机变量的取值有n个时,且对每个取值都有一个概率时,此时的熵一定小于等于每个取值概率相等时的熵,其实这就是我们在前面提到的0<=H(p)<=log n。
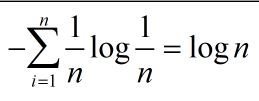
这里我们其实也可以举个例子,比如现在一个不透明盒子,盒子上面有一个只可以伸进手的洞,现在盒子里有五种颜色的球,红黄蓝绿紫,且数量都为五十个,现在问,随机从里面拿一个球,请问,为什么颜色。
你应该会觉得都一样啊,不好猜。
现在改一改,将八个蓝的变成红的,跟刚才一样随机取一个,你现在肯定觉得红的可能性更大了,蓝的几乎可能性很小了,其他三种差不多吧!其实这时候熵变小了,不确定性变小了。
上面讲了很久的熵,现在我们在提提条件熵
看到这里,有些人可能会想到概率论里的条件概率,条件熵与条件概率有些相似,H(X|Y)即表示随机变量Y在已知随机变量X已发生的条件下的不确定性。
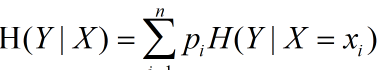
pi=P(X=xi),i=1,2,3…,n.
还得提到一个点,在信息论中,熵越大也代表某个事件的信息量越大。
谈完了熵和条件熵,现在我们再来看上面那个式子,g(D,A)=H(D)-H(D|A),现在将D看作数据集,A看作特征,信息增益g(D,A)是否就是数据集原本的不确定性,或者说它不考虑特征时的信息量减去考虑某个特征时的信息量。
这样得到的结果就是考虑那个特征时减少的信息量,信息量减少的越多,信息增益越大,也就是说这个特征对数据集的划分影响越大。
所以信息增益可以作为决策树选择特征区划分数据集的方法。