持续更新!
基本上只是整理了一下框架qwq。
。。怎么说呢,最基础的模板我就我不说了吧qwq,具体可以参考一下这位大佬写的博客:最大流,最小割,费用流
费用流
跑最大费用流的时候可以把边权都变成负的,然后按照原先的方法跑最小费用流即可。
每个点只能经过一次的时候,就拆点,然后两个点之间连容量为1费用为0的边。连路径的时候,强制从v'向u连边。
经典费用流模型
- 连续M个元素最多选K个
给你N个元素,每个元素都有一个权值ai(可正可负),要求从中你选出一些,满足对于任意相邻的M个元素当中最多只有K个元素被选出,使得总权值最大。
BZOJ1283 序列
二分图
设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
判定二分图:黑白染色,如果有矛盾,就不是二分图。
如果进行到最后都没有矛盾,那就是二分图。
或者说,如果一个图里面没有奇环,就是二分图。
树是一个二分图。
二分图最大匹配

就是一个二分图中最多能够匹配的对数。
建立一个源点S,一个汇点T,S点向左点集X连边,右点集Y向T点连边,两个点集间从左向右连边,容量都是1,求最大流即可。
很显然一个流就代表一个匹配
(求最大流的算法主要是KM((N*M^2)),dinic算法((M*N^2))。dinic算法求二分图最大匹配的时间复杂度是(M*sqrt N))
KM算法求最小带权完美匹配的模板:
inline int match(int x)
{
S[x]=true;
for(int j=1;j<=n;j++)
if(lx[x]+ly[j]==w[x][j]&&!T[j])
{
T[j]=true;
if(!to[j]||match(to[j]))
{
to[j]=x;
return true;
}
}
return false;
}
//以上是寻找最大匹配的匈牙利算法
inline void update()
{
int d=INF;
for(int i=1;i<=n;i++)
if(S[i])
for(int j=1;j<=n;j++)
if(!T[j])
d=min(d,lx[i]+ly[j]-w[i][j]);
for(int i=1;i<=n;i++)
{
if(S[i]) lx[i]-=d;
if(T[i]) ly[i]+=d;
}
//修改左右顶标的值
}
inline void KM()
{
for(int i=1;i<=n;i++)
{
lx[i]=ly[i]=to[i]=0;
for(int j=1;j<=n;j++) lx[i]=max(lx[i],w[i][j]);
}
//初始化,左边的顶标都等于该点连接的边中最大的边的权值
for(int i=1;i<=n;i++)
{
while(233)
{
for(int j=1;j<=n;j++) S[j]=T[j]=0;
if(match(i)) break;//若找到了当前点的增广路,就可以跳出寻找下一个点的了
else update();//若未找到增广路,则修改顶标的值,这样子下次就可以找到增广路了
}
}
}
KM算法的顶标:
可行顶标十一个节点函数l,使得对于任意弧((x,y)),有(l(x)+l(y)ge w(x,y))。相等子图是G的生成子图,包含所有点,但只包含满足(l(x)+l(y)=w(x,y))的所有边((x,y))。
定理:如果相等子图有完美匹配,则该匹配是原图的最大权匹配。
如何确认一条边/点是否一定在二分图最大匹配中
- (dinic+tarjan)在跑完dinic的残量网络上面SCC缩点,对于一条边,如果它满流,且左右端点不在一个SCC中,那么它一定在二分图最大匹配上。
yy的证明:如果在一个SCC中,一定能找到其他的替代边。 - (匈牙利算法,确认一个点)先ban掉当前点,再增广的时候强行不选,然后再对它的匹配点进行增广,如果有其他的匹配,那么它不一定在二分图最大匹配上,反之则一定。
二分图最大权匹配
别的和最大匹配一样,但是给X到Y的边加费用为对应的边权,然后求S到T的最大费用流(注意这里不是最大费用最大流,因为那个是要求在最大流基础上的最大费用,可能就不是全局最大费用了)
二分图最小点覆盖
就是选出来最少数量的点,使得这些点所连接的边的并集覆盖掉所有的边。
定理:最小点覆盖=最大匹配
证明:首先,对于flow个最大匹配,每个匹配都需要一个点,也就是最少需要flow个点。实际上最多也是只需要flow个点。一条边只需要一个点就可以了;选了flow个点后,还有一条边两端的点都不在这个点集中说明还可以增广,这就和最大流的假设违背了。
一般适用于:
- 两种选择,至少要选择一个,每个选择有代价的最优化问题(比如说BZOJ1741 asteroids )
二分图最小点权覆盖集
定理:最小点权覆盖=最小割=最大流
证明:S-X和Y-T的连对应点权容量的边, X-Y的连容量inf的边,然后求最小割,首先中间的边不会被割,也就是左右边的边选一些割掉(左右选一些点作为覆盖点)。
证明即是建图方式。
二分图最大独立集
在二分图中选出来一些点,使得这些点两两之间都没有边相连。
定理:最大独立集=点数-最小点覆盖
yy的证明:一条边只有两个点,如果排除这些最小点覆盖的集合,显然每条边只剩下剩下的那个点。这些点只有通过边才能与其他点相连,但是它们相连的边上的另外一点都已经被排除,所以相当于它们“与世隔绝”,所以这些点集就是最大独立集的数量。
二分图最大点权独立集
定理:总点权-最小割
yy的证明:正难则反,这个东西肯定是总点权减去一个什么值,然后这个值还要尽可能小,而且减去这个东西后还要保证留下来的点两两之间互不到达。将这个图断开的最小代价就是最小割了,所以自然减去的东西就是最小割(最小点权覆盖集)了qwqwq
小结:
二分图最大匹配=二分图最小点覆盖=最小割=最大流=n-最大独立集。
二分图最小权覆盖和二分图最大权独立集互补。
DAG最小路径覆盖(不相交)
什么是最小路径覆盖呢?就是选出若干个路径,使得这些路径的并经过所有的点。
把原图的每个点V拆成Vx和Vy两个点,如果有一条有向边A->B,那么就加边Ax−>By。这样就得到了一个二分图。那么(定理)最小路径覆盖=原图的结点数-新图的最大匹配数。
yy的证明:把原先的每一个点都看成一条路径,每连一条边就是等于将两个点合并起来,路径数量-1。
例题:BZOJ2150部落战争 题解
DAG最小路径覆盖(可相交)
和上面的大概相同,先用floyd求出原图的传递闭包,即如果a到b有路径,那么就加边a->b。然后就转化成了最小不相交路径覆盖问题。
例题:POJ2594 题解
霍尔定理(hall定理)
二分图G中的两部分顶点组合成的集合分别为X,Y。G中有一组无公共点的边,一端恰好为组成X的点(完美匹配)的充分必要条件是:X中的任意K个点至少与Y中的K个点相邻。
对于X中的一个点集W,令(N_G(W))为W的所有邻居,霍尔定理即对于任意W,(|W|<=|N_G(W)|)
证明:(来自wzd dalao的博客)
- 必要性证明
假如一个二分图G存在完美匹配,且不满足Hall定理。 那么对于某k个点,它们连向的都不足k个点。 那么它们是怎么都被匹配上的??? 很显然必要性正确。 - 充分性证明
假如一个二分图G不存在完美匹配,且满足Hall定理。 那么假如有一种最大匹配的方案,既然不存在完美匹配,可以找到至少一个未被匹配的点。 因为这个二分图满足Hall定理,所以这个点一定连向了至少一个点。 假如这个点不在最大匹配中,它们就匹配了,怎么可能呢??? 那么这个点在最大匹配中!所以一定有一个点和它匹配了。 因为这个二分图满足Hall定理,所以这个点又一定连向了除它匹配的点外的至少一个点。 假如这个点不在最大匹配中,一条增广路找到了,怎么可能呢??? 那么这个点在最大匹配中!所以…… 看懂了吧!我们一定能推出矛盾! 所以充分性正确。
霍尔定理(hall定理)拓展
对于X,Y二分图最大匹配数=(|S|-max{|W|-|N(W)|}),其中S是X全集的个数,W是S的子集。
这个结论可以让我们不通过建图,就可以知道最大匹配数量。
最小割
最小割,图中所有的割中,边权值和最小的割为最小割。
最小割是解决利益冲突情况下的利益最大化问题
可能割边
就是有可能在最小割中的边。
定理:当且仅当该边满流且残余网络(包括反向边)中该边两端点处于不同SCC时,该边可能在最小割中。
关键割边
一定在最小割中的边。
将可能割边的容量加一,如果求得的最小割增大,证明该边一定是关键割边。
1.跑一遍网络流之后,对残量网络做SCC,满流且边的两个端点不在同一个SCC中的边是可能割边。
2.跑一遍网络流之后,对残量网络做SCC,满流,边的两个端点分别和S和T在同一个SCC里,这个边是关键割边。
-
证明1:考虑如果减少一条边的容量之后,最小割变小了,证明这条边可能存在于最小割之中。那么反过来,如果(u,v)在同一个SCC中,我们把u→v这条边的容量减小d,那么我们把这个环上的所有边的容量都减少d,仍然满足流量平衡,意味着最大流即最小割不变。反之最大流即最小割改变,那么这条边可能存在于最小割中。
-
证明2:增加一条边的容量,如果最小割增加,意味着这条边必定在最小割中。因为u→是满流的边,所以沿反边u可达S,T可达v 。如果S,u在同一个SCC,T,v在同一个SCC中,说明S到u上还有增广路,v到T上还有增广路,那么u→v的流量增加最小割也会增加,此时u→v必定在最小割中。
输出任意最小割方案
(如果只输出左右端点,不考虑中间连边——即INF时)跑一遍dinic,然后在残量网络上记录done数组,最后一遍bfs左边没有访问到的点和右边访问到的点就是最小割。
无向图最小割树。(分治最小割)
一些性质:
对于两个点(s,t)的最小割。这个最小割将将所有点分成左右两个集合X、Y。对于X中任意一点a与Y中任意一点b, (a,b)的最小割小于等于(s,t)的最小割。因此,每次递归计算分成的两个集合的最小割,更新答案。
也就是说明,每求一次最小割,都可以把一个大点集分成两个小点集,显然最后能分的次数是n-1次,也就是无向图不同的最小割最多n-1个。
例题:BZOJ2229/ZJOI2011 最小割 题解
最大权闭合子图
什么是闭合子图:给定一个有向图,从中选择一些点组成一个点集V。对于V中任意一个点,其后续节点都仍然在V中。
入门的话建议大家先去看这篇博客戳我
定理:最大权闭合子图=总点权-最小割
最大权闭合子图建模方式:先把答案加上所有的正权值,然后从源点向所有的正权点连一条流量为权值的边,所有的负权值的点向汇点连一条流量为权值相反数的边。原图中的所有的限制关系(i,j)均建立一条从i到j的流量为inf的边,最终的答案减去这个图的最小割就可以了。
最大密度子图
和分数规划有关,蒟蒻还不会。。。。回来再补。
平面图与对偶图
参考来自这位dalao的博客,在此表示感谢!
什么是平面图?任意两边之间的交点只能是顶点。
什么是对偶图?设有平面图G=(V,E),满足下列条件的图G'= (V',E') 称为图G的对偶图:G的任一面Ri内有且仅有一点Vi';对G的域Ri和Rj的共同边界Ek,画一条边Ek'=(Vi',Vj')且只与Ek交于一点;若Ek完全处于Ri中,则Vi'有一自环Ek'。
之间的关系:平面图最小割=对偶图最短路
作用:用求最短路来代替最小割,降低时间复杂度。
图片示例:
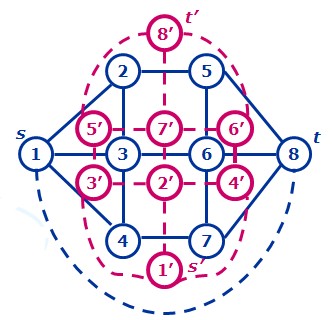
(蓝色的是平面图,紫色的是对偶图)
例题:NOI2010海拔 题解戳我
混合图欧拉回路
发现已经有大佬写啦!那就贴上好了qwq 戳我
给出一个有向图, 问至少删掉多少条边使得这个图有欧拉回路
设pi=in[i]-out[i]。如果pi>0,从S连向i,否则i连向T,容量为|pi|.然后一条有向边(u,v),网络流中连(v,u,1,1)◦求最小费用最大流,一条流表示把中间的边都删掉了,满流就代表着把入度出度不平衡的点给平衡了。
有上下界的网络流
