1、问题与分析
问题:
- 如何使用较少的乘法次数求 (x^{27})?
- 方法:缓存中间结果,避免重复计算
过程演示:
[x^3 = x * x * x, x^9 = x^3 * x^3 * x^3, x^{27} = x^9 * x^9 * x^9
]
[x^2 = x * x, x^4 = x^2 * x^ 2, x^8 = x^4 * x^4, x^{16} = x^8 * x^8, x^{27} = x^{16} * x^8 * x^2 * x
]
上面的方法利用的其实就是分治思想:
- 问题的规模是n,把n分解
- 如果n是偶数,(n = 2 * displaystylefrac{n}{2});否则 (n = 2 * displaystylefrac{n}{2} + 1)
- 因此,(x^0 = 1)
[x^n = egin{cases} (displaystyle{x^2})^{frac{n}{2}} quad n is not even \ (displaystyle{x^2})^{frac{n}{2}} * x quad otherwise end{cases}
]
- 最坏情况下,n始终为奇数
2、代码求解
2.1、递归代码
2.2.1、代码
int power(int x, int n)
{
if (0 == n)
return 1;
if (0 == n % 2)
return power(x * x, n / 2);
return power(x * x, n / 2) * x;
}
2.1.2、复杂度分析
- 时间复杂度:(O(logn)),即为递归的层数
- 空间复杂度:(O(logn)),即为递归的层数。这是由于递归的函数调用会使用栈空间
2.2、改写递归为迭代
2.2.1、代码
int power(int x, int n)
{
int res = 1;
if (0 == n)
return 1;
for (; n > 0; n = n >> 1)
{
if (1 == n % 2)
res *= x;
x *= x;
}
return res;
}
2.2.2、分析与理解
这个算法该如何理解,我们可以借助LeetCode的官方题解(https://leetcode-cn.com/problems/powx-n/solution/powx-n-by-leetcode-solution/)来分析:

我想了很长时间,令我困惑的点是在每一次迭代时,n为奇数和n为偶数的情况为什么会是这样处理,现在借助这个题解,我们理解起来会容易很多。
我们把一开始的x给剥离出来,它到最后一次迭代时,它的幂一定是不超过n的最大的2的整数次幂,比如,n为77时,那么x最后的幂就是64,n为60时,x最后的幂就是32;我们可以列一个式子:
[① x
ightarrow x^2
ightarrow x^4
ightarrow^{+} x^9
ightarrow^{+} x^{19}
ightarrow x^{38}
ightarrow^{+} x^{77}
]
[② x
ightarrow x^2
ightarrow x^4
ightarrow x^8
ightarrow x^{16}
ightarrow x^{32}
ightarrow x^{64}
]
我们迭代的顺序是从后往前,所以x的值的变化是这样的:
[③ x^{64}
ightarrow x^{32}
ightarrow x^{16}
ightarrow x^8
ightarrow x^{4}
ightarrow x^{2}
ightarrow x
]
这里解释一下 (x^{9} ightarrow^{+} x^{19}) 中额外乘的 x 在之后被平方了两次,因此在 (x^{77}) 中贡献了 (x^{2^2} = x^4),我们知道,我们的 x 只保存了 x 的2的乘幂次方(即②式中的各个数),而遇到奇数时,多出来的一个 x 所贡献的次数就保存在了res中,我想,大家所疑惑的就是为什么就要恰好保存迭代到那一次时的 x,我们用式子来解释一下:
我们把 (x^9) 中多出来的一个 x 给拆解出来,那么:
[x^{8 + 1}
ightarrow x^{16 + 2}
ightarrow x^{32 + 4}
ightarrow x^{64 + 8}
]
即,在 (x^{77}) 中贡献了 (x^{2^3} = 8) 。类似地,我们把奇数次的迭代时的需要贡献的值保存在 res 中,最后再与最后的 x 的值合并,就得到最后的结果了。
2.2.3、复杂度分析
- 循环次数为 (logn) 次
- 最好情况下的乘法次数为 (logn) 次:n%2 始终为0
- 最坏情况下的乘法次数为 (2logn) 次:n%2始终为1
- 算法时间复杂度为 (O(logn))
- 算法空间复杂度为 (O(1))
3、其他分解方式(扩展)
3.1、分解方式
- 问题的规模是n,仍然按照n分解
- 如果n是偶数,(n = displaystylefrac{n}{2} + displaystylefrac{n}{2});否则,(n = displaystylefrac{n}{2} + displaystylefrac{n}{2} + 1)
- 因此,(x^0 = 1)
[x^n = egin{cases} displaystyle{x^{frac{n}{2}}} * displaystyle{x^{frac{n}{2}}} quad n is not even \ displaystyle{x^{frac{n}{2}}} * displaystyle{x^{frac{n}{2}}} * x quad otherwise end{cases}
]
- 最坏情况,还是n始终为奇数的情况
3.2、递归代码
3.2.1、代码
int power(int x, int n)
{
if (0 == n)
return 1;
if (0 == n % 2)
return power(x, n / 2) * power(x, n / 2);
return power(x, n / 2) * power(x, n / 2) * n;
}
3.2.2、复杂度分析
- 显然,复杂度为 (O(n)),这是很坏的算法
3.2.3、解决办法
代码
int power(int x, int n)
{
int tmp;
if (0 == n)
return 1;
tmp = power(x, n / 2);
if (0 == n % 2)
return tmp * tmp;
return tmp * tmp * x;
}
- 显然,易知:(T(N) = T(frac{N}{2}) + O(1))
- 故时间复杂度为:(O(N))
下面是在stackexange网站找到的复杂度证明:
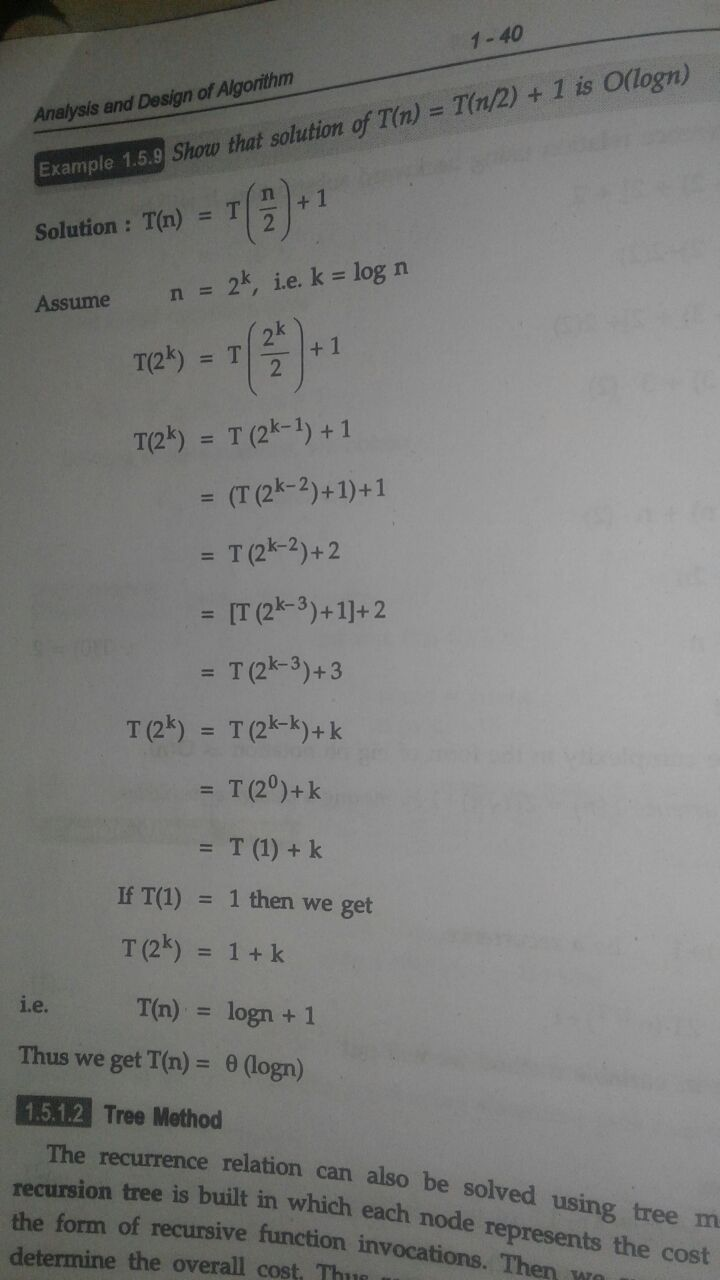
4、以3为底(扩展)
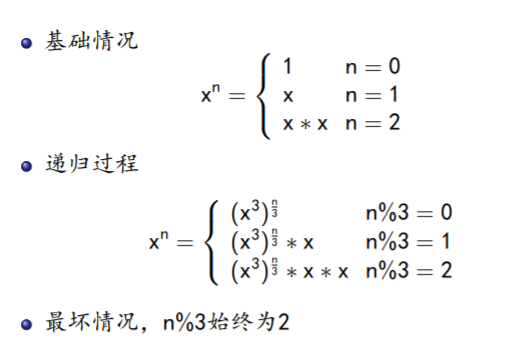
递归代码
int power(int x, int n)
{
if (n == 0)
return 1;
if (n == 1)
return x;
if (n == 2)
return x * x;
if (n % 3 == 0)
return power(x * x * x, n / 3);
if (n % 3 == 1)
return power(x * x * x, n / 3) * x;
return power(x * x * x, n / 3) * x * x;
}
时间复杂度分析:
- (T(N) = logN)
迭代代码
int power(int x, int n)
{
int res = 1;
if (n == 0)
return 1;
for (; n > 0; n /=3, x = x*x*x)
{
if (n % 3 == 1) res *= x;
if (n % 3 == 2) res *= x*x;
}
return res;
}
时间复杂度分析:
- (T(N) = T(N / 3) + 4, T(0) = 0)