遇见的第一道决策单调性优化DP,虽然看了题解,但是新技能√,很开森。
先%FlashHu大佬,反正我是看了他的题解和精美的配图才明白的,%%%巨佬。
废话不多说,看题:
题目大意
已知一个长度为n的序列a1,a2,...,an。
对于每个1<=i<=n,找到最小的非负整数p满足 对于任意的j, aj < = ai + p - sqrt(abs(i-j))
数据范围
洛咕上也没给,我能怎么办啊
非正解做法一:暴力
应该都会吧,(O(n^2))枚举。洛谷上貌似40pts。
非正解做法二:ST表优化
首先,我们将原式整理,可得(pgeqslant a_j-a_i+sqrt{left | i-j
ight |}),最终(p_i)即是(max{left lceil a_j-a_i+sqrt{left | i-j
ight |}
ight
ceil })。
然后,我们发现,其实需要向上取整的只有(sqrt{left | i-j
ight |})这一部分,而它向上取整的值是连续分布的,即0,1,2,2,2,3,3,3,3,3,4......且如果知道i和j的值时,我们很容易知道同一个数开始的位置和结束的位置。
然后我们就可以用ST表来维护区间最大值,预计得分50pts。
(我没想到的)正解
经过观察式子,我们知道(p_i)的值取决于(a_j+sqrt{left | i-j
ight |}),现在,我们记这个值为(f_j),且(f_j)是关于i的一个函数,(igeqslant j)。那么,所有的(f_j)大概会长成这个样子:
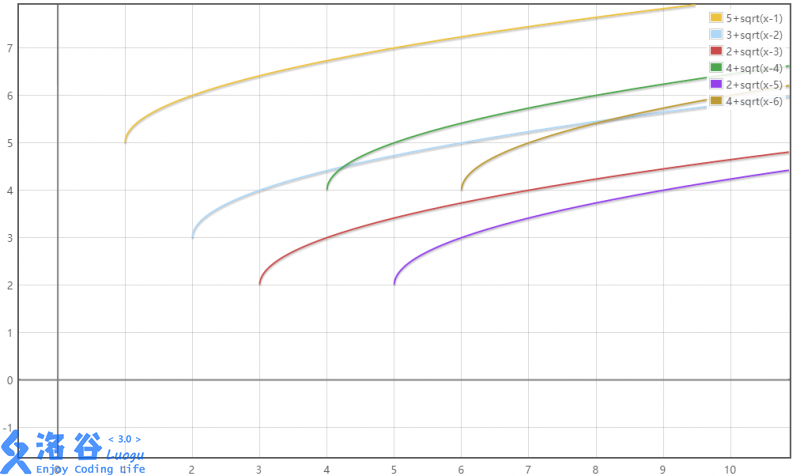
不难看出,每个(f_j)都是单调递增的,形状都是一样的(但定义域和值域不同),且斜率越来越小(这貌似叫上凸?)。
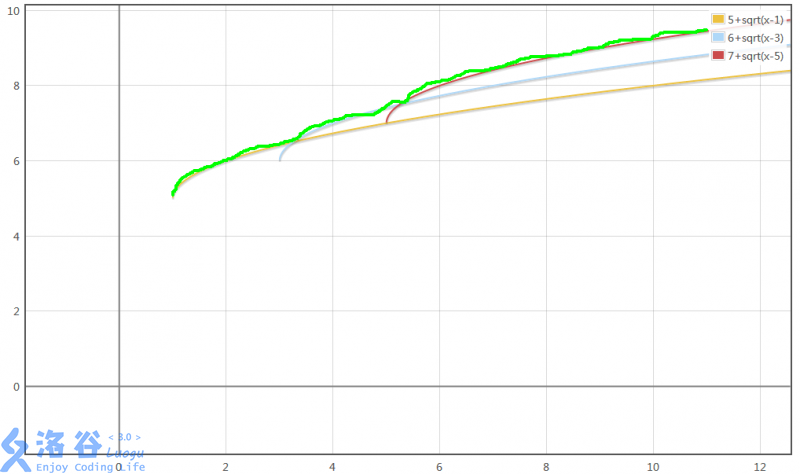
但是如果函数长成这张图那样,我们真正需要的只有上面的那一条绿线。
假设在程序中我们有了这张图,问题就变得hin简单,用最高的那个函数一算就可以辣(比如这张图就是上面那个黄色的)。
于是,问题转化为如何找出最高的那个(f_j)了。(f_j)还有一个很好的性质,就是对于最高的那个(f_j),它的巅峰时期绝对是一段连续的区间(因为上凸嘛),且最高的那条一定是在某两条函数图像的交点处改变的。
然后,我们发现这个东西用单调队列很好维护,我们可以顺带求出i位置的答案。此处令(cur)为当前枚举到的(j),(q)为单调队列(存的是(j)),(h)为队头指针,(t)为队尾指针,(isx[i])为队列中第(i)个(f_j)与队列中第(i+1)个(f_j)的交点横坐标,(intersectionX(i,j))返回的是(f_i)与(f_j)交点的横坐标。我们先按(j)从小到大把(j)加入,但我们要怎样维持队列的单调性呢?
1.当(isx[t-1] geqslant intersectionX(q[t],cur))时,那么就可以把(q[t])弹出(想一想,画一下图就很清楚了)
2.把(j)插入到队尾
3.当(isx[h] leqslant cur)时,那么就可以把(q[h])弹出(显然嘛)
操作完后,(q[h])就是我们要的最高的(f_j)的(j)了,然后我们就可以更新(i)位置的答案啦。
那么(intersectionX(i,j))该怎样求呢?因为问题是定义在正整数域上的,我们就二分一下。
最后,注意一下砸,因为我们要从小到大加入j,而枚举点可能会在中间,所以我们要正着跑一遍,再倒着跑一遍,两遍取一下(max)。
上代码:
#include <bits/stdc++.h>
using namespace std;
#define re register
#define N 20000000
int n, isx[N+5], q[N+5], a[N+5];
double f[N+5]; //答案数组
double calc(int x, int y) { //计算a[y]+sqrt(x-y)
return a[y]+sqrt(double(x)-y);
}
int intersection(int f1, int f2) {
int l = 1, r = n, mid, ret = r+1; //ret要设成n+1,因为在1~n中可能没有交点
while(l <= r) { //二分交点
mid = (l+r)/2;
if(calc(mid, f1) <= calc(mid, f2)) ret = mid, r = mid-1;
else l = mid+1;
}
return ret;
}
void solve() {
for(re int h = 1, t = 0, i = 1; i <= n; ++i) {
while(h < t && isx[t-1] >= intersection(q[t], i)) --t; //队尾删除操作
isx[t] = intersection(q[t], i), q[++t] = i; //插入到队尾
while(h < t && isx[h] <= i) ++h; //队头弹出操作
f[i] = max(f[i], calc(i, q[h])); //更新答案
}
}
int main() {
ios_base::sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n;
for(re int i = 1; i <= n; ++i) cin >> a[i];
solve();
for(re int i = 1, j = n; i < j; ++i, --j) swap(a[i], a[j]), swap(f[i], f[j]); //反转序列
solve();
for(re int i = n; i >= 1; --i) cout << ceil(f[i])-a[i] << endl; //计算答案
return 0;
}