问题定义:
输入:空间上n个点的集合Q
输出:最近点的距离
定义
Dis(X,Y)为点X和点Y之间的距离
Cross(Q1,Q2)为横跨Q1和Q2两个点集的最小距离
【一维】
思路:
1. 划分:将数轴上的点用中位数m分成两个集合
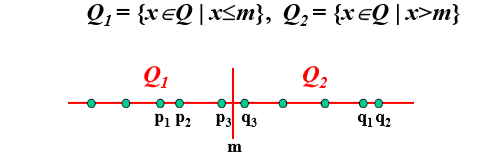
2. 求解:递归在Q1和Q2中求解子问题
3. 合并:MIN(Q)= min(MIN(Q1),MIN(Q2),Cross(Q1,Q2))
时间复杂度分析:
划分:O(n);求解:2T(n/2);合并:O(1);
T(n)= 2T(n/2)+O(n)=O(nlogn)
伪代码:
//参数A:点的数组(已经按坐标排列)
//参数low:最左边的点下标
//参数high:最右边点下标
Find_MinDis(A,low,high)
if(high-low == 1) return Dis(A[low],A[high]);
else if(high - low > 1)
mid = (low+high)/2
Left_min = Find_MinDis(A,low,mid)
Right_min=Find_MinDis(A,mid+1,high)
Cross_min=Dis(A[mid],A[mid+1])
return Min(Left_min,Right_min,Cross_min);
【二维】
思路:
划分: 将点按照横坐标的中位数划分成两部分
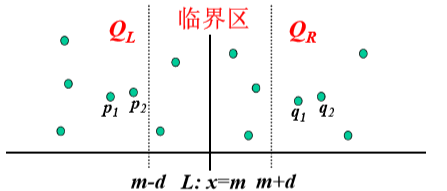
记S1和S2中的最小距离d1和d2,设d=min(d1,d2)。
求解:分别递归的计算出S1和S2的最小距离
合并:MIN(S)= min(MIN(S1),MIN(S2),Cross(S1,S2))
问题在于:如何找到横跨S1和S2的两点最小距离
若使用暴力搜索 ,理论上需要进行n^2/4次计算
下面使用方法来缩小寻找点的范围:
1. 容易得知:对S1的任意一个点p来说,满足条件的点一定落在S2中d*2d的范围内
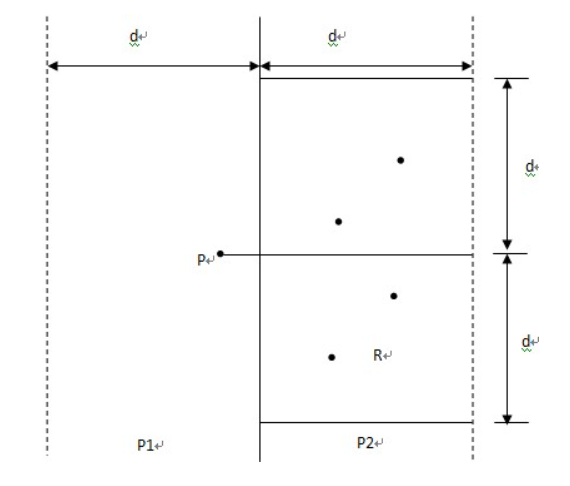
2. 进一步缩小范围,S2中任意两点距离大于等于d,由抽屉原理得知,任意两点不在同一个小矩形中
 即只需考虑最多6个点
即只需考虑最多6个点
3. 这样就将时间缩减到6*n/2=3n,即O(n),总的时间复杂度依然是O(nlogn)