第三章:集合与关系
3.4 序偶与笛卡尔乘积
1 有序组(序偶、三元组、n元组)
2 笛卡尔乘积
一、有序组
1.序偶:由两个元素,按照一定次序构成的二元组称为
一个序偶,记作<x,y>。
注: <x,y>=<u,v>的充要条件为x=u,y=v
2. 三元组:三元组是一个序偶<<x,y>,z>,记作<x,y,z>。
注:<<x,y>,z>≠<x,<y,z>>
3. n元组: <<x1,…,xn-1>, xn>,记作<x1,…, xn-1, xn>。
例如:<a,b,c,d,e,f>
二、笛卡尔积



3.5 关系及其表示
1 关系的定义
2 关系的域
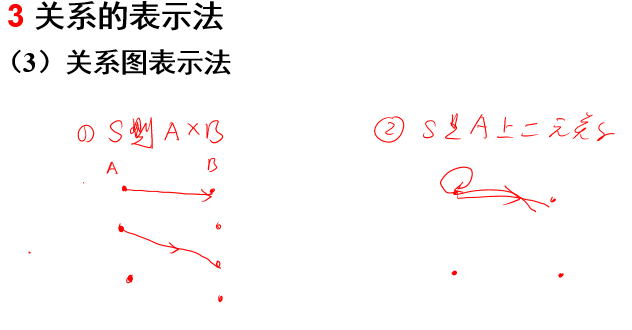
3 关系的表示法
- 集合表示法
- 矩阵表示法
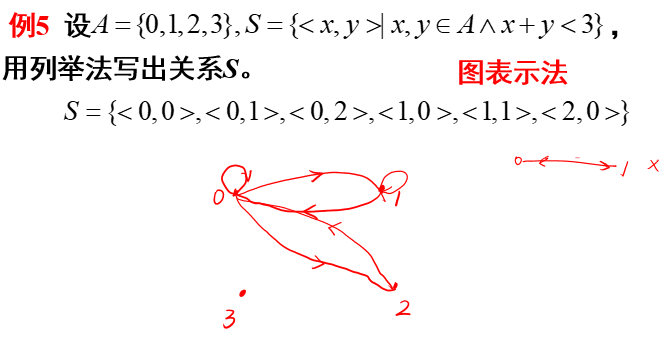
- 图表示法


(注意:a可以整除b 和 b除以a余数是0 是不等价的,两者唯一区别在于 可以说 0 整除 0 ,因为这符合整除的定义——存在c属于整数使b = a×c,但不能说0除以0余数是0,因为0不能做除数)

(即:把集合中所有序偶的前一个元素都拿出来构成的集合就是前域,把集合中所有序偶的后一个元素都拿出来构成的集合就是值域)



X到Y上的二元关系,X中的元素作为行,Y中的元素作为列


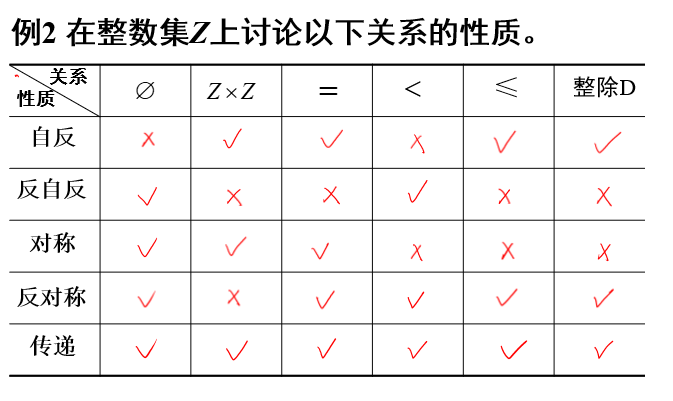
3.6 关系的性质
1 自反性
2 反自反性
3 对称性
4 反对称性
5 传递性
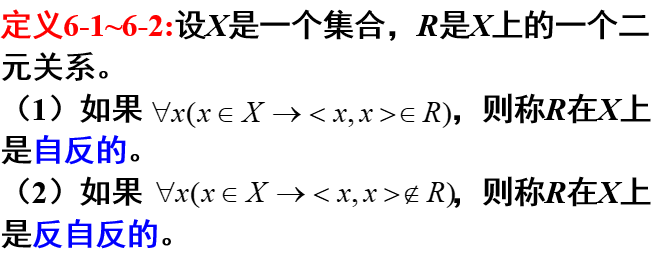


上图中:R1不自反是因为它缺少序偶<3,3>,自反性要求对于A所有前域和值域相等的序偶都必须出现。R1不反自反的原因是它出现了<1,1>、<2,2>,反自反性要求所有前域和值域相等的序偶都不能出现。
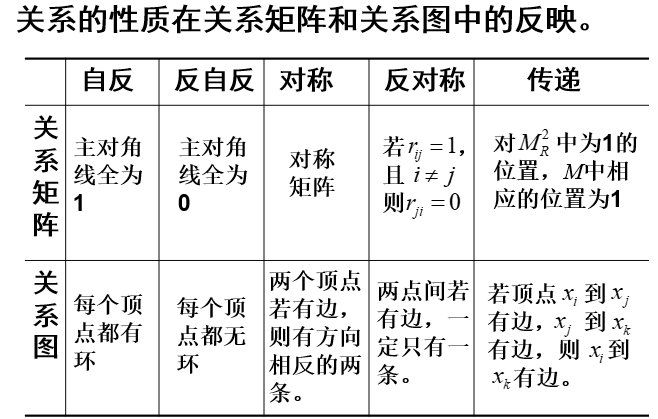
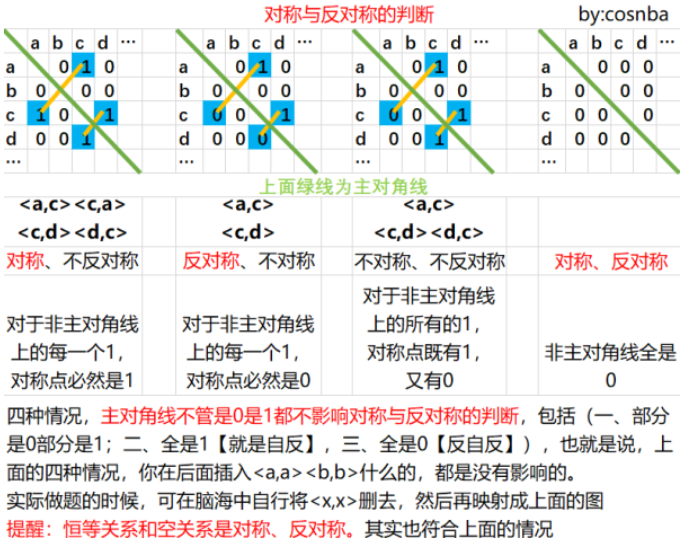
为了更好地理解对称和反对称,下转载这张图: