线图(状态压缩,dp,搜索,树的最小表示法)
观察样例。先模拟一下求线图的过程。
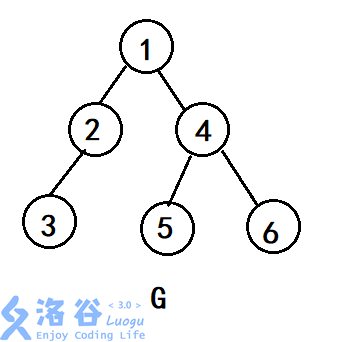
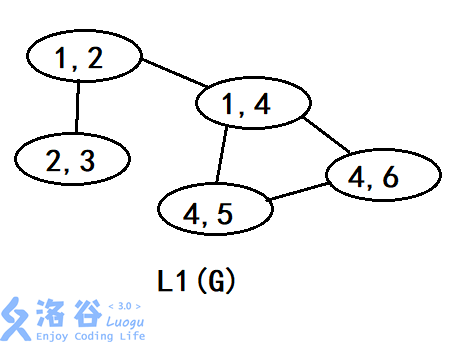


观察,发现原图上的每一个边数$<=k$的连通块都代表了线图上的几个点。且每一种连通块代表的点的个数一样,都为图的$k$阶线图的代表点的个数。
实际上,原图中是边数$=k$,但是实际上,一个图可能会生成类似三元环这样子的图(比如1-2,1-3,1-4连边后生成的图的线图),这种图在线图变换下与自己是一样的,所以是$<=k$
所以问题就转化成了:算出每种不同构的有根树,计算每个有根树的权重,计算每个有根树在原图内出现的次数。
算出每种有根树可以使用括号序列+最小表示法。可以先枚举一下树的括号序列,再用最小表示法去重。
树的最小表示法就是字典序最小的括号序列('('比')'小)。生成这个序列的方式是:dfs当前节点x的所有子树,得到子树的最小表示序列。把这个序列按照字典序排序,从小到大拼起来,在左边+'(',在右边加')'就得到了以x节点为根的树的最小表示法。判定两棵树是否同构,只要判定它的最小表示法序列是否相同即可。
实际上,在使用树的最小表示法+括号序列得到所有树后,发现树的个数只有1205种,可以对于每一种树计算它对应的权值,乘上出现次数即可。
接下来是计算权重。初始的权重是这棵树的$k$阶线图的点数。但是这并不是真正的权重,内部包含了这棵树的导出子图的贡献,它们在进行线图变换时也会生成点,要减去。
实际上,这样子看上去很暴力,但是这样子的复杂度只是$2^k$,并不是这道题的瓶颈。
考虑计算线图的权值(即它展开9次以后在图中代表的点数)显然暴力展开是不行的。这样子会生成$O(k^k)$个点,铁定超时。
但是发现这道题的$k=1~4$可以被推出来,可以把$L_k(G)$视为$L_4(L_{k-4}(G))$,前5层暴力展开,后5层使用公式计算。
公式如下:
$L(G)$显然是G的边数。
$L(L(G))$是树上的大小为2的折链,一个点可以产生$c(deg,2)$贡献,所以答案就是$sum c(deg,2)$
$L(L(L(G)))$是树上的一个类似$1-2 1-3 1-4$三条边构成的图,或者是一个三条边构成的链。
前者的贡献是$c(deg,3)$,后者的贡献是图上的2个点再伸出一条链的选择方案,就是$(deg[x]-1)(deg[y]-1)$(x,y为原图上的一条边,要-1是不能把x的伸出的链伸到y)
$L(L(L(L(G))))$可以被视为$L_3(L(G))$,(先鸽子)
计算出现的次数可以使用dp。设$f[i][j]$表示当前点i匹配情况为j的答案。设一个辅助数组g表示计算前面几个树的答案。
转移时,先把f[i]复制到g,用f[son][k]更新g[j],再把g复制给f[i]
还有一个问题:现在我们强行把树有标号化了。如果子树重复要除掉重复数的阶乘。
(下一步优化先坑一下)
历史
迷宫
树
胖
保镖
先说怎么求三维凸包。
三维凸包可以使用增量法求解,每次新增一个点,由原来的凸包变成现在的凸包。
可以从当前新增的点投射一条线穿过每个点,到一个平面上,删除里面的点,构成新的凸包。
这样子每次最多删除n个点,是O(n^2)的,且可以扩展到任意维的情况。
有更快的,但是这道题使用这个算法是足够的。