例9 生理周期
问题描述
人生来就有三个生理周期,分别为体力、感情和智力周期,它们的周期长度为 23 天、28 天和33 天。每一个周期中有一天是高峰。在高峰这天,人会在相应的方面表现出色。例如,智力周期的高峰,人会思维敏捷,精力容易高度集中。因为三个周期的周长不同,所以通常三个周期的高峰不会落在同一天。对于每个人,我们想知道何时三个高峰落在同一天。
对于每个周期,我们会给出从当前年份的第一天开始,到出现高峰的天数(不一定是第一次高峰出现的时间)。你的任务是给定一个从当年第一天开始数的天数,输出从给定时间开始(不包括给定时间)下一次三个高峰落在同一天的时间(距给定时间的天数)。例如:给定时间为10,下次出现三个高峰同天的时间是12,则输出2(注意这里不是3)。
输入数据
输入四个整数:p, e, i 和d。 p, e, i 分别表示体力、情感和智力高峰出现的时间(时间从当年的第一天开始计算)。d 是给定的时间,可能小于p, e, 或 i。 所有给定时间是非负的并且小于365, 所求的时间小于等于21252。
输出要求
从给定时间起,下一次三个高峰同天的时间(距离给定时间的天数)。
输入样例
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
-1 -1 -1 -1
输出样例
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
(1)编程思路1。
假设从当年的第一天开始数,第k 天时三个高峰同时出现。符合问题要求的k必须大于d、小于等于21252(23×28×33),并满足下列三个条件:
1)(k-p) % 23 == 0
2)(k-e) % 28 == 0
3)(k-i) % 33 == 0
对区间[d+1,21252]中的每个k都进行三个条件的判断,若同时满足三个条件,则k就是所求。
(2)源程序1。
#include <stdio.h>
int main()
{
int p,e,i,d,caseNo = 0,k;
while(scanf("%d%d%d%d",&p,&e,&i,&d) &&p!=-1)
{
++caseNo;
for(k = d+1;(k-p)%23!=0 || (k-e)%28!=0|| (k-i)%33!=0; k++);
printf("Case %d: the next triple peak occurs in %d days. ",caseNo,k-d);
}
return 0;
}
(3)编程思路2。
思路1中对区间[d+1,21252]中的每个k都进行三个条件的判断,开销很大,可以进行优化。
具体优化办法是:先从区间[d+1,21252]中找到第一个满足条件1)的体力高峰出现的时间k1,然后从k1、k1+23、k1+2*23、k1+3*23…这些时间中寻找第一个满足条件2)的情感高峰出现的时间k2,当然它也一定是体力高峰出现的时间;最后在k2、k2+23*28、k1+2*23*28、k1+3*23*28…这些时间中寻找第一个满足条件3)的时间k3。则k3-d就是所求的答案。
(4)源程序2。
#include <stdio.h>
int main()
{
int p,e,i,d,caseNo = 0,k;
while(scanf("%d%d%d%d",&p,&e,&i,&d) &&p!=-1)
{
++caseNo;
for(k = d+1;(k-p)%23;k++); // 枚举体力高峰
while ((k-e)%28!=0) k+=23; // 枚举情感高峰
while ((k-i)%33!=0) k+=23*28; // 找到三高峰
printf("Case %d: the next triple peak occurs in %d days. ",caseNo,k-d);
}
return 0;
}
习题9
9-1 硬币方案
问题描述
有50枚硬币,可能包括4种类型:1元、5角、1角和5分。
已知50枚硬币的总价值为20元,求各种硬币的数量。
例如:2、34、6、8就是一种方案。而2、33、15、0是另一个可能的方案,显然方案不唯一。
编写程序求出类似这样的不同的方案一共有多少种?
输入数据
无
输出要求
所有可能的方案,输出格式见输出样例。
输入样例
无输入
输出样例
1: 0 , 38 , 8 , 4
2: 1 , 36 , 7 , 6
3: 2 , 33 , 15 , 0
……
(1)编程思路。
直接对四种类型的硬币的个数进行穷举。其中,1元最多20枚、5角最多40枚、1角最多50枚、5分最多50枚。
另外,如果以元为单位,则5角、1角、5分会化成浮点型数据,容易计算出错。可以将1元、5角、1角、5分变成100分、50分、10分和5分,从而全部采用整型数据处理。
(2)源程序。
#include <stdio.h>
int main()
{
int a,b,c,d,cnt=0;
for(a=0;a<=20;a++)
for(b=0;b<=40;b++)
for(c=0;c<=50;c++)
for(d=0;d<=50;d++)
{
if(a*100+b*50+c*10+d*5==2000 && a+b+c+d==50)
{
printf("%d: %d , %d , %d , %d ",++cnt,a,b,c,d);
}
}
return 0;
}
(3)穷举优化。
上面的程序采用穷举法求解,比较简单。但在穷举结构的设置、穷举参数的选取等方面存在着改进与优化的空间。
一般来说,在采用穷举法进行问题求解时,可从两个方面来优化考虑。
1)建立简洁的数学模型。
数学模型中变量的数量要尽量少,它们之间相互独立。这样问题解的搜索空间的维度就小。反应到程序代码中,循环嵌套的层次就少。例如,上面的程序中,采用变量a、b、c、d分别表示1元、5角、1角和5分硬币的枚数,对这4个变量穷举,循环层次为4层。实际上这4个变量彼此间有两个条件在约束,或者枚数等于50,或者总价值为20元。因此,可以只穷举3个变量,另外一个变量通过约束条件求出,从而将循环层次减少为3层。
2)减小搜索的空间。
利用已有的知识,缩小数学模型中各个变量的取值范围,避免不必要的计算。反应到程序代码中,循环体被执行的次数就减少。例如,在穷举时,先考虑1元的枚数a,最多为20枚(即0<=a<=20),再考虑5角的枚数b,若采用总价值不超过20元约束,则其枚数最多为(2000-a*100)/50枚(即0<=b<=(2000-a*100)/50),之后考虑1角的枚数c,其枚数最多为 (2000-a*100-b*50)/10(即0<=c<=(2000-a*100-b*50)/10)。这样穷举的循环次数会大大减少。
采用上述思路优化后的源程序如下。
#include <stdio.h>
int main()
{
int a,b,c,d,cnt=0;
for(a=0;a<=20;a++)
for(b=0;b<=(2000-a*100)/50;b++)
for(c=0;c<=(2000-a*100-b*50)/10;c++)
{
d=(2000-a*100-b*50-c*10)/5; // 剩下的用5分硬币填充
if(a+b+c+d==50)
{
printf("%d: %d , %d , %d , %d ",++cnt,a,b,c,d);
}
}
return 0;
}
也可以采用总枚数不超过50枚约束。先考虑1元的枚数a,最多为20枚(即0<=a<=20),再考虑5角的枚数b,则其枚数最多为(50-a)枚(即0<=b<=(50-a),之后考虑1角的枚数c,其枚数最多为 (50-a-b)枚(即0<=c<=50-a-b)。采用这种思路优化后的源程序如下。
#include <stdio.h>
int main()
{
int a,b,c,d,cnt=0;
for(a=0;a<=20;a++)
for(b=0;b<=50-a;b++)
for(c=0;c<=50-a-b;c++)
{
d=50-a-b-c; // 剩下的用5分硬币填充
if(100*a+50*b+10*c+5*d==2000)
{
printf("%d: %d , %d , %d , %d ",++cnt,a,b,c,d);
}
}
return 0;
}
9-2 和积三角形
问题描述
把和为正整数s的8个互不相等的正整数填入8数字三角形(如图1所示)中,若三角形三边上的数字之和相等且三边上的数字之积也相等,该三角形称为和积三角形。
图1 数字三角形
例如,和为45的和积三角形如图2所示。
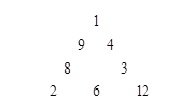
图2 s=45的和积三角形
编写一个程序,输出和为s的和积三角形。
输入数据
一个正整数S(36≤S≤300)。
输出要求
所有和为S的和积三角形,要求输出的方案不重复。如图2中,8和9交换,或4和3交换,或同时交换9与4、8和3、2和12,所得到的3种方案均视为与图2给出的方案是同一种方案。
输入样例
45
输出样例
1:2 , 8 , 9 , 1 , 4 , 3 , 12 , 6 , s1=20, s2=144
说明
对照图2的数据,注意体会样例中8个数的输出顺序,另外是s1的值代表各边上整数的和,s2的值代表各边上整数的积。
(1)编程思路。
按输出样例的说明,设图1所示的数字三角形的8个数分布如下图3所示。
因为三角形的两个腰可以互相交换,为避免重复,不妨约定三角形中数字“下小上大、左小右大”,即 b1<b7、b2<b3且b6<b5。

图3 三角形分布示意图
这样,可以根据约定对b1、b7的值进行循环探索,设置:
b1的取值范围为1 ~ (s-21)/2; (因除b1、b7外,其他6个数之和至少为21)
b7的取值范围为b1+1 ~ (s-28); (因除b7外,其他7个数之和至少为28)
b4的取值范围为1 ~ (s-28); (因除b4外,其他7个数之和至少为28)
同理,根据约定b2<b3,b6<b5,可设置:
b2 的取值范围为1 ~ (s-21)/2; (因除b2、b3外,其他6个数之和至少为21)
b3 的取值范围为b2+1 ~ (s-28);
b6 的取值范围为1 ~ (s-21)/2; (因除b5、b6外,其他6个数之和至少为21)
b5 的取值范围为b(6)+1 ~ (s-28);
b8 = s-(b1+b2+b3+b4+b5+b6+b7)
对所取的8个整数,需要进行以下4道检测:
1)若b8<=0,则不符合要求;
2)若这8个数出现相同数,则不符合要求;
3)若三边之和不等,则不符合要求;
4)若三边之积不等,则不符合要求。
若某8个数通过以上4道检测,即为一个解,打印输出,并统计解的个数。
由于需要对8个整数中是否出现相同数进行检测,因此可以将8个数保存在一个一维数组中,定义一维数组 int b[9];其中数组元素b[1] ~ b[8]分别对应图3中的b1 ~ b8。
程序总体可以写成一个七重循环结构,如下:
for(b[1]=1;b[1]<=(s-21)/2;b[1]++)
for(b[7]=b[1]+1;b[7]<=s-28;b[7]++)
for(b[4]=1;b[4]<=s-28;b[4]++)
for(b[2]=1;b[2]<=(s-21)/2;b[2]++)
for(b[3]=b[2]+1;b[3]<=s-28;b[3]++)
for(b[6]=1;b[6]<=(s-21)/2;b[6]++)
for(b[5]=b[6]+1;b[5]<=s-28;b[5]++)
{
根据穷举的8个数,进行4道检测,确定是否为一组解;
}
4道检测中,除检查8个数中是否出现相同数复杂点外,其他均是简单计算并判断即可。
为检测8个数中是否出现相同的数,可以先设定一个标志 t=0;然后用循环依次将每个数与其后的每个数进行比较,若出现相同,则置t=1并退出循环。
循环执行结束后,若 t==1,则说明8个数中出现了相同的数;若 t保持初始设定值0,则说明8个数中不存在相同的数。算法描述为:
t=0;
for(i=1;i<=7;i++)
for(j=i+1;j<=8;j++)
if(b[i]==b[j])
{
t=1; i=7; break;
}
(2)源程序1。
#include <stdio.h>
int main()
{
int i,j,t,s,s1,s2,cnt,b[9];
scanf("%d",&s);
cnt=0;
for(b[1]=1;b[1]<=(s-21)/2;b[1]++)
for(b[7]=b[1]+1;b[7]<=s-28;b[7]++)
for(b[4]=1;b[4]<=s-28;b[4]++)
for(b[2]=1;b[2]<=(s-21)/2;b[2]++)
for(b[3]=b[2]+1;b[3]<=s-28;b[3]++)
for(b[6]=1;b[6]<=(s-21)/2;b[6]++)
for(b[5]=b[6]+1;b[5]<=s-28;b[5]++)
{
b[8]= s-(b[1]+b[2]+b[3]+b[4]+b[5]+b[6]+b[7]);
if(b[8]<=0) continue;
t=0;
for(i=1;i<=7;i++)
for(j=i+1;j<=8;j++)
if(b[i]==b[j])
{ t=1; i=7; break; }
if(t==1) continue;
s1= b[1]+b[2]+b[3]+b[4];
if(b[4]+b[5]+b[6]+b[7]!=s1 || b[1]+b[8]+b[7]!=s1)
continue;
s2=b[1]*b[2]*b[3]*b[4];
if(b[4]*b[5]*b[6]*b[7]!=s2 || b[1]*b[8]*b[7]!=s2)
continue;
cnt++;
printf("%d : ",cnt);
for(i=1; i<=8; i++)
printf("%d , ",b[i]);
printf(" s1=%d, s2=%d ",s1,s2);
}
return 0;
}
(3)穷举优化思路。
上面的穷举程序设计虽然可行。但是,这个程序的运行速度太慢。例如将程序中的s=45改成s=89,即计算和为89的8个整数组成的和积三角形,程序运行后,可得到如下所示的结果。
1 : 6 , 14 , 18 , 1 , 9 , 8 , 21 , 12 , s1=39, s2=1512
2 : 8 , 12 , 15 , 1 , 16 , 9 , 10 , 18 , s1=36, s2=1440
3 : 8 , 4 , 27 , 2 , 12 , 3 , 24 , 9 , s1=41, s2=1728
4 : 15 , 9 , 16 , 1 , 12 , 10 , 18 , 8 , s1=41, s2=2160
程序得到以上4个解需等待较长时间。为了提高求解效率,必须对程序进行优化,可以从循环设置入手。具体思路为:
1)增加s+b1+b7+b4是否为3的倍数检测。
因为三角形三个顶点的元素在计算三边时各计算了两次,即s+b1+b7+b4=3*s1,则在b1、b4、b7循环中增加对s+b1+b7+b4是否能被3整除的检测。
若(s+b1+b7+b4)%3≠0,则直接continue,继续新的b1、b4、b7探索,而无需探索后面的b2、b3、b5和b6;
否则,记s1=(s+b1+b7+b4)/3,往下进行探索。
2)精简循环,把七重循环精简为五重。
保留根据约定对b1、b7和b4的值进行的循环探索,设置同前。优化对b2、b3、b5和b6的循环探索。可根据约定对b3、b5的值进行探索,设置:
b3的取值范围为(s1-b1-b4)/2+1 ~ s1-b1-b4; 注: s1=(s+b1+b7+b4)/3
b5的取值范围为(s1-b4-b7)/2+1 ~ s1-b4-b7;
同时根据各边之和为s1,计算出b2、b6和b8,即
b2=s1-b1-b4-b3
b6=s1-b4-b5-b7
b8=s1-b1-b7
这样,还同时精简了关于b8是否为正的检测,也精简了三边和是否相等的检测。只需检测b数组是否存在相同正整数与三边积是否相同即可。
(4)改进后的源程序。
#include <stdio.h>
int main()
{
int i,j,t,s,s1,s2,cnt,b[9];
scanf("%d",&s);
cnt=0;
for(b[1]=1;b[1]<=(s-21)/2;b[1]++)
for(b[7]=b[1]+1;b[7]<=s-28;b[7]++)
for(b[4]=1;b[4]<=s-28;b[4]++)
{
if((s+b[1]+b[4]+b[7])%3!=0)
continue;
s1=(s+b[1]+b[4]+b[7])/3;
for(b[3]=(s1-b[1]-b[4])/2+1;b[3]<s1-b[1]-b[4];b[3]++)
for(b[5]=(s1-b[4]-b[7])/2+1;b[5]<s1-b[4]-b[7];b[5]++)
{
b[2]=s1-b[1]-b[4]-b[3];
b[6]=s1-b[4]-b[7]-b[5];
b[8]=s1-b[1]-b[7];
t=0;
for (i=1; i<=7; i++)
for(j=i+1;j<=8;j++)
if(b[i]==b[j])
{ t=1; i=7; break; }
if(t==1) continue;
s2=b[1]*b[2]*b[3]*b[4];
if(b[4]*b[5]*b[6]*b[7]!=s2 || b[1]*b[8]*b[7]!=s2)
continue;
cnt++;
printf("%d : ",cnt);
for(i=1; i<=8; i++)
printf("%d , ",b[i]);
printf(" s1=%d, s2=%d ",s1,s2);
}
}
return 0;
}
运行以上改进穷举的程序,当s=89时所得解与前相同,但时间大大缩短。
9-3 完美运算式
问题描述
把数字1、2、…、9这9个数字填入以下含加减乘除与乘方的综合运算式中的9个□中,使得该式成立
□^□+□□÷□□-□□×□=0
要求数字1,2,…、9这9个数字在式中都出现一次且只出现一次。
输入数据
无
输出要求
输出所有可能的填写方式,输出格式见输出样例。
输入样例
无
输出样例
1:3 ^ 5 + 87 / 29 - 41 * 6=0
……
(1)编程思路1。
设式中的6个整数从左至右分别为 a、b、x、y、z、c,其中x、y、z为2位整数,范围为12~98;a、b、c为一位整数,范围为1~9。
设置a、b、c、x、y、z循环,对穷举的每一组a、b、c、x、y、z,进行以下检测:
1)若x不是y的倍数,即 x % y!=0,则返回继续下一次穷举。
2)若等式不成立,即a^b+x/y-z*c!=0,则返回继续下一次穷举。
3)式中9个数字是否存在相同数字。将式中6个整数共9个数字进行分离,分别赋值给数组元素f[1]~f[9]。连同附加的f[0]=0(为保证9个数字均不为0),共10个数字在二重循环中逐个比较。
若存在相同数字,t=1,不是解,继续下一次穷举。
若不存在相同数字,即式中9个数字为1~9不重复,保持标记t=0, 是一组解,输出所得的完美运算式。并统计解的个数 n 。
(2)源程序1。
#include <stdio.h>
int main()
{
int a,b,c,x,y,z;
int i,j,k,t,n,f[10];
n=0;
for(a=1;a<=9;a++)
for(b=1;b<=9;b++)
for(c=1;c<=9;c++)
for(x=12;x<=98;x++)
for(y=12;y<=98;y++)
for(z=12;z<=98;z++)
{
if (x%y!=0) continue;
k=1;
for (i=1;i<=b;i++) // 计算k=a^b
k=a*k;
if(k+x/y-z*c!=0) continue;
f[0]=0;
f[1]=a;f[2]=b;f[3]=c; // 9数字个赋给f数组
f[4]=x/10; f[5]=x%10;
f[6]=y/10; f[7]=y%10;
f[8]=z/10; f[9]=z%10;
t=0;
for(i=0;i<=8;i++)
for(j=i+1;j<=9;j++)
if(f[i]==f[j])
{ t=1; break; } // 检验数字是否有重复
if(t==0)
{
n++; // 输出一个解,用n统计个数
printf("%d:%d ^ %d + %d / %d - %d * %d=0 ",n,a,b,x,y,z,c);
}
}
return 0;
}
(3)编程思路2。
对上面的程序进行优化。
由于要求的综合运算式为:a^b+x/y-z*c=0,那么,x=(z*c-a^b)*y。因此可设置a、b、c、y、z循环,对穷举的每一组a、b、c、y、z,计算x。这样处理,可省略x循环,同时省略x是否能被y整除,省略等式是否成立的检测。
计算x后,只要检测x是否为二位数即可。若计算所得x不是二位整数,则返回继续下一次穷举。
另外,式中9个数字是否存在相同数字可采用这样的方法:
定义f数组对6个整数分离出的9个数字的出现次数进行统计,即f[i]的值为式中数字i的个数,初值全赋值为0。统计后,若某一f[i](i=1~9)不为1,则一定不满足数字1、2、…、9这九个数字都出现一次且只出现一次,标记t=1,不是解,返回继续下一次穷举;若所有f[i]全为1,满足数字1、2、…、9这九个数字都出现一次且只出现一次,保持标记t=0,是解,输出所得的完美综合运算式。
(4)源程序2。
#include <stdio.h>
int main()
{
int a,b,c,x,y,z;
int i,k,t,n,f[10];
n=0;
for(a=1;a<=9;a++)
for(b=1;b<=9;b++)
for(c=1;c<=9;c++)
for(y=12;y<=98;y++)
for(z=12;z<=98;z++)
{
k=1;
for (i=1;i<=b;i++)
k=a*k;
x=(z*c-k)*y;
if(x<10 || x>98) continue;
for(i=1;i<=9;i++)
f[i]=0;
f[a]++; f[b]++; f[c]++; // 记录9个数字各自出现的次数
f[x/10]++; f[x%10]++; f[y/10]++; f[y%10]++;
f[z/10]++; f[z%10]++;
t=0;
for(i=1;i<=9;i++)
if(f[i]!=1)
{ t=1; break; } // 检验数字是否有重复
if(t==0)
{
n++;
printf("%d:%d ^ %d + %d / %d - %d * %d=0 ",n,a,b,x,y,z,c);
}
}
return 0;
}