题目
点这里看题目。
分析
本题的正确解法
看到 (P) 序列的构造方法,我们不难想到将它和树联系起来。
将 (P) 中的 -1 修改为 0 ,并且对于 (i) ,连接边 ((P_i,i)) ,我们就得到了一棵以 0 为根的树,且原序列就是这棵树的一种兄弟节点按照 (H) 不降排序的 DFS 序的结果。
考虑到 DFS 序中区间就对应了子树,且根总是最先遍历,因而我们可以考虑区间 DP 。不过我们还需要处理 (X) 的限制。
注意到我们最终要求的其实是 (P) 序列的本质不同的个数。这就意味着,我们只要能找到一种方法,使得可以构造出来 (H) 序列,且能与 (P) 一一对应即可。考虑到 (X) 限制了上界,因此我们应该让 (P_i) 对应的 (H_i) 尽量地小,这样就可以构造出尽可能多的 (P) 。
那么设 (u) 的子节点集合为 (son(u)) ,在 DFS 序上 (u) 的前一个兄弟节点为 (w) ,我们可以得到 (H_u=max{H_w,max_{vin son(u)}{H_v}+1}) ,此时的 (H) 就是关于当前的 (P) 构造出来的最小的 (H) 。
这就告诉我们,实际操作中, (max{H}le n+1) 。因此我们可以考虑设定状态为:
(f(i,j,k)):区间 ([i,j]) 构造出以 (i) 为根的子树,且 (H_i=k) 的 (P) 的数量。
转移便是考虑给 ([i,j]) 在末尾新添加一棵子树。第一种情况,子树太大,导致 (H_i) 变大:
另一种情况是,新加入的子树的 (H) 本没有路比较小,走的人多了它前面的兄弟的 (H) 太大了,导致它的 (H) 变大了也便成了路:
转移中多次出现了 (sum_{t<k}f(p,j,t)) 这种形式,因此使用前缀和优化,总时间便是 (O(n^4)) 。
本题的另一解法
同样是考虑一段区间如何计算 (P) 。不难发现,将其中 -1 的位置抽取出来后,其 (H) 一定是单调不降的。对于剩余的部分,它们的最大值也就被限制了,相当于同时对某个数取了 (min) 。
具体而言,我们可以对于区间 ([l,r]) ,枚举它最后一个区间的最大值在哪里:
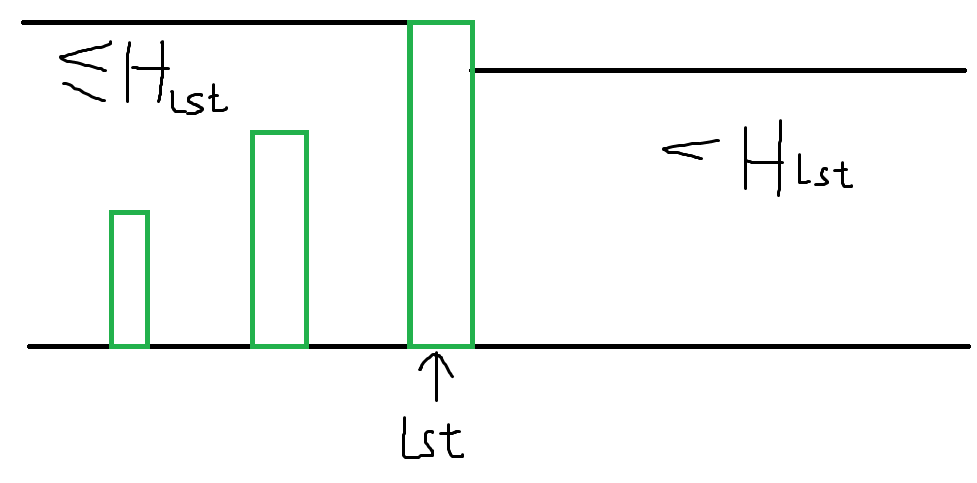
于是,在它之前的值都必须 (le H_{lst}) ,之后的必须 (< H_{lst}) 。于是我们就得到了相似的子问题,可以开始 DP :
(g(i,j,k)):区间 ([i,j]) 中,每个数的 (H) 都同时满足 (X) 和 (le k) 两个限制的 (P) 的个数。
转移非常之简单:
原以为这个是伪解,结果发现是博主的弱智让它变成了伪解。
此时我们可以调用另一正解的结论,即 (max{H}le n+1) ,所以 (g) 的第三维只有 (n+1) 。时间同样是 (O(n^4)) 。
小结:
- 正解一中,由 (P) 到树的转化是非常常见而有用的。事实上,如果遇到了 " 一一对应 " 的序列,我们都可以尝试这个方向,将它转化为图的问题。
- 正解一中,将 (P) 和 (H) 两个序列以一种特殊映射方法联系起来进行转化也是非常常见而有效的。可以参考 HDU 的 X Number 。一般我们可以考虑贪心来进行映射。
- 正解二中,利用 (H) 的有效上界压缩状态也很用。
它直接把这道题的难度拖低了。
代码
正解一代码
#include <cstdio>
typedef long long LL;
const int mod = 1e9 + 7;
const int MAXN = 105;
template<typename _T>
void read( _T &x )
{
x = 0; char s = getchar(); int f = 1;
while( s < '0' || '9' < s ) { f = 1; if( s == '-' ) f = -1; s = getchar(); }
while( '0' <= s && s <= '9' ) { x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ); s = getchar(); }
x *= f;
}
template<typename _T>
void write( _T x )
{
if( x < 0 ) putchar( '-' ), x = -x;
if( 9 < x ) write( x / 10 );
putchar( x % 10 + '0' );
}
int f[MAXN][MAXN][MAXN],
g[MAXN][MAXN][MAXN];
int X[MAXN];
int N;
int Mul( LL x, int v ) { x *= v; if( x >= mod ) x %= mod; return x; }
int Add( int x, int v ) { return x + v >= mod ? x + v - mod : x + v; }
int main()
{
read( N ), X[1] = ++ N;
for( int i = 2 ; i <= N ; i ++ ) read( X[i] );
for( int i = N ; i ; i -- )
{
f[i][i][1] = 1;
for( int k = 1 ; k <= N ; k ++ )
g[i][i][k] = Add( g[i][i][k - 1], f[i][i][k] );
for( int j = i + 1 ; j <= N ; j ++ )
for( int k = 2 ; k <= N && k <= X[i] ; k ++ )
{
for( int p = i + 1 ; p <= j ; p ++ )
f[i][j][k] = Add( f[i][j][k], Add( Mul( g[i][p - 1][k], f[p][j][k - 1] ),
Mul( f[i][p - 1][k], g[p][j][k - 2] ) * ( X[p] >= k - 1 ) ) );
g[i][j][k] = Add( g[i][j][k - 1], f[i][j][k] );
}
}
write( g[1][N][N] ), putchar( '
' );
return 0;
}
正解二代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int T = 3;
const int mod = 1e9 + 7;
const int MAXN = 105;
template<typename _T>
_T MIN( const _T a, const _T b )
{
return a < b ? a : b;
}
int g[MAXN][MAXN][MAXN * T];
int X[MAXN], pnt[MAXN * T];
int N, tot;
int Mul( LL x, int v ) { x *= v; if( x >= mod ) x %= mod; return x; }
int Add( int x, int v ) { return x + v >= mod ? x + v - mod : x + v; }
int main()
{
scanf( "%d", &N );
for( int i = 1 ; i <= N ; i ++ ) scanf( "%d", &X[i] );
tot = N + 1;
for( int i = N ; i ; i -- )
{
for( int t = 0 ; t <= tot ; t ++ )
g[i][i - 1][t] = g[i + 1][i][t] = 1;
for( int j = i ; j <= N ; j ++ )
for( int p = i ; p <= j ; p ++ )
for( int k = 1 ; k <= tot ; k ++ )
{
int h = MIN( X[p], k );
g[i][j][k] = Add( g[i][j][k], Mul( g[i][p - 1][h], g[p + 1][j][h - 1] ) );
}
}
printf( "%d
", g[1][N][tot] );
return 0;
}