极大极小算法简介

概念

Minimax算法又名极小化极大算法，是一种找出失败的最大可能性中的最小值的算法（即最小化对手的最大得益）。通常以递归形式来实现。
Minimax算法常用于棋类等由两方较量的游戏和程序。该算法是一个零总和算法，即一方要在可选的选项中选择将其优势最大化的选择，另一方则选择令对手优势最小化的一个，其输赢的总和为0（有点像能量守恒，就像本身两个玩家都有1点，最后输家要将他的1点给赢家，但整体上还是总共有2点）。很多棋类游戏可以采取此算法，例如tic-tac-toe。

零和游戏（Zero-sum Game）：意思就是你死我活，一方的胜利代表另一方的失败，比如，象棋，五子棋等。
完全信息（Perfect Information）：玩家知道之前所有的步骤。象棋就是完全信息，因为玩家是交替着落子，且之前的步骤都能在棋盘上体现，但是石头剪子布就不是。这样的游戏通常可以把他们看作一个树状图，把每一种可能性列出来。

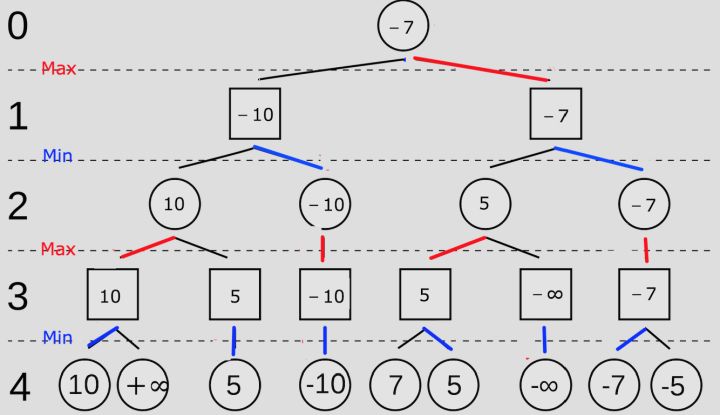
井字棋游戏，Max代表你自己，Min代表你的对手。
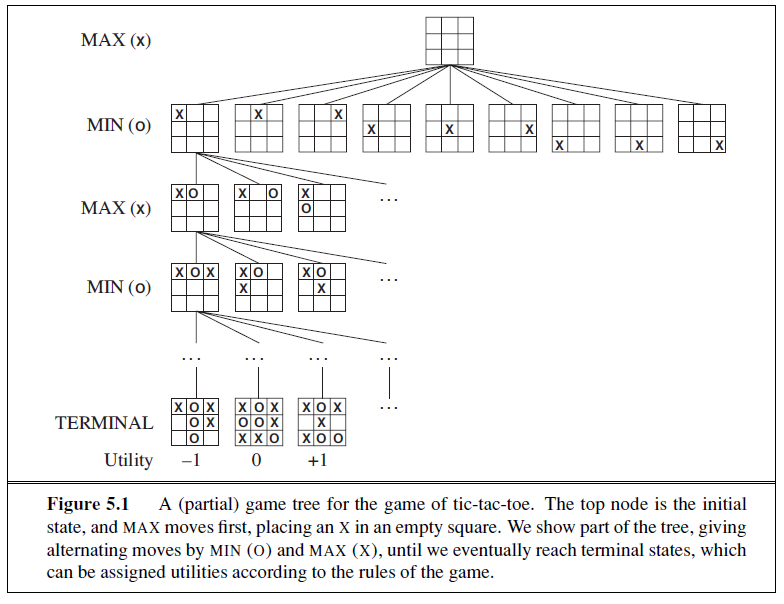
这个时候我们需要给每一种结果一个分数，就是这里的Utility。这个分数是站在我自己（也就是Max）的角度评估的，比如上图中我赢了就是＋1，输了是－1，平局时0。所以，我希望最大化这个分数，而我的对手希望最小化这个分数。（在游戏中，这个分数被称为static value。）
过程：
- 首先，由于双方都采用最优策略行棋，即知道从当前开始到结束的所有棋局状态，再从中选择最有利于自己的棋局，
- 故双方都知道最终的所有棋局状态，因此有下图：
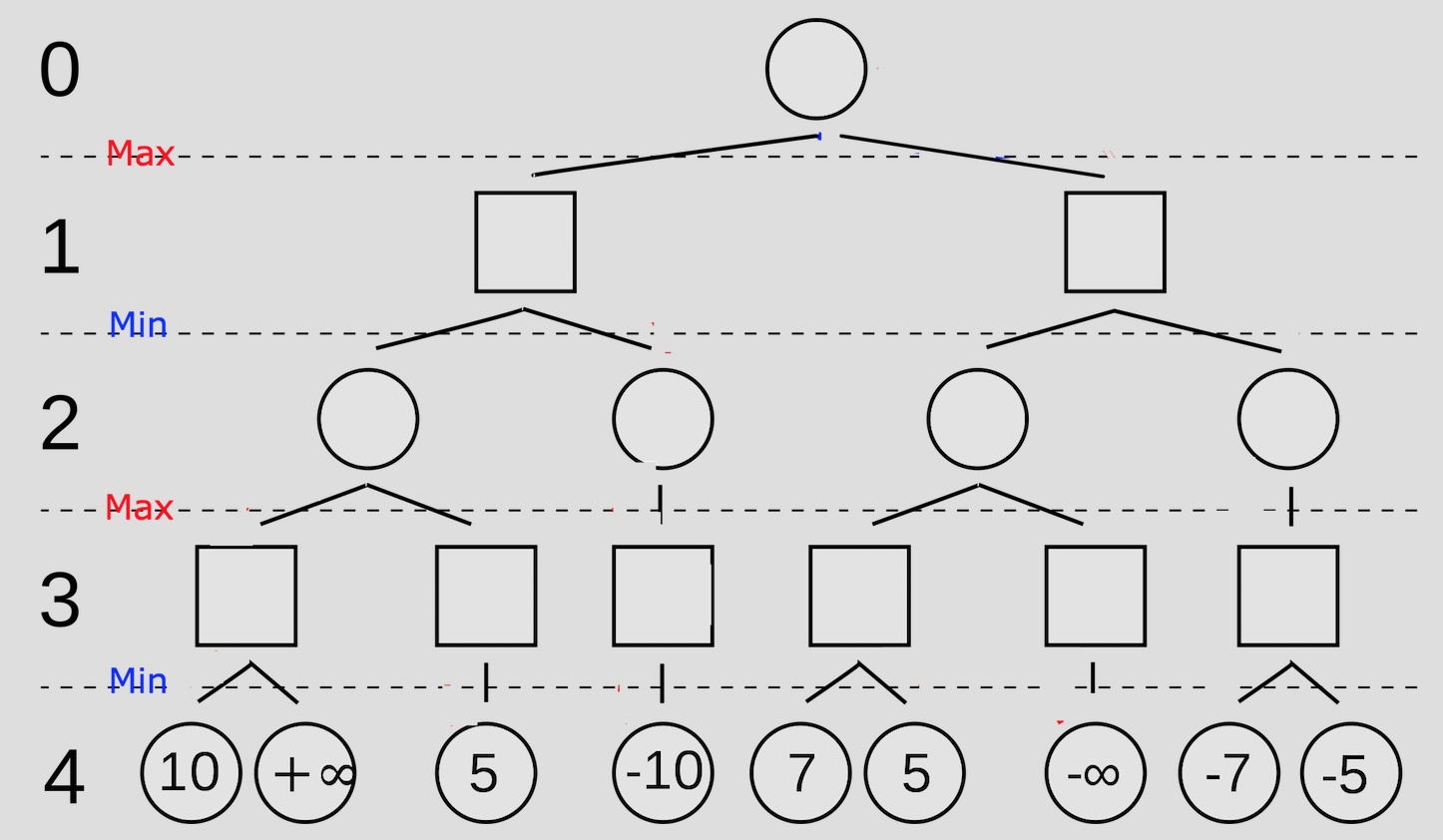
- 从结果看起，也就是第4步。图中标注第四步是我的对手下的，所以他要做的是最小化这个分数，于是对手根据结果可以反推出如下选择
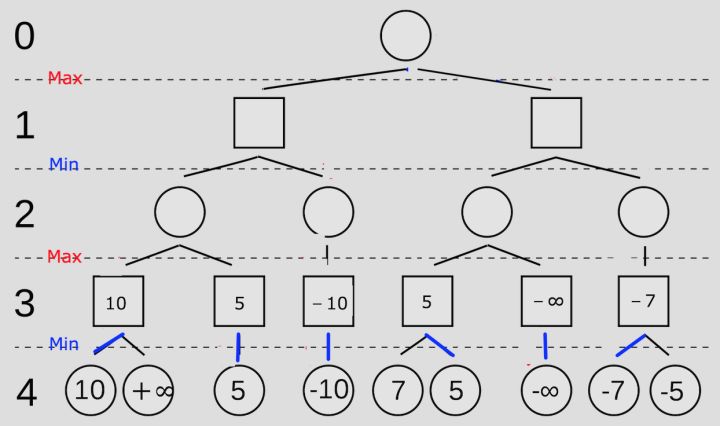
- 从后往前看到第3步，当我们知道了对手的选择以后，我们可以根据对手的结果反推出自己的选择，我们要做的是最大化这个分数，如图
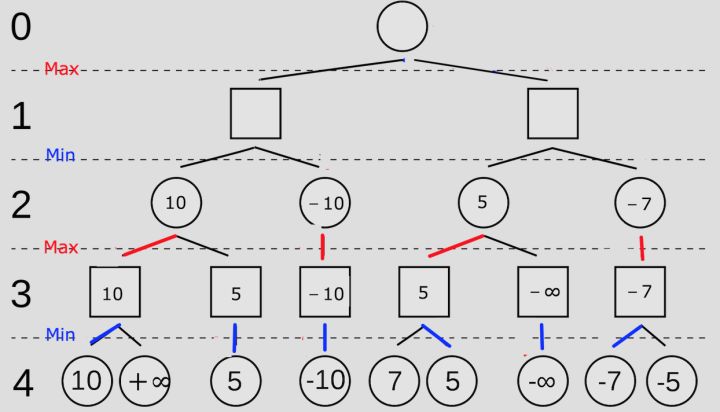
- 我们最终可以发现第一步的最优选择，如图

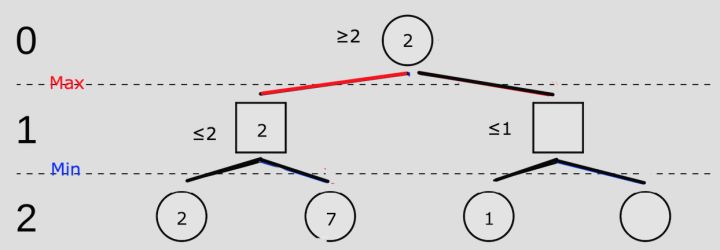
首先将游戏简化如图所示：
但是，最后一步的分数其实也需要计算机来算（static evaluation），所以我们并不会一开始就有所有的数据，其实我们一开始是这样的
然后，计算机给出了第一个分数
当给出了这个分数的时候，我们站在步骤1看，无论另一分支的数字是多少，步骤1左边方框的数字不会超过2。因为第2步是我的对手下的，他希望分数尽可能的小，也就是这样的
这个时候，电脑再计算另一分支的分数，也就是7。知道另一分数是7以后，也就知道步骤1的左边方框分数为2。这时，我们往前看一步（步骤0）。步骤0的分数是大于等于2，因为我要最大化分数。如图
现在，再来计算右边分支的分数，得到了1。同理，我们站在步骤1来看，右边方框中的数不会超过1，如图
在这个情况下，即使我不算最后一个数字，我也能知道在步骤0的结果为2，因为已知步骤1中的右边方框，数值不会超过1。所以我们就能直接知道结果，也就是
们可以看到，加上剪枝算法，我们不仅得到了相同的结果，而且减少了计算量。在实际应用中，加上剪枝算法，计算机大约需要算2*n^{(x/2)个结果，如果n为分支数，x为步数。相比于之前仅用极小极大算法的n}x，效率提高了很多。