Trial Round:
Kwadrat
分解质因数后判断每个质因数的幂是奇数还是偶数,如果是奇数则补成偶数。
时间复杂度$O(\sqrt{n})$。
#include<cstdio>
long long n,ans=1;int i,j;
int main(){
scanf("%lld",&n);
for(i=2;i*i<=n;i++)if(n%i==0){
for(j=0;n%i==0;n/=i,ans*=i)j^=1;
if(j)ans*=i;
}
if(n>1)ans*=n*n;
printf("%lld",ans);
}
Round 1:
Loteria [B]
DP,$f[i][j]$表示考虑了字符串的前$i$位,且第$i$位是字符$j$时所需的最少修改次数,枚举下一位的字符转移。
时间复杂度$O(n)$。
#include<cstdio>
const int N=500010;
int n,i,j,k,f[N][3],ans;char a[N];
inline void up(int&a,int b){a>b?(a=b):0;}
int main(){
scanf("%d%s",&n,a+1);
for(i=1;i<=n;i++)a[i]-='A';
for(i=0;i<=n;i++)for(j=0;j<3;j++)f[i][j]=N;
for(j=0;j<3;j++)f[1][j]=a[1]!=j;
for(i=2;i<=n;i++)for(j=0;j<3;j++)for(k=0;k<3;k++)if(j!=k)up(f[i][j],f[i-1][k]+(j!=a[i]));
ans=N;
for(j=0;j<3;j++)up(ans,f[n][j]);
printf("%d",ans);
}
Round 2:
Jednoręki bandyta [B]
固定第一个排列不动,那么对于第一个排列的每个位置,如果它对答案有贡献,则第二个排列和第三个排列的循环移位方案是确定的,求众数即可。
时间复杂度$O(n\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=300010;
int n,x,i,j,ans;struct E{int a,b,c;}e[N];
inline bool cmp(const E&a,const E&b){return a.b==b.b?a.c<b.c:a.b<b.b;}
int main(){
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&x),e[x].a=i;
for(i=1;i<=n;i++)scanf("%d",&x),e[x].b=i;
for(i=1;i<=n;i++)scanf("%d",&x),e[x].c=i;
for(i=1;i<=n;i++){
e[i].b-=e[i].a;
e[i].b+=n;
e[i].b%=n;
e[i].c-=e[i].a;
e[i].c+=n;
e[i].c%=n;
}
sort(e+1,e+n+1,cmp);
for(i=1;i<=n;i=j){
for(j=i;j<=n&&e[i].b==e[j].b&&e[i].c==e[j].c;j++);
ans=max(ans,j-i);
}
printf("%d",ans);
}
Strajk [A]
对于一个节点,最优的方案是将汇集到该点最晚的列车延误$k$分钟。枚举延误哪个点最晚的列车,然后$O(n+m)$暴力计算答案。
时间复杂度$O(n(n+m))$。
#include<cstdio>
typedef long long ll;
const int N=405,M=80005;
int n,m,K,i,S,x,y,A,B,g[N],v[M],nxt[M],ed,vis[N];ll w[M],p[M],f[N],now,ans;
inline void up(ll&a,ll b){a<b?(a=b):0;}
ll dfs(int x){
if(vis[x])return f[x];
if(x==1)return 0;
vis[x]=1,f[x]=0;
for(int i=g[x];i;i=nxt[i]){
ll tmp=dfs(v[i]);
if(tmp>w[i])now+=tmp-w[i];
up(f[x],tmp+p[i]);
up(f[x],w[i]+p[i]);
}
if(x==S)f[x]+=K;
return f[x];
}
int main(){
scanf("%d%d%d",&n,&m,&K);
while(m--){
scanf("%d%d%d%d",&x,&y,&A,&B);
v[++ed]=x;
w[ed]=A;
p[ed]=B;
nxt[ed]=g[y];
g[y]=ed;
}
for(S=2;S<=n;S++){
for(i=1;i<=n;i++)vis[i]=0;
now=0;
for(i=1;i<=n;i++)dfs(i);
up(ans,now);
}
printf("%lld",ans+K);
}
Round 3:
Karty [A]
显然只需要考虑与障碍点相邻的格子,通过旋转坐标系,可以只考虑障碍点在格子上方的情况。
悬线法求出每个点往上的最长延伸距离$x$,以及往左往右的延伸距离$y$。
那么当$r\geq x$时,$c$至多为$y$。
特别地,当某个点下方也是障碍点的时候,$r$不能超过$x$。
维护出每个$r$对应的最大的$c$即可。
时间复杂度$O(nm)$。
#include<cstdio>
#include<algorithm>
const int N=2505;
int n,m,i,j,k,l[N],r[N],h[N],f[N],ans,pos;char a[N][N],b[N][N];
inline void up(int&a,int b){a>b?(a=b):0;}
void work(int n,int m,int rev){
int i,j,k,x,y;
for(i=1;i<=m;i++)l[i]=1,r[i]=m,h[i]=0,a[n+1][j]='_';
for(i=1;i<=n;i++){
for(j=k=1;j<=m;j++)if(a[i][j]=='X'){
h[j]++;
if(k>l[j])l[j]=k;
}else h[j]=0,l[j]=1,r[j]=m,k=j+1;
for(j=k=m;j;j--)if(a[i][j]=='X'){
up(r[j],k);
x=h[j],y=r[j]-l[j]+1;
if(rev){
up(f[y+1],x-1);
if(a[i+1][j]=='_')up(f[1],x);
}else{
up(f[x],y);
if(a[i+1][j]=='_')f[x+1]=0;
}
}else k=j-1;
}
}
int main(){
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%s",a[i]+1),f[i]=m;
for(i=0;i<4;i++){
work(n,m,i&1);
for(j=1;j<=n;j++)for(k=1;k<=m;k++)b[k][n-j+1]=a[j][k];
std::swap(n,m);
for(j=1;j<=n;j++)for(k=1;k<=m;k++)a[j][k]=b[j][k];
}
for(i=1;i<=n;i++){
if(i>1)up(f[i],f[i-1]);
if(i*f[i]>ans)ans=i*f[i],pos=i;
}
return printf("%d %d",pos,ans/pos),0;
}
Panorama Bajhattanu [B]
将两个数组都从小到大排序,则格子$(i,j)$的高度最大可以取到$\min(a[i],b[j])$,且有解的条件是$\max(a)=\max(b)$。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1000010;
int n,m,i,j,x,a[N],b[N],ma,mb;long long ans;
int main(){
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++)scanf("%d",&x),a[x]++,ma=max(ma,x);
for(i=1;i<=m;i++)scanf("%d",&x),b[x]++,mb=max(mb,x);
if(ma!=mb)return puts("NIE"),0;
for(i=ma;i;i--)a[i-1]+=a[i],b[i-1]+=b[i];
for(i=1;i<=ma;i++)ans+=1LL*a[i]*b[i];
printf("%lld",ans);
}
Round 4:
Iloczyn [B]
首先将$n$的约数从小到大排序,设$dfs(x,y,z)$表示当前可以选第$x$个到第$m$个约数,还要选$y$个,之前选的乘积为$z$是否可能。
爆搜的时候,如果从$x$开始最小的$y$个相乘也超过了$n$,那么就不合法,加上这个剪枝即可。
#include<cstdio>
#include<algorithm>
#define N 2000
int T,n,k,m,i,j,q[N],f[N][22];
int dfs(int x,int y,int z){
if(!y)return z==n;
for(y--;x+y<=m;x++){
if(f[x][y]<0)return 0;
if(1LL*f[x][y]*z>n)return 0;
if(dfs(x+1,y,z*q[x]))return 1;
}
return 0;
}
int main(){
scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&k);
for(m=0,i=1;i*i<=n;i++)if(n%i==0){
q[++m]=i;
if(i*i!=n)q[++m]=n/i;
}
std::sort(q+1,q+m+1);
for(i=1;i<=m;i++){
long long t=1;
for(j=0;j<k&&i+j<=m;f[i][j++]=t)if(t>0){
t*=q[i+j];
if(t>n)t=-1;
}
}
puts(dfs(1,k,1)?"TAK":"NIE");
}
return 0;
}
Journey [A]
对$[1,n]$所有未访问过的点按编号建立线段树,线段树每个节点维护区间内点集的字典序最大的直径端点,使用ST表支持$O(1)$查询两点树上距离。
时间复杂度$O(n\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=500005,K=20;
int n,i,j,x,y,A,B,g[N],v[N<<1],nxt[N<<1],ed;
int d[N],Log[N<<1],loc[N],dfn,q[K][N<<1];
int pos[N];
inline void add(int x,int y){v[++ed]=y;nxt[ed]=g[x];g[x]=ed;}
void dfs(int x,int y){
d[x]=d[y]+1;
q[0][loc[x]=++dfn]=d[x];
for(int i=g[x];i;i=nxt[i])if(v[i]!=y){
dfs(v[i],x);
q[0][++dfn]=d[x];
}
}
inline int lca(int x,int y){
x=loc[x],y=loc[y];
if(x>y)swap(x,y);
int k=Log[y-x+1];
return min(q[k][x],q[k][y-(1<<k)+1]);
}
inline int dis(int x,int y){return d[x]+d[y]-lca(x,y)*2;}
struct P{
int a,b;
P(){}
P(int _a,int _b){a=_a,b=_b;}
void add(int x){
int pre=dis(a,b);
int now=dis(x,a);
int na=a,nb=b;
if(now>pre||now==pre&&x+a>na+nb)pre=now,na=a,nb=x;
now=dis(x,b);
if(now>pre||now==pre&&x+b>na+nb)na=b,nb=x;
a=na,b=nb;
}
P operator+(const P&Q)const{
if(!a)return Q;
if(!Q.a)return*this;
P t=*this;
t.add(Q.a);
t.add(Q.b);
return t;
}
}val[1111111];
void build(int x,int a,int b){
if(a==b){
val[x]=P(a,a);
pos[a]=x;
return;
}
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
val[x]=val[x<<1]+val[x<<1|1];
}
inline void del(int x){
x=pos[x];
val[x]=P(0,0);
for(x>>=1;x;x>>=1)val[x]=val[x<<1]+val[x<<1|1];
}
int main(){
scanf("%d",&n);
for(i=1;i<n;i++)scanf("%d%d",&x,&y),add(x,y),add(y,x);
dfs(1,0);
for(i=2;i<=dfn;i++)Log[i]=Log[i>>1]+1;
for(i=1;i<K;i++)for(j=1;j+(1<<i)-1<=dfn;j++)q[i][j]=min(q[i-1][j],q[i-1][j+(1<<(i-1))]);
build(1,1,n);
for(i=B=1;i<=n;i++){
if(i>1){
B=val[1].a;
int tmp=dis(A,val[1].b)-dis(A,B);
if(tmp>0||tmp==0&&val[1].b>B)B=val[1].b;
}
printf("%d%c",A=B,i<n?' ':'\n');
del(A);
}
}
Round 5:
Konduktorzy [B]
二分一个最大的位置$x$,计算$t=\sum_{i=1}^k\lfloor\frac{x}{a_i}\rfloor$。
如果$t\leq n$,那么说明就算全部检票员都走到了这里,也不够$n$个指令,所以可以先将所有检票员尽量向$x$位置走,并将用掉的指令数扣除。
然后将$x$适当往前调整,使得每个检票员还差至少一步。
因为$a_i$互不相同,并且$a_i\leq 100000$,所以剩余指令数并不多,用堆直接模拟即可。
时间复杂度$O(k\log^2k)$。
#include<cstdio>
#include<algorithm>
#include<queue>
#define N 100010
using namespace std;
typedef long long ll;
typedef pair<ll,int> P;
int n,i,a[N];ll m,L,R,mid,fin,now,ans[N];priority_queue<P,vector<P>,greater<P> >Q;
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
bool check(ll x){
ll t=m;
for(int i=1;i<=n;i++){
t-=x/a[i];
if(t<0)return 0;
}
return 1;
}
int main(){
scanf("%lld",&m);read(n);
for(i=1;i<=n;i++){
read(a[i]);
if(a[i]>R)R=a[i];
}
L=R+1,R*=m;
while(L<=R)if(check(mid=(L+R)>>1))L=(fin=mid)+1;else R=mid-1;
for(R=fin,i=1;i<=n;i++)R=min(R,max((fin/a[i]-1)*a[i],0LL));
for(i=1;i<=n;i++)now+=R/a[i],Q.push(P(R/a[i]*a[i],i));
while(now<m){
P t=Q.top();Q.pop();
ans[t.second]=++now;
t.first+=a[t.second];
Q.push(t);
}
for(i=1;i<n;i++)printf("%lld ",ans[i]);printf("%lld",ans[n]);
return 0;
}
Mutacje [B]
对于每个询问:
- 如果两个子串完全匹配,则答案是TAK。
- 否则通过LCP找到从左往右第一个失配位$(a,b)$,判断所有$a$变成$b$后是否匹配,可以用Hash完成。
时间复杂度$O(q\log n)$。
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int N=500010,P1=1000000007,P2=1000000009,S1=233,S2=13331;
int q,i,w1[N],w2[N],p1[N],p2[N];
struct DS{
int n,i,x,y,a[N],s1[N],s2[N],f1[N],f2[N],last[N],pre[N];
vector<int>g[N];
void init(){
scanf("%d",&n);
for(i=1;i<=n;i++){
scanf("%d",&x);
a[i]=x;
g[x].push_back(i);
pre[i]=y=last[x];
last[x]=i;
s1[i]=(1LL*s1[y]*p1[i-y]+1)%P1;
s2[i]=(1LL*s2[y]*p2[i-y]+1)%P2;
f1[i]=(1LL*f1[i-1]*p1[1]+w1[x])%P1;
f2[i]=(1LL*f2[i-1]*p2[1]+w2[x])%P2;
}
}
int ask1(int l,int r){
return ((f1[r]-1LL*f1[l-1]*p1[r-l+1])%P1+P1)%P1;
}
int ask2(int l,int r){
return ((f2[r]-1LL*f2[l-1]*p2[r-l+1])%P2+P2)%P2;
}
}A,B;
inline bool query(){
int a,b,len;
scanf("%d%d%d",&a,&b,&len);
int F1=A.ask1(a,a+len-1),F2=A.ask2(a,a+len-1),G1=B.ask1(b,b+len-1),G2=B.ask2(b,b+len-1);
if(F1==G1&&F2==G2)return 1;
int l=1,r=len,mid,lcp=0;
while(l<=r){
mid=(l+r)>>1;
if(A.ask1(a,a+mid-1)==B.ask1(b,b+mid-1)&&A.ask2(a,a+mid-1)==B.ask2(b,b+mid-1))l=(lcp=mid)+1;else r=mid-1;
}
int s=A.a[a+lcp],t=B.a[b+lcp];
//s->t
//printf("s=%d t=%d\n",s,t);
int st=*lower_bound(A.g[s].begin(),A.g[s].end(),a),en=*(lower_bound(A.g[s].begin(),A.g[s].end(),a+len)-1),pre=A.pre[st];
//printf("st=%d en=%d pre=%d\n",st,en,pre);
int base=1LL*(((A.s1[en]-1LL*A.s1[pre]*p1[en-pre])%P1+P1)%P1)*p1[a+len-1-en]%P1;
if(((F1+1LL*(w1[t]-w1[s])*base)%P1+P1)%P1!=G1)return 0;
base=1LL*(((A.s2[en]-1LL*A.s2[pre]*p2[en-pre])%P2+P2)%P2)*p2[a+len-1-en]%P2;
if(((F2+1LL*(w2[t]-w2[s])*base)%P2+P2)%P2!=G2)return 0;
return 1;
}
int main(){
for(p1[0]=p2[0]=i=1;i<N;i++){
w1[i]=(19971123LL*w1[i-1]+20200908)%P1;
w2[i]=(3071LL*w2[i-1]+19260817)%P2;
p1[i]=1LL*p1[i-1]*S1%P1;
p2[i]=1LL*p2[i-1]*S2%P2;
}
A.init();
B.init();
scanf("%d",&q);
while(q--)puts(query()?"TAK":"NIE");
}
Raper [A]
将选取的$A$看成左括号,$B$看成右括号,那么答案是一个合法的括号序列。
那么只要重复取出$k$对价值最小的左右括号,保证每时每刻都是一个合法的括号序列即可。
将$($看成$1$,$)$看成$-1$,设$s[]$为前缀和。
如果当前取出的是$()$,那么对前缀和的影响为$[A,B-1]$区间加$1$。
如果当前取出的是$)($,那么对前缀和的影响为$[B,A-1]$区间减$1$,所以这种情况需要满足区间$s$的最小值不为$0$。
考虑用线段树维护这个序列,线段树上每个节点维护以下信息:
va:$A\leq B$情况的最优解。
vb:$A>B$情况的最优解,且满足$[A,B-1]$的区间$s$最小值大于当前区间的$s$最小值。
vc:$A>B$情况的最优解。
aa:区间内代价最小的$A$。
ab:区间内代价最小的$B$。
ba:区间内代价最小的$A$,满足$[st,A-1]$的区间$s$最小值大于区间$s$最小值。
bb:区间内代价最小的$B$,满足$[B,en]$的区间$s$最小值大于区间$s$最小值。
vm:区间$s$最小值。
tag:区间增量标记。
为了方便维护,可以考虑增加第$0$项,$A[0]=B[0]=+\infty$。
那么$[0,n]$区间的$vb$必定满足区间最小值不为$0$,然后贪心选取$k$次即可求出最优解。
时间复杂度$O(k\log n)$。
#include<cstdio>
const int N=500010,M=1050000,inf=1000000010;
long long ans;
int n,k,i,j,A[N],B[N],aa[M],ab[M],ba[M],bb[M],vm[M],tag[M];
struct P{
int x,y;
P(){}
P(int _x,int _y){x=_x,y=_y;}
P operator+(const P&b){return A[x]+B[y]<A[b.x]+B[b.y]?*this:b;}
}va[M],vb[M],vc[M],t;
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
inline void add1(int x,int p){vm[x]+=p;tag[x]+=p;}
inline void pb(int x){if(tag[x])add1(x<<1,tag[x]),add1(x<<1|1,tag[x]),tag[x]=0;}
inline void up(int x){
int l=x<<1,r=l|1;
va[x]=va[l]+va[r]+P(aa[l],ab[r]);
vc[x]=vc[l]+vc[r]+P(aa[r],ab[l]);
vb[x]=vb[l]+vb[r];
aa[x]=A[aa[l]]<A[aa[r]]?aa[l]:aa[r];
ab[x]=B[ab[l]]<B[ab[r]]?ab[l]:ab[r];
if(vm[l]<vm[r]){
vb[x]=vb[x]+vc[r]+P(aa[r],bb[l]);
ba[x]=ba[l];
bb[x]=B[ab[r]]<B[bb[l]]?ab[r]:bb[l];
vm[x]=vm[l];
}
if(vm[l]>vm[r]){
vb[x]=vb[x]+vc[l]+P(ba[r],ab[l]);
ba[x]=A[aa[l]]<A[ba[r]]?aa[l]:ba[r];
bb[x]=bb[r];
vm[x]=vm[r];
}
if(vm[l]==vm[r]){
vb[x]=vb[x]+P(ba[r],bb[l]);
ba[x]=ba[l];
bb[x]=bb[r];
vm[x]=vm[l];
}
}
void build(int x,int a,int b){
if(a==b){
va[x]=vc[x]=P(a,a),vb[x]=P(0,0);
aa[x]=ab[x]=ba[x]=a;
return;
}
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b),up(x);
}
void add(int x,int a,int b,int c,int d,int p){
if(c<=a&&b<=d){add1(x,p);return;}
pb(x);
int mid=(a+b)>>1;
if(c<=mid)add(x<<1,a,mid,c,d,p);
if(d>mid)add(x<<1|1,mid+1,b,c,d,p);
up(x);
}
void change(int x,int a,int b,int c){
if(a==b)return;
pb(x);
int mid=(a+b)>>1;
if(c<=mid)change(x<<1,a,mid,c);else change(x<<1|1,mid+1,b,c);
up(x);
}
int main(){
read(n),read(k);
for(i=1;i<=n;i++)read(A[i]);
for(i=1;i<=n;i++)read(B[i]);
A[0]=B[0]=inf;
build(1,0,n);
while(k--){
t=va[1]+vb[1],i=t.x,j=t.y,ans+=A[i]+B[j];
if(i<j)add(1,0,n,i,j-1,1);
if(i>j)add(1,0,n,j,i-1,-1);
A[i]=inf,change(1,0,n,i);
B[j]=inf,change(1,0,n,j);
}
return printf("%lld",ans),0;
}
Round 6:
Działka [B]
对于每个询问,首先可以通过扫描线+线段树求出四个方向的第一个点,询问范围等价于框住这些点的最小矩形。
对于一个点$i$,预处理出:
$A[i][j]$:$i$往左下角按凸壳走到$j$时,凸壳上相邻两点的叉积和。
$B[i][j]$:$i$往右下角按凸壳走到$j$时,凸壳上相邻两点的叉积和。
$C[i][j]$:$i$往左上角按凸壳走到$j$时,凸壳上相邻两点的叉积和。
$D[i][j]$:$i$往右上角按凸壳走到$j$时,凸壳上相邻两点的叉积和。
注意到每个数组只有一半有用,所以可以把$AD$合并、$BC$合并。
那么答案相当于在$4$个边界点上按凸包走一圈的叉积和再除以二,如下图,这可以$O(1)$计算。
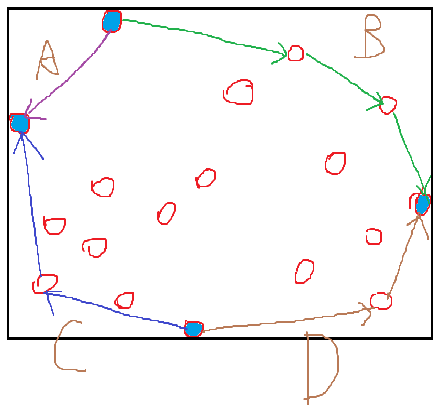
时间复杂度$O(n^2+m\log m)$。
#include<cstdio>
#include<algorithm>
using std::sort;
typedef long long ll;
const int N=3005,M=1000010;
int K,n,m,i,j,k,t,q[N];ll A[N][N],B[N][N],ans;
struct P{
int x,y,p;
inline ll operator*(const P&b){return 1LL*x*b.y-1LL*y*b.x;}
}a[N];
inline bool cmpA(const P&a,const P&b){return a.x==b.x?a.y<b.y:a.x<b.x;}
inline bool cmpB(const P&a,const P&b){return a.x==b.x?a.y>b.y:a.x<b.x;}
inline bool cmpx(const P&a,const P&b){return a.x<b.x;}
inline bool cmpy(const P&a,const P&b){return a.y<b.y;}
struct Q{
int a,b,c,d;
Q(){}
Q(int _a,int _b,int _c,int _d){a=_a,b=_b,c=_c,d=_d;}
}que[M],e[M];
int NA[M],NB[M],NC[M],ND[M];
inline bool cmpE(const Q&a,const Q&b){return a.a<b.a;}
int T[2100000],vis[N],pos;
void build(int x,int a,int b){
T[x]=0;
if(a==b)return;
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
}
void change(int x,int a,int b,int c,int p){
T[x]=p;
if(a==b)return;
int mid=(a+b)>>1;
if(c<=mid)change(x<<1,a,mid,c,p);else change(x<<1|1,mid+1,b,c,p);
}
inline int merge(int x,int y){return vis[x]>vis[y]?x:y;}
int ask(int x,int a,int b,int c,int d){
if(c<=a&&b<=d)return T[x];
int mid=(a+b)>>1,t=0;
if(c<=mid)t=ask(x<<1,a,mid,c,d);
if(d>mid)t=merge(t,ask(x<<1|1,mid+1,b,c,d));
return t;
}
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
int main(){
read(K),read(n);
for(i=1;i<=n;i++)read(a[i].x),read(a[i].y),a[i].p=i;
sort(a+1,a+n+1,cmpA);
for(i=2;i<=n;i++){
k=a[q[t=0]=i].p;
for(j=i-1;j;j--)if(a[j].y<=a[i].y){
while(t&&1LL*(a[q[t-1]].x-a[q[t]].x)*(a[q[t]].y-a[j].y)<1LL*(a[q[t]].x-a[j].x)*(a[q[t-1]].y-a[q[t]].y))t--;
A[k][a[j].p]=A[k][a[q[t]].p]+a[q[t]]*a[j];
q[++t]=j;
}
}
for(i=1;i<n;i++){
k=a[q[t=0]=i].p;
for(j=i+1;j<=n;j++)if(a[j].y>=a[i].y){
while(t&&1LL*(a[q[t]].x-a[q[t-1]].x)*(a[j].y-a[q[t]].y)<1LL*(a[j].x-a[q[t]].x)*(a[q[t]].y-a[q[t-1]].y))t--;
A[k][a[j].p]=A[k][a[q[t]].p]+a[q[t]]*a[j];
q[++t]=j;
}
}
sort(a+1,a+n+1,cmpB);
for(i=1;i<n;i++){
k=a[q[t=0]=i].p;
for(j=i+1;j<=n;j++)if(a[j].y<=a[i].y){
while(t&&1LL*(a[q[t]].x-a[q[t-1]].x)*(a[j].y-a[q[t]].y)>1LL*(a[j].x-a[q[t]].x)*(a[q[t]].y-a[q[t-1]].y))t--;
B[k][a[j].p]=B[k][a[q[t]].p]+a[q[t]]*a[j];
q[++t]=j;
}
}
for(i=2;i<=n;i++){
k=a[q[t=0]=i].p;
for(j=i-1;j;j--)if(a[j].y>=a[i].y){
while(t&&1LL*(a[q[t-1]].x-a[q[t]].x)*(a[q[t]].y-a[j].y)>1LL*(a[q[t]].x-a[j].x)*(a[q[t-1]].y-a[q[t]].y))t--;
B[k][a[j].p]=B[k][a[q[t]].p]+a[q[t]]*a[j];
q[++t]=j;
}
}
read(m);
for(i=1;i<=m;i++)read(que[i].a),read(que[i].b),read(que[i].c),read(que[i].d);
for(i=1;i<=m;i++)e[i]=Q(que[i].d,que[i].a,que[i].b,i);
sort(a+1,a+n+1,cmpy),sort(e+1,e+m+1,cmpE);
for(build(1,0,K),i=j=1;i<=m;i++){
while(j<=n&&a[j].y<=e[i].a)change(1,0,K,a[j].x,a[j].p),vis[a[j].p]=++pos,j++;
NA[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
}
for(i=1;i<=m;i++)e[i]=Q(que[i].c,que[i].a,que[i].b,i);
sort(a+1,a+n+1,cmpy),sort(e+1,e+m+1,cmpE);
for(build(1,0,K),i=m,j=n;i;i--){
while(j&&a[j].y>=e[i].a)change(1,0,K,a[j].x,a[j].p),vis[a[j].p]=++pos,j--;
NC[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
}
for(i=1;i<=m;i++)e[i]=Q(que[i].b,que[i].c,que[i].d,i);
sort(a+1,a+n+1,cmpx),sort(e+1,e+m+1,cmpE);
for(build(1,0,K),i=j=1;i<=m;i++){
while(j<=n&&a[j].x<=e[i].a)change(1,0,K,a[j].y,a[j].p),vis[a[j].p]=++pos,j++;
ND[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
}
for(i=1;i<=m;i++)e[i]=Q(que[i].a,que[i].c,que[i].d,i);
sort(a+1,a+n+1,cmpx),sort(e+1,e+m+1,cmpE);
for(build(1,0,K),i=m,j=n;i;i--){
while(j&&a[j].x>=e[i].a)change(1,0,K,a[j].y,a[j].p),vis[a[j].p]=++pos,j--;
NB[e[i].d]=ask(1,0,K,e[i].b,e[i].c);
}
for(i=1;i<=m;i++){
ans=A[NA[i]][NB[i]]-B[NA[i]][ND[i]]-B[NC[i]][NB[i]]+A[NC[i]][ND[i]];
printf("%lld.%d\n",ans>>1LL,ans&1LL?5:0);
}
return 0;
}
Filary [B]
当$m$取$2$时,$k$至少为$\frac{n}{2}$,所以在最优解中每个数被选中的概率至少为$\frac{1}{2}$。
每次随机选取一个位置$i$,计算出其它数与$a_i$的差值,将差值分解质因数。
所有质因数中出现次数的最大值加上与$a_i$相等的数的个数就是选取$i$的情况下的最优解。
为了最大化$m$,需要将所有相同位置的因数乘起来。
给每个位置随机一个权值,全部异或起来求出Hash值,排序后扫一遍统计即可。
因为$a_i\leq10^7$,所以可以先一遍线性筛求出每个数是被哪个素数筛掉的,这样就可以做到$O(\log a)$分解质因数。
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=100010,P=664600;
int n,i,j,x,a[N],b[N],maxv,p[P],tot,ans1,ans2,T,cnt,pos[P],las[P],now,v[10000001],tmp[32],fac,vis[P];
struct PI{
int cnt,hash,num;
PI(){cnt=hash=0;num=1;}
PI(int _cnt,int _hash,int _num){cnt=_cnt,hash=_hash,num=_num;}
}pool[P];
inline bool cmp(PI a,PI b){return a.hash<b.hash;}
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
inline void divide(int x,int y){
int i,j,k;
for(i=0;i<fac;i++)vis[tmp[i]]=0;
for(fac=0;x^1;vis[v[x]]*=p[v[x]],x/=p[v[x]])if(!vis[v[x]])tmp[fac++]=v[x],vis[v[x]]=1;
for(i=0;i<fac;i++){
k=vis[tmp[i]];
if(las[tmp[i]]^T)las[tmp[i]]=T,pool[j=pos[tmp[i]]=++now]=PI(0,0,k);else j=pos[tmp[i]];
pool[j].cnt++,pool[j].hash^=y;
if(pool[j].num>k)pool[j].num=k;
}
}
int main(){
pool[0].hash=-1;
for(read(n);i<n;i++){
read(a[i]);
while(!b[i])b[i]=rand();
if(a[i]>maxv)maxv=a[i];
}
for(i=2;i<=maxv;i++){
if(!v[i])p[v[i]=++tot]=i;
for(j=1;j<=tot;j++){
if(i*p[j]>maxv)break;
v[i*p[j]]=j;
if(i%p[j]==0)break;
}
}
for(T=1;T<=4;T++){
for(x=a[rand()%n],i=cnt=now=0;i<n;i++)if(a[i]!=x)divide(a[i]>x?(a[i]-x):(x-a[i]),b[i]);else cnt++;
sort(pool+1,pool+now+1,cmp);
for(j=0,i=1;i<=now;i++)if(pool[i].hash^pool[j].hash){
if(j){
if(pool[j].cnt+cnt>ans1)ans1=pool[j].cnt+cnt,ans2=pool[j].num;
else if(pool[j].cnt+cnt==ans1&&pool[j].num>ans2)ans2=pool[j].num;
}
j=i;
}else pool[j].num*=pool[i].num;
if(pool[j].cnt+cnt>ans1)ans1=pool[j].cnt+cnt,ans2=pool[j].num;
else if(pool[j].cnt+cnt==ans1&&pool[j].num>ans2)ans2=pool[j].num;
}
return printf("%d %d",ans1,ans2),0;
}
Kryształ [A]
逆时针考虑每条边:
- 如果是$0\rightarrow 2$,则对答案的贡献为$-1$。
- 如果是$2\rightarrow 0$,则对答案的贡献为$1$。
- 其它所有边对答案无贡献。
根据数据生成方式的循环节计算答案即可。
Mrówki [A]
使用线段树从左往右对于每只蚂蚁维护其坐标$f$以及速度$v$。
线段树上维护4个标记$ta$、$tb$、$tc$、$td$,表示$f'=f+ta\times v+tb$,且$v'=tc\times v+td$,并记录区间内最左和最右的蚂蚁的坐标以及速度。
用堆按时间维护所有可能发生的两类事件:
(1) $t$时刻$x$号水滴落在了地上。
(2) $t$时刻某只蚂蚁可能爬到了$x$号水滴的位置。
用set从左往右记录所有落下且未消失的水滴,那么:
对于事件(1):将$x$插入set后,找到前驱和后继,更新区间内的$v$。然后在线段树上二分找到往左往右最近的蚂蚁,将新的事件(2)放入堆中。
对于事件(2):首先检查对应位置是否真的有蚂蚁,如果真的有,且$x$号水滴未消失,那么找到前驱和后继,更新区间内的$v$,并找到往左往右最近的蚂蚁,将新的事件(2)放入堆中,并删除$x$。
每次发生新的事件时,需要将所有蚂蚁的$f$都加上$v\times$时间差,同样可以用线段树打标记维护。
时间复杂度$O(m\log n)$。
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
#include<set>
using namespace std;
typedef long long ll;
typedef pair<ll,int>P;
const int N=250005,M=524305;
const ll inf=1LL<<50;
int n,m,i,x,ant[N],water[N],cnt;
bool del[N];
ll last;
set<P>T;
priority_queue<P,vector<P>,greater<P> >q;
ll fl[M],fr[M];int vl[M],vr[M];
ll ta[M],tb[M];int tc[M],td[M];
inline void tag1(int x,ll a,ll b,int c,int d){
ta[x]+=tc[x]*a;
tb[x]+=td[x]*a+b;
tc[x]*=c;
td[x]=td[x]*c+d;
fl[x]+=vl[x]*a+b;
vl[x]=vl[x]*c+d;
fr[x]+=vr[x]*a+b;
vr[x]=vr[x]*c+d;
}
inline void pb(int x){
if(ta[x]||tb[x]||tc[x]!=1||td[x]){
tag1(x<<1,ta[x],tb[x],tc[x],td[x]);
tag1(x<<1|1,ta[x],tb[x],tc[x],td[x]);
ta[x]=tb[x]=td[x]=0,tc[x]=1;
}
}
void build(int x,int a,int b){
tc[x]=1;
fl[x]=ant[a];
fr[x]=ant[b];
if(a==b)return;
int mid=(a+b)>>1;
build(x<<1,a,mid);
build(x<<1|1,mid+1,b);
}
void change(int x,int a,int b,ll c,ll d,int p){
if(c>d)return;
if(c>fr[x]||d<fl[x])return;
if(c<=fl[x]&&fr[x]<=d){tag1(x,0,0,0,p);return;}
if(a==b)return;
pb(x);
int mid=(a+b)>>1;
change(x<<1,a,mid,c,d,p);
change(x<<1|1,mid+1,b,c,d,p);
fl[x]=fl[x<<1];
fr[x]=fr[x<<1|1];
vl[x]=vl[x<<1];
vr[x]=vr[x<<1|1];
}
ll askr(int x,int a,int b,ll p){
if(p<fl[x])return -inf;
if(p>=fr[x])return fr[x];
if(a==b)return -inf;
pb(x);
int mid=(a+b)>>1;
return max(askr(x<<1,a,mid,p),askr(x<<1|1,mid+1,b,p));
}
ll askl(int x,int a,int b,ll p){
if(p>fr[x])return inf;
if(p<=fl[x])return fl[x];
if(a==b)return inf;
pb(x);
int mid=(a+b)>>1;
return min(askl(x<<1,a,mid,p),askl(x<<1|1,mid+1,b,p));
}
void dfs(int x,int a,int b){
if(a==b){printf("%lld ",fl[x]);return;}
int mid=(a+b)>>1;
pb(x);
dfs(x<<1,a,mid);
dfs(x<<1|1,mid+1,b);
}
inline ll cal(ll a,ll b){return(a+b)/2;}
int main(){
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&ant[i]);
build(1,1,n);
scanf("%d",&m);
for(i=1;i<=m;i++)scanf("%d%d",&x,&water[i]),q.push(P(x,-i));
T.insert(P(-inf,0));
T.insert(P(inf,0));
while(!q.empty()){
P t=q.top();q.pop();
tag1(1,t.first-last,0,1,0);
last=t.first;
x=t.second;
if(x<0){
x=-x;
P now(water[x],x);
T.insert(now);
set<P>::iterator it=T.find(now),pre=it,nxt=it;
pre--,nxt++;
ll A=pre->first,B=it->first,C=nxt->first;
ll l=askr(1,1,n,B),r=askl(1,1,n,B);
if(l>-inf)q.push(P(B-l+last,x));
if(r<inf)q.push(P(r-B+last,x));
change(1,1,n,A+1,min(cal(A,B),B-1),-1);
change(1,1,n,max(A+1,cal(A,B)+1),B-1,1);
change(1,1,n,B,B,0);
change(1,1,n,B+1,min(cal(B,C),C-1),-1);
change(1,1,n,max(B+1,cal(B,C)+1),C-1,1);
}else{
if(del[x]||askr(1,1,n,water[x])!=water[x])continue;
del[x]=1;
cnt++;
if(cnt==m)break;
P now(water[x],x);
set<P>::iterator it=T.find(now),pre=it,nxt=it;
pre--,nxt++;
ll A=pre->first,B=nxt->first;
T.erase(now);
if(!pre->second&&!nxt->second){
tag1(1,0,0,0,0);
}else{
if(pre->second){
ll r=askl(1,1,n,A);
if(r<inf)q.push(P(r-A+last,pre->second));
}
if(nxt->second){
ll l=askr(1,1,n,B);
if(l>-inf)q.push(P(B-l+last,nxt->second));
}
change(1,1,n,A+1,min(cal(A,B),B-1),-1);
change(1,1,n,max(A+1,cal(A,B)+1),B-1,1);
}
}
}
dfs(1,1,n);
}
Trial Finals:
Loteria 2
首先特判$k=2$的情况,此时只有两种方案。
当$k\geq 3$时,问题等价于保留最多位不去修改。容易发现保留的位置需要满足相邻两个位置间隔至少为$1$或者字符不同。
设$f[i]$表示考虑了前$i$个字符且$a[i]$保留时,最多能保留多少位,则$f[i]=\max(f[i-1][a[i]\neq a[i-1]],f[j](j<i-1),0)+1$。
时间复杂度$O(n)$。
#include<cstdio>
const int N=500010;
int n,k,i,a[N],f[N],g[N],A,B;
inline void up(int&a,int b){a<b?(a=b):0;}
int main(){
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)scanf("%d",&a[i]);
if(k==2){
for(i=1;i<=n;i++){
if((i&1)&&a[i]!=1)A++;
if((i&1)&&a[i]!=2)B++;
if(!(i&1)&&a[i]!=2)A++;
if(!(i&1)&&a[i]!=1)B++;
}
return printf("%d",A<B?A:B),0;
}
for(i=1;i<=n;i++){
f[i]=0;
if(a[i]!=a[i-1])f[i]=f[i-1];
if(i>1)up(f[i],g[i-2]);
g[i]=g[i-1];
up(g[i],++f[i]);
}
printf("%d",n-g[n]);
}
Finals:
Bajtokrąg
求出$d_x$表示首都到$x$点的最短路,如果直径有一个端点是首都,则答案为$\max(d_x)$,下面考虑直径端点不是首都的情况。
令$len$为外围总环长,$s_x$为$1$顺时针到$x$的路径长度,则
$dis(i,j)=\min(d_i+d_j,s_j-s_i,len-s_j+s_i)$,其中$i<j$。
将环倍长,破环成链。
枚举$i$,则需要找到$j$ $(i<j\leq i+n-2)$满足$\min(d_i+d_j,s_j-s_i,len-s_j+s_i)$最大。
第一种情况:$s_j-s_i\leq len-s_j+s_i$,则$i<j\leq lim$。
- 若$d_i+d_j\leq s_j-s_i$,则需要查询$d_j-s_j\leq -d_i-s_i$的$j$里$d_j$的最大值。
- 若$d_i+d_j\geq s_j-s_i$,则需要查询$d_j-s_j\geq -d_i-s_i$的$j$里$s_j$的最大值。
第二种情况:$s_j-s_i\geq len-s_j+s_i$,则$lim<j\leq i+n-2$。
- 若$d_i+d_j\leq len-s_j+s_i$,则需要查询$d_j+s_j\leq len-d_i+s_i$的$j$里$d_j$的最大值。
- 若$d_i+d_j\geq len-s_j+s_i$,则需要查询$d_j+s_j\geq len-d_i+s_i$的$j$里$-s_j$的最大值。
双指针$lim$的同时用线段树维护区间最值即可。
时间复杂度$O(n\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=500005,M=1111111;
const ll inf=1LL<<60;
int n,i,j,a[N];ll d[N],s[N],_w[N],sum,ans;
inline void umax(ll&a,ll b){a<b?(a=b):0;}
inline void umin(ll&a,ll b){a>b?(a=b):0;}
inline bool cmp(int x,int y){return _w[x]<_w[y];}
struct DS{
int q[N],at[N],pos[N];ll w[N],f[M],g[M];
void ext(int x,ll y){w[x]=y;}
void build(int x,int a,int b){
f[x]=g[x]=-inf;
if(a==b){
pos[a]=x;
return;
}
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
}
inline void change(int x,ll A,ll B){
x=pos[at[x]];
f[x]=A,g[x]=B;
for(x>>=1;x;x>>=1)f[x]=max(f[x<<1],f[x<<1|1]),g[x]=max(g[x<<1],g[x<<1|1]);
}
inline ll askf(ll p){
ll ret=-inf;
int x=1,a=1,b=n,mid;
while(1){
if(w[b]<=p){
umax(ret,f[x]);
break;
}
if(w[a]>p)break;
mid=(a+b)>>1;
if(w[mid]<=p){
umax(ret,f[x<<1]);
x=x<<1|1;
a=mid+1;
}else{
x<<=1;
b=mid;
}
}
return ret;
}
inline ll askg(ll p){
ll ret=-inf;
int x=1,a=1,b=n,mid;
while(1){
if(w[a]>=p){
umax(ret,g[x]);
break;
}
if(w[b]<p)break;
mid=(a+b)>>1;
if(w[mid+1]>=p){
umax(ret,g[x<<1|1]);
x<<=1;
b=mid;
}else{
x=x<<1|1;
a=mid+1;
}
}
return ret;
}
void init(){
for(i=1;i<=n;i++)q[i]=i,_w[i]=w[i];
sort(q+1,q+n+1,cmp);
for(i=1;i<=n;i++)at[q[i]]=i,w[i]=_w[q[i]];
build(1,1,n);
}
}A,B;
int main(){
scanf("%d",&n);n--;
for(i=1;i<=n;i++)scanf("%d",&a[i]),s[i+1]=s[i]+a[i];
sum=s[n+1];
for(i=1;i<=n;i++)scanf("%lld",&d[i]);
for(j=0;j<2;j++){
for(i=1;i<n;i++)umin(d[i+1],d[i]+a[i]);
umin(d[1],d[n]+a[n]);
}
for(j=0;j<2;j++){
for(i=n-1;i;i--)umin(d[i],d[i+1]+a[i]);
umin(d[n],d[1]+a[n]);
}
for(i=1;i<=n;i++)umax(ans,d[i]);
for(i=1;i<=n;i++)A.ext(i,d[i]-s[i]),B.ext(i,d[i]+s[i]);
A.init(),B.init();
for(i=j=2;i<=n;i++)B.change(i,d[i],-s[i]);
for(i=1;i<=n;i++){
A.change(i,-inf,-inf),B.change(i,-inf,-inf);
if(j<i+1)j=i+1;
while(j<=n&&s[j]-s[i]<sum-s[j]+s[i]){
A.change(j,d[j],s[j]);
B.change(j,-inf,-inf);
j++;
}
umax(ans,A.askf(-d[i]-s[i])+d[i]);
umax(ans,A.askg(-d[i]-s[i])-s[i]);
umax(ans,B.askf(sum-d[i]+s[i])+d[i]);
umax(ans,B.askg(sum-d[i]+s[i])+s[i]+sum);
}
printf("%lld",ans);
}
Euler's Problem
首先枚举$n$的每个约数$d$,检查一下$d+1$是否是质数,这些数都有可能作为答案的质因子出现。
考虑爆搜,每次枚举下一个要在答案中出现的质因子$p$,将$n$除以$p-1$,再枚举$p$的指数,然后递归搜索。
需要加一些剪枝:
$1.$当$n=1$的时候说明找到了一组合法解,直接返回。
$2.$只有当$p-1|n$时才有可能有解,因此设$g[i][j]$表示第$i$个约数在第$j$个质数之后第一个能被整除的位置。
那么可以沿着$g$进行枚举,每次枚举到的必然是$n$的约数。
$3.$对于如何判断一个$d$是$n$的第几个约数,可以用两个数组进行重标号:
$small[d]$表示$d(d\leq\sqrt{n})$是$n$的第几个约数。
$big[d]$表示$\frac{n}{d}(\frac{n}{d}>\sqrt{n})$是$n$的第几个约数。
#include<cstdio>
#include<algorithm>
typedef long long ll;
const int N=1000000,M=5000;
int T,lim,m,d,cnt,i,j,p[N/10],tot,small[N],big[N],g[M][700];bool v[N];ll n,a[M],b[M],q[N];
inline bool check(ll n){
if(n<N)return !v[n];
for(int i=2;1LL*i*i<=n;i++)if(n%i==0)return 0;
return 1;
}
void dfs(int x,ll S,ll p){
if(p==1){q[cnt++]=S;return;}
x=g[p<=lim?small[p]:big[n/p]][x];
if(x==m)return;
dfs(x+1,S,p);
for(dfs(x+1,S*=a[x],p/=a[x]-1);p%a[x]==0;dfs(x+1,S*=a[x],p/=a[x]));
}
int main(){
for(i=2;i<N;i++){
if(!v[i])p[tot++]=i;
for(j=0;j<tot&&i*p[j]<N;j++){
v[i*p[j]]=1;
if(i%p[j]==0)break;
}
}
scanf("%d",&T);
while(T--){
scanf("%lld",&n);
if(n==1){puts("2\n1 2");continue;}
for(lim=1;1LL*(lim+1)*(lim+1)<=n;lim++);
for(cnt=m=d=0,i=1;i<=lim;i++)if(n%i==0){
if(check(i+1))a[m++]=i+1;
b[d++]=i;
if(1LL*i*i!=n){
if(check(n/i+1))a[m++]=n/i+1;
b[d++]=n/i;
}
}
std::sort(a,a+m),std::sort(b,b+d);
for(i=0;i<d;i++){
if(b[i]<=lim)small[b[i]]=i;else big[n/b[i]]=i;
for(g[i][m]=m,j=m-1;~j;j--)g[i][j]=b[i]%(a[j]-1)?g[i][j+1]:j;
}
dfs(0,1,n);
std::sort(q,q+cnt);
printf("%d\n",cnt);
if(cnt)for(printf("%lld",q[0]),i=1;i<cnt;i++)printf(" %lld",q[i]);
puts("");
}
return 0;
}
Stone Game
如果$n$是奇数,那么先手必败;如果$n$是偶数,那么第一步一定要拿$\frac{n}{2}$,于是可以交换先后手递归到$\frac{n}{2}$的子问题。
时间复杂度$O(\log n)$。
#include<cstdio>
int Case,n;
bool dfs(int n){
if(n&1)return 0;
return !dfs(n>>1);
}
int main(){
scanf("%d",&Case);
while(Case--)scanf("%d",&n),puts(dfs(n)?"TAK":"NIE");
}
Planar Graph
留坑。
Blizzard
首先离散化,即相邻关键点之间的部分可以压成一段。
注意到区间互不包含,因此排序后每个位置的清理影响到的是一段连续区间的清理工的工作长度。
这显然可以用线段树维护,支持区间减去一个数,单点加上$+\infty$,以及查询全局最小值。
对于每次清理,暴力枚举区间内所有没清理过的段,在线段树中区间修改,用并查集进行路径压缩即可。
时间复杂度$O(n\log n)$。
#include<cstdio>
#include<algorithm>
using namespace std;
typedef pair<int,int>P;
const int N=300010,M=1050000,inf=1000000010;
int n,m,i,j,x,b[N<<1],f[N<<1],tag[M];P v[M];struct E{int l,r;}a[N];
inline void read(int&a){char c;while(!(((c=getchar())>='0')&&(c<='9')));a=c-'0';while(((c=getchar())>='0')&&(c<='9'))(a*=10)+=c-'0';}
inline void add(int x,int p){v[x].first+=p;tag[x]+=p;}
inline void pb(int x){if(tag[x])add(x<<1,tag[x]),add(x<<1|1,tag[x]),tag[x]=0;}
void build(int x,int a,int b){
if(a==b){v[x]=P(::a[a].r-::a[a].l,a);return;}
int mid=(a+b)>>1;
build(x<<1,a,mid),build(x<<1|1,mid+1,b);
v[x]=min(v[x<<1],v[x<<1|1]);
}
void del(int x,int a,int b,int c){
if(a==b){v[x].first+=inf;return;}
pb(x);
int mid=(a+b)>>1;
if(c<=mid)del(x<<1,a,mid,c);else del(x<<1|1,mid+1,b,c);
v[x]=min(v[x<<1],v[x<<1|1]);
}
void change(int x,int a,int b,int c,int d,int p){
if(c<=a&&b<=d){add(x,p);return;}
pb(x);
int mid=(a+b)>>1;
if(c<=mid)change(x<<1,a,mid,c,d,p);
if(d>mid)change(x<<1|1,mid+1,b,c,d,p);
v[x]=min(v[x<<1],v[x<<1|1]);
}
int F(int x){return f[x]==x?x:f[x]=F(f[x]);}
inline int lower(int x){
int l=1,r=m,mid,t;
while(l<=r)if(b[mid=(l+r)>>1]<=x)l=(t=mid)+1;else r=mid-1;
return t;
}
inline int getl(int c,int d){
int l=1,r=n,mid,t;
while(l<=r){
mid=(l+r)>>1;
if(a[mid].r<=c)l=mid+1;
else if(a[mid].l>=d)r=mid-1;
else r=(t=mid)-1;
}
return t;
}
inline int getr(int c,int d){
int l=1,r=n,mid,t;
while(l<=r){
mid=(l+r)>>1;
if(a[mid].r<=c)l=mid+1;
else if(a[mid].l>=d)r=mid-1;
else l=(t=mid)+1;
}
return t;
}
inline void clean(int l,int r){
int x=lower(l);
while(1){
x=F(x);
if(b[x]>=r)return;
f[x]++;
change(1,1,n,getl(b[x],b[x+1]),getr(b[x],b[x+1]),b[x]-b[x+1]);
}
}
int main(){
read(n);read(n);
for(i=1;i<=n;i++){
read(a[i].l),read(a[i].r);
b[++m]=a[i].l,b[++m]=a[i].r;
}
sort(b+1,b+m+1);
for(i=1;i<=m;i++)if(b[i]!=b[i-1])b[++j]=b[i];
m=j;
for(i=1;i<=m;i++)f[i]=i;
build(1,1,n);
for(i=1;i<=n;i++){
x=v[1].second;
printf("%d\n",x);
del(1,1,n,x);
clean(a[x].l,a[x].r);
}
return 0;
}
Glowworms
给定时刻后答案等于两维坐标极差的最大值,注意到两个极差都是凸函数,取$\max$也是,所以三分找到最小值即可。
时间复杂度$O(n\log ans)$。
#include<cstdio>
typedef double ld;
const int N=100010;
const ld inf=1e100;
int n,i,_,x[N],y[N],a[N],b[N];ld l,r,len,m1,m2,f1,f2,ans;
inline void umin(ld&a,ld b){a>b?(a=b):0;}
inline void umax(ld&a,ld b){a<b?(a=b):0;}
ld cal(ld t){
ld xl=inf,xr=-inf,yl=inf,yr=-inf,tmp;
for(int i=1;i<=n;i++){
tmp=x[i]+a[i]*t;
umin(xl,tmp),umax(xr,tmp);
tmp=y[i]+b[i]*t;
umin(yl,tmp),umax(yr,tmp);
}
xr-=xl,yr-=yl;
umax(xr,yr);
return xr;
}
int main(){
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d%d%d%d",&x[i],&y[i],&a[i],&b[i]);
l=0,r=1e9,ans=1e7;
for(_=100;_--;){
len=(r-l)/3;
umin(ans,f1=cal(m1=l+len));
umin(ans,f2=cal(m2=r-len));
if(f1<f2)r=m2;else l=m1;
}
printf("%.15f",ans);
}
Tester wioseł
对于信息$\max(a[i],a[j])\geq y[i][j]$,我们可以得到命题$a[i]\geq y[i][j]$和命题$a[j]\geq y[i][j]$至少有一个为真,在这里我们得到了$O(n^2)$个命题和$O(n^2)$个二元关系。
对于信息$a[i]+a[j]\leq x[i][j]$,我们枚举和$a[i]$以及$a[j]$有关的所有$O(n^2)$个命题对,如果一对命题的$y$值之和$>x[i][j]$,则这两个命题不能同时为真。
因此我们得到了一个2-SAT问题,直接建图将会得到$O(n^2)$个点和$O(n^4)$条边,边数不能接受。
考虑使用Kosaraju算法求2-SAT问题对应图的SCC的过程,我们需要DFS到所有点,已经访问过的点不需要重复DFS。
因此对于一个命题$a[i]\geq y[i][j]$,它代表的点$p$要与所有冲突的命题代表的点连边。
当我们DFS到$p$点时,枚举另一个命题代表的变量$a[k]$,则要连边的点是所有形如$a[k]\geq y'$的命题,其中$y[i][j]+y'>x[i][k]$,即$y'>x[i][k]-y[i][j]$。
对于每个变量$a[k]$,将所有涉及它的命题按$y$从小到大排序,则$p$点要继续DFS的点是一段后缀,记录最靠后的未访问过的点即可,每个命题总计只会被遍历到$O(1)$次。
时间复杂度$O(n^3)$。
#pragma GCC optimize("-Ofast","-funroll-all-loops","-ffast-math")
#pragma GCC optimize("-fno-math-errno")
#pragma GCC optimize("-funsafe-math-optimizations")
#pragma GCC optimize("-freciprocal-math")
#pragma GCC optimize("-fno-trapping-math")
#pragma GCC optimize("-ffinite-math-only")
#pragma GCC optimize("-fno-stack-protector")
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=305,M=N*N,BUF=3000005;
char Buf[BUF],*buf=Buf;
int n,L,R,tot,i,j,x,y,a[N],f[N][N],g[N][N],who[M],val[M];
int p[M],pool[N][N],cp[N];
bool vis[M];int q[M],t,at[M],cnt;
inline void read(int&a){for(a=0;*buf<48;buf++);while(*buf>47)a=a*10+*buf++-48;}
inline bool cmp(int x,int y){return val[x]<val[y];}
inline void umin(int&a,int b){a>b?(a=b):0;}
inline void umax(int&a,int b){a<b?(a=b):0;}
/*
val[x]+val[y]>f[who[x]][who[y]]
x->y^1
y->x^1
val[x^1]+val[y]>f[who[x^1]][who[y]]
y->x
*/
void dfs0(int x){
if(vis[x])return;
vis[x]=1;
//for all y such that val[x]+val[y]>f[who[x]][who[y]], dfs y^1
int A=who[x],B=val[x];
while(L<=R&&!cp[L])L++;
while(L<=R&&!cp[R])R--;
for(int i=L;i<=R;i++)if(cp[i]){
int lim=f[A][i]-B,&j=cp[i];
while(j){
int k=pool[i][j];
if(val[k]<=lim)break;
j--;
dfs0(k^1);
}
}
q[++t]=x;
}
void dfs1(int x){
if(!vis[x])return;
vis[x]=0,at[x]=cnt;
//for all y such that val[x^1]+val[y]>f[who[x^1]][who[y]], dfs y
int A=who[x^1],B=val[x^1];
while(L<=R&&!cp[L])L++;
while(L<=R&&!cp[R])R--;
for(int i=L;i<=R;i++)if(cp[i]){
int lim=f[A][i]-B,&j=cp[i];
while(j){
int k=pool[i][j];
if(val[k]<=lim)break;
j--;
dfs1(k);
}
}
}
int main(){
fread(Buf,1,BUF,stdin);read(n);
for(i=1;i<=n;i++)for(j=1;j<=n;j++)read(f[i][j]);
for(i=1;i<=n;i++)for(j=1;j<=n;j++)read(g[i][j]);
for(i=1;i<=n;i++)for(j=1;j<=i;j++){
umin(f[i][j],f[j][i]);
umin(f[j][i],f[i][j]);
umax(g[i][j],g[j][i]);
who[tot<<1]=i;
who[tot<<1|1]=j;
val[tot<<1]=val[tot<<1|1]=g[i][j];
tot++;
}
for(i=0;i<tot*2;i++)p[i]=i;
sort(p,p+tot*2,cmp);
for(i=0;i<tot*2;i++){
x=p[i];
y=who[x];
pool[y][++cp[y]]=x;
}
L=1,R=n;
for(i=0;i<tot*2;i++)if(!vis[i])dfs0(i);
for(i=1;i<=n;i++)cp[i]=0;
for(i=0;i<tot*2;i++){
x=p[i];
y=who[x];
pool[y][++cp[y]]=x;
}
L=1,R=n;
for(i=t;i;i--)if(vis[q[i]])cnt++,dfs1(q[i]);
for(i=0;i<tot*2;i++)if(at[i]>at[i^1])umax(a[who[i]],val[i]);
for(i=1;i<=n;i++)printf("%d%c",a[i],i<n?' ':'\n');
}