| 这个作业属于哪个班级 | 数据结构 |
|---|---|
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 | 学习图结构设计及运算操作 |
| 姓名 | 曹卉潼 |
0.PTA得分截图

1.本周学习总结(6分)

1.1 图的存储结构
1.1.1 邻接矩阵(不用PPT上的图)
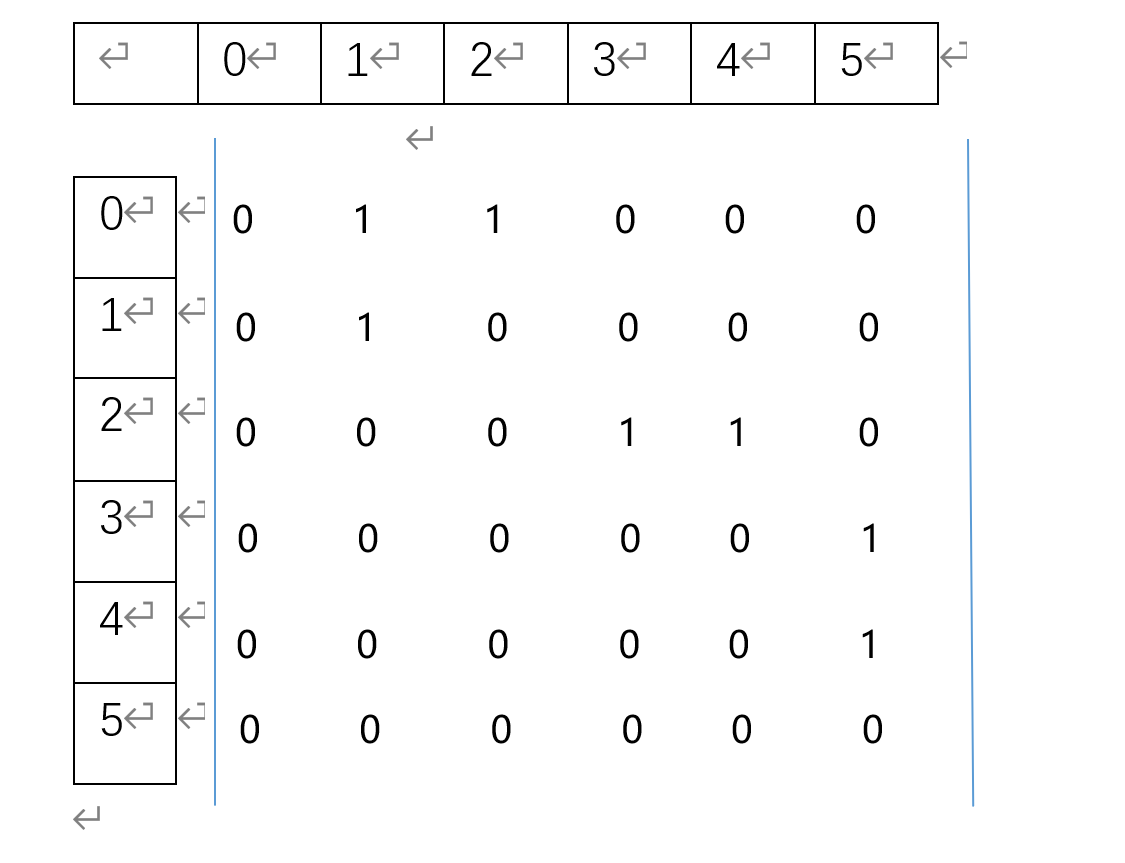
造一个图,展示其对应邻接矩阵
用一个二维数组edges[][]保存两个顶点之间的关系。edges[i][j]表示从第i个顶点到第j个顶点的边信息。我们可以根据该二维数组每一行的数据判断每个顶点的入度,根据每一列的数据判断每个顶点的出度。每个顶点的其他信息(例如:顶点名称,顶点编号等)用一个一维数组去vexs[]保存;
结构体定义
typedef struct
{
int **edges;//保存边关系,定义为二级指针的原因:可以根据结点个数申请相对的空间,提高空间的利用效率;
int n,e;//n保存顶点个数,e保存图中边的条数;
VertexType *vexs;//保存顶点其他信息;VertexType是顶点其他信息的类型,可以是int,char,或者自定义结构体等;
}
无向图
对于无向图来说,两个顶点之间存在一条边(i,j),那么这两个顶点互为邻接点,不仅可以从顶点i到顶点j,也可以从顶点j到顶点i。于是在建立邻接矩阵时,不仅要对edges[i][j]赋值,也要对edges[j][i]赋值(无权值,如果存在边就赋值为1,否则赋为0);于是我们可以看出,最后得到无向图的邻接矩阵一定是沿对角线对称的


有向图
对于有向图来说,若存在一条边(i,j),则此边只表示为从顶点i到顶点j,不可以由边(i,j)得到可以从顶点j到顶点i的信息。所以在建有向图的邻接矩阵时,只对edges[i][j]赋值(无权值,如果存在边就赋值为1,否则赋为0);和无向图不一样的是,最后得到的邻接矩阵不一定是一个对称图形。

创建领接矩阵函数

1.1.2 邻接表
造一个图,展示其对应邻接表(不用PPT上的图)
邻接表是数组和链表的结合。对于每个顶点都建立一个单链表存储该顶点所有的邻接点。然后将定义一个结构体VNode,里面保存顶点邻接点的链表和顶点其他信息。设置VNode类型的结构体数组AdjGraph[]就可以保存图中所有顶点的邻接点,达到保存图中所有边的目的。结构体数组AdjGraph[]即为邻接表。
邻接表的结构体定义
typedef struct ANode //边结点;
{
int adjvex;//指向该边的终点编号;
struct ANode*nextarc;//指向下一个邻接点;
INfoType info;//保存该边的权值等信息;
}ArcNode;
typedef struct //头结点
{
int data;//顶点;
ArcNode *firstarc;//指向第一个邻接点;
}VNode;
typedef struct
{
VNode adjlist[MAX];//邻接表;
int n,e;//图中顶点数n和边数e;
}AdjGraph;
无向图
对于无向图,输入边(a,b),那么就代表可以从顶点a到顶点b,也可以从顶点b到顶点a,所以我们不仅要在顶点a的邻接点链表中插入结点b,还要在顶点b的邻接点链表中插入结点a。


有向图
对于有向图,输入边(a,b),只需在顶点a的邻接点链表中插入b就行。


创建邻接表函数

1.1.3 邻接矩阵和邻接表表示图的区别
(1)邻接矩阵:
- 因为邻接矩阵需要申请一个二维数组,空间复杂度为O(n2),邻接矩阵的初始化需要初始化整个二维数组,所以时间复杂度为O(n2);
- 好处:方便我们提取,修改边的信息;
- 劣势:占用空间较大,如果图中边条数较少(稀疏图)的话,需要我们保存的边信息就比较少,用邻接矩阵就会有多余的空间被闲置,空间利用效率不高;不利于顶点的插入和删除。
(2)邻接表:
- 因为共有e条边和n个结点,需要开辟n个空间来保存结点,e个空间来保存e条边信息,所以,创建邻接表的空间复杂度为O(n+e);因为对n个结点的单链表进行初始化,处理了n次,还要对e条边信息进行保存,故时间复杂度为O(n+e);
- 优势:占用空间相对邻接矩阵来说较小。
- 劣势:不方便我们提取两个顶点之间边的信息。
1.2 图遍历
1.2.1 深度优先遍历
DFS遍历
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。

深度遍历代码

深度遍历适用哪些问题的求解。(可百度搜索)
1.2.2 广度优先遍历
选上述的图,继续介绍广度优先遍历结果
BFS遍历
从给定的任意结点v(初始顶点)开始,访问v所有的未被访问过的邻接点,然后按照一定次序访问每一个顶点的所有未被访问过的邻接点,直到图中和初始顶点邻接的所有顶点都被访问过为止。BFS遍历我们在用队列求解迷宫问题时接触过,是不可回溯的,逐渐向外扩散的过程。

建一个访问队列q;
访问v节点,进队;
while(队列不为空)
出队一个节点w;
遍历节点w的邻接点
取邻接点j,如果j未被访问则入队列q,然后把j标记为已访问;
end while
广度遍历代码

广度遍历适用哪些问题的求解。(可百度搜索)
1.3 最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。
对于带权值的图,其中权值之和最小的生成树称为图的最小生成树。
1.3.1 Prim算法求最小生成树
基于上述图结构求Prim算法生成的最小生成树的边序列
实现Prim算法的2个辅助数组是什么?其作用是什么?
设置2个辅助数组:
1.closest[i]:最小生成树的边依附在U中顶点编号。
2.lowcost[i]表示顶点i(i ∈ V-U)到U中顶点的边权重,取最小权重的顶点k加入U。
并规定lowcost[k]=0表示这个顶点在U中
每次选出顶点k后,要队lowcost[]和closest[]数组进行修正
Prim算法代码
void Prim(MGraph g, int v)
{
int lowcost[MAXV], closest[MAXV];//lowcost表示到该点最短距离,closest
int i, j, k, min ;// k记录最近顶点的编号
lowcost[1] = 1;//起点最近点为它本身
for (i = 1; i <= g.n; i++) //顶点从1开始,给lowcost[]和closest[]置初值
{
lowcost[i] = g.edges[v][i];//建图时未有直接相连的边,lowcost=edges为无穷大INF
closest[i] = v;
}
for (i = 1; i < g.n; i++) //找(n-1)次剩下的顶点
{
min = INF;
for (j = 1; j <= g.n; j++) // 在(V-U)中找出离U最近的顶点k
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j]; k = j; //
}
lowcost[k] = 0; //遍历所有点后找到距离最近点,标记k已经加入
for (j = 1; j <= g.n; j++) //修改数组lowcost和closest
if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
{
lowcost[j] = g.edges[k][j];
closest[j] = k;
}
}
}
分析Prim算法时间复杂度
Prim()算法中有两重for循环,时间复杂度为O(n^2),n为图的顶点个数。其执行时间与图中边数e无关,所以适合用稠密图求最小生成树。
1.3.2 Kruskal算法求解最小生成树
克鲁斯卡尔算法过程:
(1)置U的初值等于V(即包含有G中的全部顶点),TE(最小生成树的边集)的初值为空集(即图T中每一个顶点都构成一个连通分量)。
(2)将图G中的边按权值从小到大的顺序依次选取:
若选取的边未使生成树T形成回路,则加入TE;
否则舍弃,直到TE中包含(n-1)条边为止。
实现Kruskal算法的辅助数据结构
由于克鲁斯卡尔算法过程是对边的权重排序选边,因此我们需要另外一个存储结构来存储边的权重信息
typedef struct
{ int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
} Edge;
Edge E[MAXV];
Kruskal算法代码


分析Kruskal算法时间复杂度
连通图G有n个顶点、e条边,其时间复杂度为O(e^2)。该算法的执行时间只与图的边数有关,与顶点数无关,适用于稀疏图求最小生成树。
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
基于上述图结构,求解某个顶点到其他顶点最短路径。(结合dist数组、path数组求解)
最短路径与最小生成树不同:
最小生成树需要包含所有顶点, 而最短路径只考虑路径最短
1.从T中选取一个其距离值为最小的顶点W, 加入S
2.S中加入顶点w后,对T中顶点的距离值进行修改:
若加进W作中间顶点,从V0到Vj的距离值比不加W的路径要短,则修改此距离值;
3.重复上述步骤1,直到S中包含所有顶点,即S=V为止。
Dijkstra算法代码
void Dijkstra(MGraph g, int v)//源点v到其他顶点最短路径
{
int dist[MAXV], path[MAXV],s[MAXV];
int mindistance,u;//u为每次所选最短路径点
for (int i = 0; i < g.n; i++)//初始化各数组
{
s[i] = 0;//初始已选入点置空
dist[i] = g.edges[v][i];//初始化最短路径
if (dist[i] < INF) path[i] = v;
else path[i] = -1;//即无直接到源点V的边,因此初始化为-1
}
s[v] = 1;//源点入表示已选
for (int j = 0; j < g.n; j++)//要将所有点都选入需循环n-1次
{
mindistance = INF;//每次选之前重置最短路径
for (int i = 1; i < g.n; i++)//每次都遍历源点以外其他点来选入点
{
if (s[i] == 0 && dist[i] < mindistance)//在未选的点中找到最短路径
{
mindistance = dist[i];
u = i;//u记录选入点
}
}
s[u] = 1;//最后记录的u才为最后选入点
for (int i = 1; i < g.n; i++)//修正数组值
{
if (s[i] == 0)//!!仅需修改未被选入点的,已选入的既定
{
if (g.edges[u][i] < INF && dist[u] + g.edges[u][i] < dist[i])//先判断选入点到与该点存在时再比较判断
{
dist[i] = dist[u] + g.edges[u][i];
path[i] = u;
}
}
}
}
Dispath(dist, path, s, g.n, v);
}
Dijkstra算法的时间复杂度
1.时间复杂度为O(n^2)。
2.不适用带负权值的带权图求单源最短路径。
3. 不适用求最长路径长度:
最短路径长度是递增
顶点u加入S后,不会再修改源点v到u的最短路径长度
(按Dijkstra算法,找第一个距离源点S最远的点A,这个距离在以后就不会改变。但A与S的最远距离一般不是直连。)
1.4.2 Floyd算法求解最短路径
算法思路
有向图G=(V,E)采用邻接矩阵存储
二维数组A用于存放当前顶点之间的最短路径长度,分量A[i][j]表示当前顶点i到顶点j的最短路径长度。
递推产生一个矩阵序列A0,A1,…,Ak,…,An-1
Ak+1[i][j]表示从顶点i到顶点j的路径上所经过的顶点编号k+1的最短路径长度。
Floyd算法代码
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{
int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
{
A[i][j] = g.edges[i][j];
if (i != j && g.edges[i][j] < INF)
path[i][j] = i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j] = -1;
}
for (k = 0; k < g.n; k++) //求Ak[i][j]
{
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
if (A[i][j] > A[i][k] + A[k][j]) //找到更短路径
{
A[i][j] = A[i][k] + A[k][j]; //修改路径长度
path[i][j] = k; //修改经过顶点k
}
}
}
Floyd算法优势
1.弗洛伊德算法可以解决负权值的带权图,也可以解决求最长路径长度问题。
2.弗洛伊德算法是一种动态规划的算法,在规划的同时又对之前的内容进行调整修改。
1.5 拓扑排序
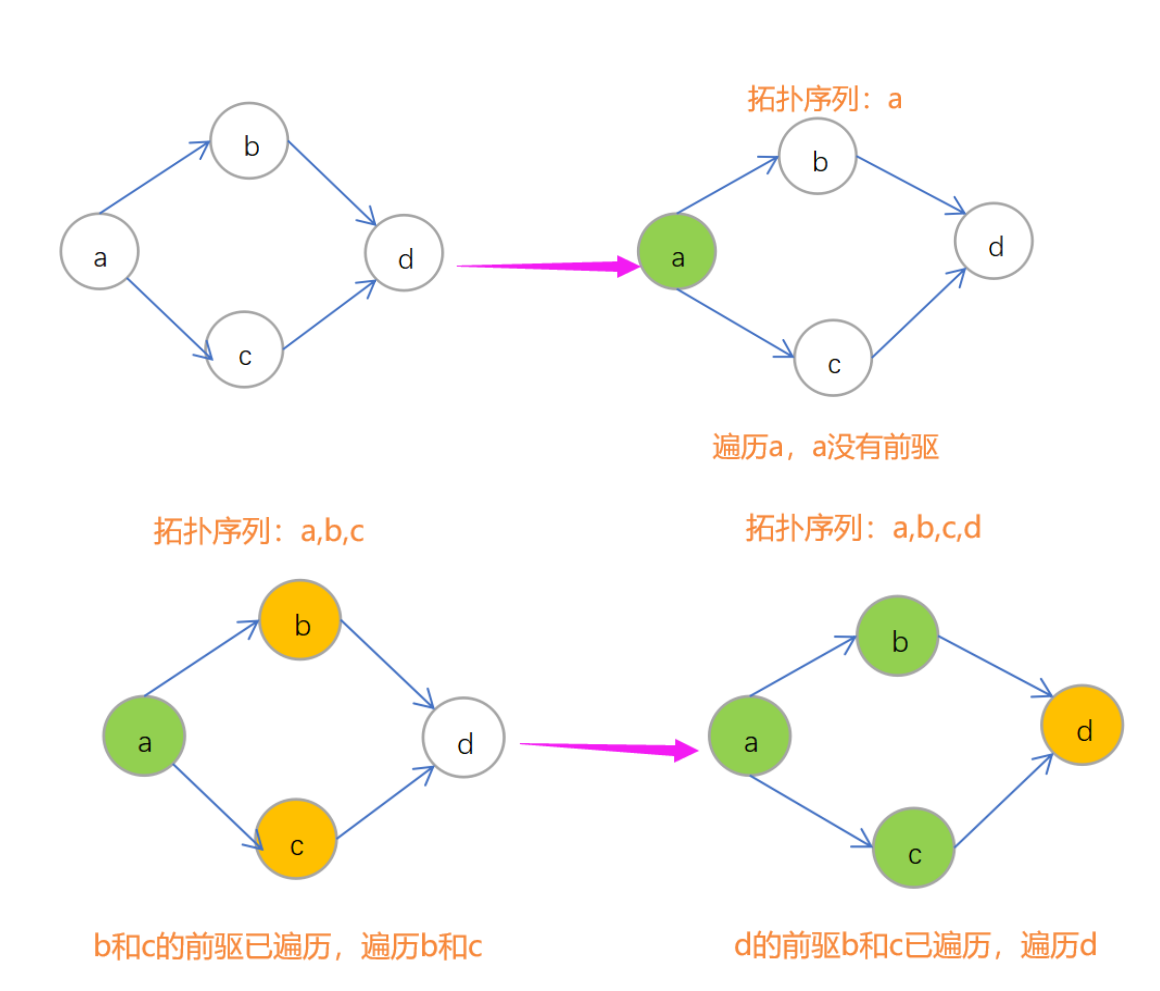
在一个有向图中,如果我们需要访问一个节点,要先把这个节点的所有前驱节点都访问过后,才能访问该节点。按照这样的顺序访问所有节点得到的序列叫做拓扑序列。在一个有向图中求一个拓扑序列的过程叫做拓扑排序。
拓扑排序思路
1.选择一个没有前驱结点的顶点,输出该顶点编号;
2.从有向图中删去此顶点,以及以他为起点的弧。这里的删除并不是在图结构中对该顶点的删除(物理删除),我们还是最好保留原来的图结构,这里我们可以借用顶点的入度实现模拟删除。当我们要'删除'某个顶点及以他为起点的弧时,我们可以直接将该顶点所有邻接点的入度-1;
重复上述两步,直到找不到没有前驱的顶点。
伪代码
遍历邻接表
计算每个顶点的入度,存入头结点count成员中;
遍历图顶点
找到一个入度为0的顶点,入栈/队列/数组;
while(栈不为空)
出栈结点v,访问;
遍历v的所有邻接点
{
所有邻接点的入度-1;
若有邻接点入度为0,入栈/队列/数组;
}
拓扑排序代码
void TopSort(AdjGraph* G)//邻接表拓扑排序
{
ArcNode* p;
int stack[MAXV], top=-1;//顺序栈结构
int visitedcout = 0;//记录已得到的拓扑序列长度
int sequence[MAXV];//用于保存拓扑序列
for (int i = 0; i < G->n; i++)
{
G->adjlist[i].count = 0;
}
for (int i = 0; i < G->n; i++)//遍历每条链,记录每个节点的入度
{
p = G->adjlist[i].firstarc;
while (p)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (int i = 0; i < G->n; i++)//先遍历图顶点,找出入度为0的点入栈
{
if (G->adjlist[i].count == 0)
{
top++; stack[top] = i;
}
}
int i = 0;
while (top!=-1)//接下来通过不断出栈过程中同时判断是否有点要入栈
{
sequence[i] = stack[top]; visitedcout++;//保存拓扑序列,并且记录已遍历点
p = G->adjlist[stack[top]].firstarc;//则该点的后继点入度都要减一
top--;//出栈
while (p)
{
G->adjlist[p->adjvex].count--;
if (G->adjlist[p->adjvex].count == 0)
{
top++; stack[top] = p->adjvex;
}
p = p->nextarc;
}
i++;
}
if (visitedcout == G->n)//则无环路得到拓扑序列,
{
cout << sequence[0];
for (int i = 1; i < G->n; i++)
{
cout << " " << sequence[i];
}
}
else cout << "error!";
}
用拓扑排序代码检查是否有环路

由上图可知,在一个环路中,我们是没办法找到入度为0的顶点。
同样的全局图来说,即使利用拓扑排序可以得到一定的拓扑序列,但只要存在环路,就不可能得到完整的拓扑序列
因此判断是否存在有环,只需记录一下得到的序列长度,与图的顶点数相比即可知,序列是否完整,是否就是拓扑序列
具体实现也已经在上述具体代码中体现
1.6 关键路径
什么叫AOE-网?
AOE-网(Activity ON Edge Network):
用顶点表示事件,用有向边e表示活动,边的权c(e)表示活动持续时间。是带权的有向无环图
整个工程完成的时间为:从有向图的源点到汇点的最长路径。又叫关键路径
求关键路径
1.对有向图拓扑排序
2.根据拓扑序列计算事件(顶点)的ve, vl数组
3.计算关键活动的e[],l[[]。即边的最早、最迟时间
4.找e=l边即为关键活动
5.关键活动连接起来就是关键路径
2.PTA实验作业(4分)
2.1 六度空间(2分)
2.1.1 伪代码
定义结点数n和边数e;
定义顶点访问标记数组visited[MAXV];
定义一个充当邻接矩阵的二维数组edgex[MAXV][MAXV];
int main()
输入n和e
for i=1 to e do
输入边的关系;
将edgex[][]对应的点的值改为1;
end for
for i=1 to n do
初始化visited数组 ;
调用BFS函数,返回距离不超过5的结点数;
计算并输出百分比;
end for
int BFS(int v)
定义一个队列qu;
将v入队;
visited[v]=1;
while 队不空且距离小于6 do
取队首做临时调用点temp;
循环遍历与该结点相连接的点
if 结点未遍历 then
结点数++;
入队;
visited[i]=1;
记录位置tail=i;
end if
if temp==last then
记录当前层数的最后一个元素的位置 ;
结点层数加一;
end if
end while
return count;
- 代码




2.1.2 提交列表

2.1.3 本题知识点
- 创建图函数运用了头插法
- 运用BFS遍历(引入队列)
- 不仅要用广度遍历BFS,还要和递归相结合,分层运算。
2.2 村村通
2.2.1 伪代码
main()函数
{
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
用二维数组代表邻接矩阵,并进行初始化。
}
for (i = 1; i <= e; i++)
{
给邻接矩阵赋值
}
调用普里姆算法;
}
Prim() 函数
{
for (i = 1; i <= n; i++)
{
给lowcost[]和closest[]置初值;
}
for (i = 1; i <n; i++)
{
给min赋初值(表示无穷);
for (j = 1; j <= n; j++)
{
在(V-U)中找出离U最近的顶点k
k记录最近顶点的编号
}
for (j = 1; j <= n; j++)
{
对(V-U)中的顶点j 进行调整;
修改数组lowcost[]和closest[];
}
}
输出num;
}
- 代码



2.2.2 提交列表

2.2.3 本题知识点
- main函数中运用二维数组代表邻接矩阵
- 运用Prim()算法