重读线性代数,一是为了重新理解Algebra的的重要概念以祭奠大一刷过的计算题,二是为了将来的学术工作先打下一点点(薄弱的)基础。数学毫无疑问是指导着的科研方向与科学发展,即使是同一本数学书,每次翻阅也能读出不同的内涵、享受不同的乐趣。
P1-149
Strang在书的序言便给出了linear algebra的研究对象,一切的来源便在于Ax=b这个方程组。虽然从向量矩阵、线性方程组到向量空间、线性变换,费了好大劲才将任意一个线性变化凝练到一个矩阵上,但对于Ax=b的经典案例的解空间的描述是连接矩阵、向量等数据元素和线性代数空间的不可或缺的纽带。这个思想被概括在了针对Ax=b的三个解法中:
1. forward elimination + backward substitution 其实就是中学的高斯消元法和代换法
2. b x inverse A,仅在矩阵A存在逆矩阵的时候可使用
3. Paticular + nullspace 构造解空间的方法,这里貌似道出了线性空间的真谛!如果仅有前两种方法,便没有space的概念了。
Vectors:何谓向量?一个对象的一组属性值?
空间中的向量本质上是群/环中的定义了运算的元素,它有很多运算性质(加法乘法内积外积),而最让我印象深刻的是它的相似性度量。向量天然带有可计算相似性的特征,包括两向量的距离、夹角等等,事实上在ML/DL/AI蓬勃发展的今天,许多工作也围绕这相似性度量而展开,尤其是我所学习的信息安全领域。今天阅读的一篇Dawn Song小组的文献提出了一种新的度量跨平台二进制代码相似性的办法就是摒弃了传统graph matching而改用embedding(一个数值向量)的,此类例子不胜枚举,即使是最简单的数学也能成为一个idea的动机。
Matrices:operation or features or weights
矩阵是最早的空间降维技术,在21世纪初研究人员研究随机搜索算法时,搜索的解空间数据形式的组织为向量,而Ax=b以及在A满秩情况下x与b的一一对应性质为向量的降维带来的最直接的手段。关于矩阵的四个操作:Elimination, Substitution, Factorization, Permutation. 前二者都是对方程组表征在空间上的矫正,第三个操作实际上给我带来了两个问题:一个矩阵到底有多少信息是有用的,是否存在冗余,高斯消元对信息量的影响是什么?一个普适的线性变换系统可以拆分为多个系统叠加,上三角/下三角阵系统是否隐含着一种时移性?对于我的这大部分疑惑作者都在解空间的章节中给出了答案。最后一个操作是行向量顺序的交换,在书中我暂时只看到体现出了计算上的差异。
Ax=b:
这个方程的左边:既可以看成是矩阵A对列向量x的线性变换,又可以看作是用列向量x的元素对矩阵A的列向量的线性组合。真巧,像是在宇宙中的某个空间内,线性变换等同于了线性组合。仔细想一想那只不过是矩阵的两个维度,原文对于A拆分成行或列是这么说的:three planes meet at a point & combines three columns to produce. 这里其实很具体只不过我没插图。
P150-199
Vector Space:
可以说是线性代数中最重要的概念了,我们平时讨论的问题、解空间大多都是R^n的子空间,满足8条性质构成了一个完美的度量环境(我一直在想它跟离散数学的群环域有什么联系,但貌似知识储备有点短缺...)。Dr. Strang在这里的分析真的是非常精妙,围绕Ax=b方程的解空间与矩阵A的特性,引出了关于矩阵A的四个空间(four foundational spaces):
1. Nullspace --- Ax=0的解空间,根据elimination操作将矩阵A化为梯形阵R之后,就可以得到pivot & free variables,pivot columns是线性无关的一组列向量(引出Rank和Basis),它构成了方程解的关键,free colums可以由之线性组合表示,这也说明了矩阵A的关键信息都包含在其中的一些列中而不一定是所有。针对free colum的特征很容易构造出special solution,再组合出所有解。Basis的概念在科研实际的应用也十分广泛,这周的paper reading会议上师姐分享的deblur in universal domain的方法就是把多个detector转化为一组基来使用,思想非常类似线性代数中空间的基向量,只不过原文作者用实验去寻找了向量个数的最优解,然鹅参照秩(rank)的概念我相信它是有理论最优的。
2. Column space --- 矩阵A列向量所有线性组合构成的向量空间,根据pivot / rank的概念,实际上也等价于其中部分关键列构成的列空间。
3. Row space --- 矩阵A行向量所有线性组合构成的向量空间,这一点几乎和column space平行,并且也可以利用pivot来简化(喵喵喵?突然好对称)
4. Left nullspace --- A^T的nullspace,这个概念就像是信号与系统里最后引入的FTFT,表面上它存在的最大的意义就是一块完整空间的拼图,让整个空间圆满起来。
整个叙述之中不乏有rank = dimension,A^-1之类的特殊例子讲解,最重要的是它的逻辑自洽让一个强迫症患者非常舒适。可是问题进一步又得到了更令人惊讶的一系列结论是:column space和row space向量一一对应,row space任意向量与null space所有向量垂直...于是正交便出现了。四个空间的关系:
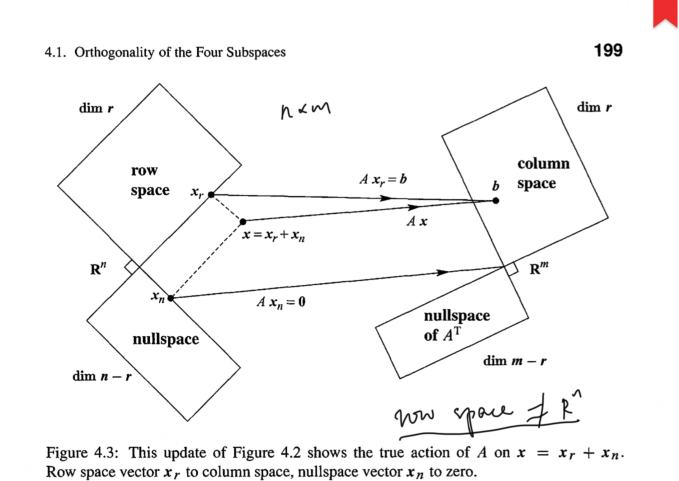
这里不上图没法表现出我的惊喜!而且作为这本书的封皮的图示,想必也是意义非凡。
总结一下:相比于你科编写的教材,这本经典的教科书更倾向于围绕着实际问题——线性方程组的解——来研究和讲解,而不是一条条的阐述经典概念,它让定义、理论、概念伴随着问题的研究而产生,恰如孔子云“吾道一以贯之”、“居其所而众星拱之”,它始终以经典问题为思考对象并自然地探索。我很享受这样的感觉,Prof. Weiping的以这种理念来教授的S&S课也是我这几年以来最享受的课程,那是我第一次考完试之后有一种”自己思考的浅薄对不起试卷的深度“的感觉。你科的有些教学内容什么什么的从2008年至9102也好多好多个年头了,与时俱进也是非常重要的叭。
大仲马在《基督山伯爵》书的结尾描述:人类的全部智慧就包含在了两个词中——等待与希望。套用这个公式,线性代数学的全部智慧就包含在一个方程中——Ax equals b. 最后,我想着反正我写的博客也没什么人看,虽然没写完我还是把它当作读书笔记挂出去了,这两周一边看一边改。