前言
学完了替罪羊树,我决定再去学一学\(Treap\)。一直听说\(Treap\)很难,我也花了挺久才学会。
简介
\(Treap\)这个名字真的挺有内涵:
这很形象地告诉了我们:\(Treap\)是\(Tree\)(二叉搜索树)与\(Heap\)(堆)的结合体,这也是\(Treap\)能够平衡的关键。
\(Treap\)平衡的方法
\(Treap\)为什么能够平衡?它与普通的\(BST\)有什么区别?
主要就在于,它比\(BST\)多了一个优先级的设定。
首先,\(Treap\)的节点是满足\(BST\)性质的。其次,\(Treap\)的每一个节点还有一个优先级,而这些优先级又是满足堆性质的。这就能让\(Treap\)的节点保持一种随机的状态,而不会被数据卡成链(当然,脸黑也没办法)。
至于如何让它同时满足\(BST\)性质和堆性质,这放在后面再讲。
那么,该怎么确定优先级呢?
很简单,随机即可。
不过,直接用\(C++\)自带的\(rand()\)又慢又容易被卡,所以推荐手写\(rand()\),下面的代码仅供参考:
inline int Rand()
{
static ull r=2333;//static不能少,r的初值可以自己定
return (r*=233333)%=2147483647;//每次r乘上的数也可以自己定
}
\(Treap\)的基础操作
-
旋转
旋转应该是\(Treap\)最重要也是最核心的操作了。
\(Treap\)的旋转分为两种:左旋和右旋。
我们以左旋为例:
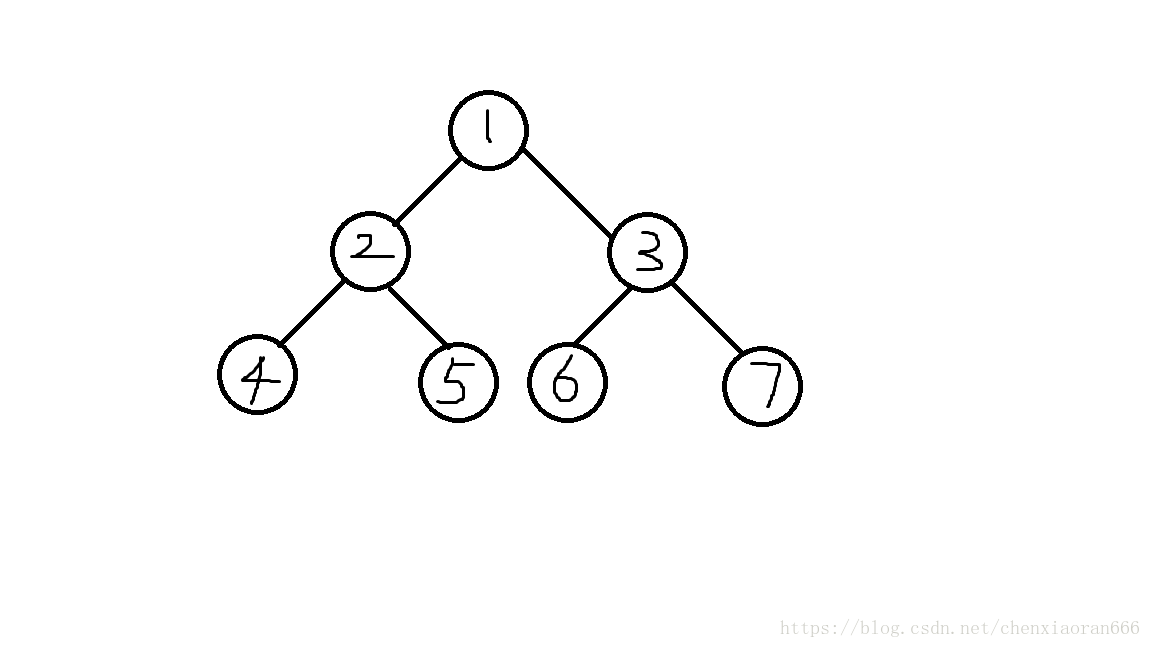
如图,是一棵需要左旋的\(Treap\)(圆圈中是节点编号而不是节点权值)。

首先,我们把根节点的右儿子改为根节点的右儿子的左儿子(右旋恰好相反)。
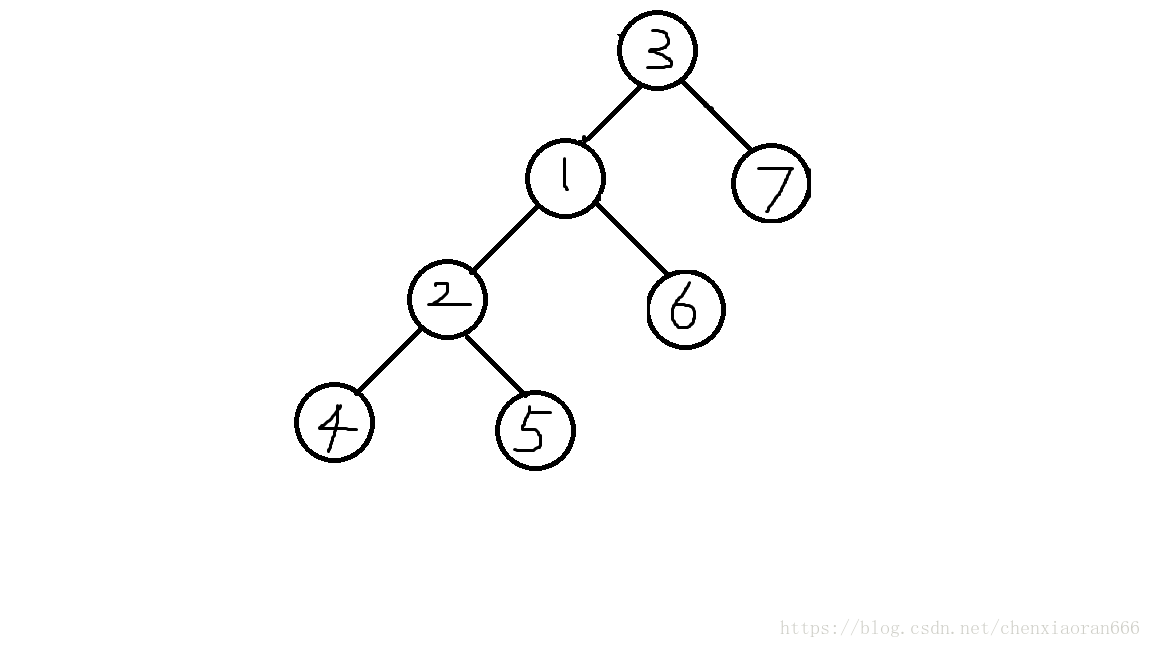
然后,再将根节点的右儿子的左儿子改为根节点,然后再将根节点改为原根节点的右儿子即可(右旋刚好相反)。
以上就是\(Treap\)的旋转操作了,但是在代码中的操作要略麻烦一点:
inline void Rotate(int &x,int d)//由于左旋和右旋的操作恰好相反,且为了避免写两段代码,我们用d=0表示左旋,d=1表示右旋
{
int k=node[x].Son[d^1];//由于左旋时用根节点的右儿子,右旋时用根节点的左儿子,所以用k存储的要与旋转方向相反
node[x].Son[d^1]=node[k].Son[d],node[k].Son[d]=x,x=k,PushUp(node[x].Son[d]),PushUp(x);//将根的与旋转方向反向的儿子改为k的与旋转方向同向的儿子,然后将k的与旋转方向同向的儿子改为根节点,并将根节点改为k,最后要记得更新节点信息
}
-
插入
\(Treap\)的插入操作与一般的\(BST\)有点像,只不过每次插入后都要比较当前节点与其儿子的优先级,从而决定是否要旋转。
代码如下:
inline void Insert(int &x,int val)//插入操作
{
if(!x) {x=Build(val);return;}//如果当前节点为空,就将元素插入这个节点
++node[x].Size;//将当前元素所在的子树大小加1
if(node[x].Val==val) ++node[x].Cnt;//如果当前元素等于插入元素,就将当前元素的个数加1
else if(node[x].Val>val)//否则如果当前元素大于插入元素
{
Insert(node[x].Son[0],val);//将插入元素插入当前元素的左子树
if(node[x].Data<node[node[x].Son[0]].Data) Rotate(x,1);//如果当前元素左儿子的优先级大于当前节点的优先级,那么就右旋(将左儿子旋到当前节点之上)
}
else//与上面类似
{
Insert(node[x].Son[1],val);
if(node[x].Data<node[node[x].Son[1]].Data) Rotate(x,0);
}
PushUp(x);//最后记得更新当前元素的信息
}
-
删除
删除\(Treap\)上的一个元素,我们要分几种情况讨论:
- 若删除元素原本存在多个,则只需将其存在个数减\(1\)即可。
- 否则,若删除元素没有子节点,则直接将这个元素赋值为\(0\)即可。
- 否则,若删除元素没有右子节点,或左子节点的优先级高于右子节点,就将以删除元素为根的子树右旋,我们可以发现,此时:原先的左子节点\(-->\)新的根节点,原先的根节点\(-->\)新的右子节点,因此,我们只要继续删除新的右子节点即可。
- 否则,就将以删除元素为根的子树左旋,继续删除新的左子节点即可(与上面类似)。
代码如下:
inline void Delete(int &x,int val)//删除值为val的数
{
if(!x) return;//如果当前节点为空节点,就退出函数
if(node[x].Val==val)//如果当前节点为要删除的节点,那就进行删除操作
{
if(node[x].Cnt>1) {--node[x].Cnt,PushUp(x);return;}//如果删除元素存在多个,就将其个数减1
if(node[x].Son[0]||node[x].Son[1])//如果当前元素有子节点
{
if(!node[x].Son[1]||node[node[x].Son[0]].Data>node[node[x].Son[1]].Data) Rotate(x,1),Delete(node[x].Son[1],val);//若删除元素没有右子节点,或左子节点的优先级高于右子节点,就将以删除元素为根的子树右旋,继续删除新的右子节点
else Rotate(x,0),Delete(node[x].Son[0],val);//否则,就将以删除元素为根的子树左旋,继续删除新的左子节点
}
else x=0;//如果当前元素没有子节点,直接将这个元素赋值为0
}
else if(node[x].Val>val) Delete(node[x].Son[0],val);//如果当前元素大于删除元素,说明删除元素在当前元素的左子树
else Delete(node[x].Son[1],val);//否则说明删除元素在当前元素的右子树
PushUp(x);//最后要记得更新当前节点的信息
}
-
询问
\(Treap\)的询问操作和普通\(BST\)没什么太大的区别,直接贴代码了:
inline int get_rank(int val)//询问值为val的数的排名
{
int x=rt,rk=0;
while(x)//只要当前节点不为空
{
if(node[x].Val==val) return node[node[x].Son[0]].Size+rk+1;//如果当前元素等于val,就可以直接返回答案了
else if(node[x].Val>val) x=node[x].Son[0];//如果当前元素大于v,则说明当前元素的排名大于val,所以访问当前元素的左子树
else rk+=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];//否则,将计数器加上当前元素的排名(不要忘记加上当前元素的存在个数),并访问当前元素的右子树
}
return rk;
}
inline int get_val(int rk)//询问排名为rk的数的值
{
int x=rt;
while(x)//只要当前节点不为空
{
if(node[node[x].Son[0]].Size>=rk) x=node[x].Son[0];//如果当前元素的排名等于rk,则返回该节点的值
else if(node[node[x].Son[0]].Size+node[x].Cnt>=rk) return node[x].Val;//否则,如果当前元素的排名大于rk,访问当前元素的左子树
else rk-=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];//不然,就将rk减去当前元素的排名,访问当前元素的右子树
}
}
inline int get_pre(int val)//询问值为val的数的前驱,也可以用get_val(get_rank(x)-1),只不过常数大一些
{
int x=rt,pre=0;
while(x)//只要当前节点不为空
{
if(node[x].Val<val) pre=node[x].Val,x=node[x].Son[1];//如果当前元素小于val,就将前驱改为当前元素,并访问当前元素的右子树
else x=node[x].Son[0];//否则,访问当前元素的左子树
}
return pre;
}
inline int get_nxt(int val)//询问值为val的数的后继,也可以用get_val(get_rank(x+1)),只不过常数大一些
{
int x=rt,nxt=0;
while(x)//只要当前节点不为空
{
if(node[x].Val>val) nxt=node[x].Val,x=node[x].Son[0];//如果当前元素大于val,就将后继改为当前元素,并访问当前元素的左子树
else x=node[x].Son[1];//否则,访问当前元素的右子树
}
return nxt;
}
- 最后,还有一个细节:
初始化时要现在平衡树中加入一个极大值和一个极小值,防止越界。
完整代码
讲了这么多,最后来一个模板:(还是以【洛谷3369】【模板】普通平衡树为例吧)
#include<bits/stdc++.h>
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define LL long long
#define swap(x,y) (x^=y,y^=x,x^=y)
#define tc() (A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++)
#define pc(ch) (pp_<100000?pp[pp_++]=(ch):(fwrite(pp,1,100000,stdout),pp[(pp_=0)++]=(ch)))
#define N 100000
int pp_=0;char ff[100000],*A=ff,*B=ff,pp[100000];
using namespace std;
int n,rt,tot=0;
struct Treap
{
int Son[2],Val,Cnt,Size,Data;
}node[N+5];
inline void read(int &x)
{
x=0;int f=1;char ch;
while(!isdigit(ch=tc())) f=ch^'-'?1:-1;
while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
x*=f;
}
inline void write(int x)
{
if(x<0) pc('-'),x=-x;
if(x>9) write(x/10);
pc(x%10+'0');
}
inline int Rand()
{
static LL r=2333;
return (r*=233333LL)%=2147483647;
}
inline void PushUp(int x)
{
node[x].Size=node[node[x].Son[0]].Size+node[node[x].Son[1]].Size+node[x].Cnt;
}
inline int Build(int val)
{
node[++tot].Val=val,node[tot].Cnt=node[tot].Size=1,node[tot].Son[0]=node[tot].Son[1]=0,node[tot].Data=Rand();
return tot;
}
inline void Init()
{
rt=Build(-2e9),node[rt].Son[1]=Build(2e9),PushUp(rt);
}
inline void Rotate(int &x,int d)
{
int k=node[x].Son[d^1];
node[x].Son[d^1]=node[k].Son[d],node[k].Son[d]=x,x=k,PushUp(node[x].Son[d]),PushUp(x);
}
inline void Insert(int &x,int val)
{
if(!x) {x=Build(val);return;}
++node[x].Size;
if(node[x].Val==val) ++node[x].Cnt;
else if(node[x].Val>val)
{
Insert(node[x].Son[0],val);
if(node[x].Data<node[node[x].Son[0]].Data) Rotate(x,1);
}
else
{
Insert(node[x].Son[1],val);
if(node[x].Data<node[node[x].Son[1]].Data) Rotate(x,0);
}
PushUp(x);
}
inline void Delete(int &x,int val)
{
if(!x) return;
if(node[x].Val==val)
{
if(node[x].Cnt>1) {--node[x].Cnt,PushUp(x);return;}
if(node[x].Son[0]||node[x].Son[1])
{
if(!node[x].Son[1]||node[node[x].Son[0]].Data>node[node[x].Son[1]].Data) Rotate(x,1),Delete(node[x].Son[1],val);
else Rotate(x,0),Delete(node[x].Son[0],val);
}
else x=0;
}
else if(node[x].Val>val) Delete(node[x].Son[0],val);
else Delete(node[x].Son[1],val);
PushUp(x);
}
inline int get_rank(int val)
{
int x=rt,rk=0;
while(x)
{
if(node[x].Val==val) return node[node[x].Son[0]].Size+rk+1;
else if(node[x].Val>val) x=node[x].Son[0];
else rk+=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];
}
return rk;
}
inline int get_val(int rk)
{
int x=rt;
while(x)
{
if(node[node[x].Son[0]].Size>=rk) x=node[x].Son[0];
else if(node[node[x].Son[0]].Size+node[x].Cnt>=rk) return node[x].Val;
else rk-=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];
}
}
inline int get_pre(int val)
{
int x=rt,pre=0;
while(x)
{
if(node[x].Val<val) pre=node[x].Val,x=node[x].Son[1];
else x=node[x].Son[0];
}
return pre;
}
inline int get_nxt(int val)
{
int x=rt,nxt=0;
while(x)
{
if(node[x].Val>val) nxt=node[x].Val,x=node[x].Son[0];
else x=node[x].Son[1];
}
return nxt;
}
int main()
{
register int i;
for(read(n),Init(),i=1;i<=n;++i)
{
int op,x;read(op),read(x);
switch(op)
{
case 1:Insert(rt,x);break;
case 2:Delete(rt,x);break;
case 3:write(get_rank(x)-1),pc('\n');break;
case 4:write(get_val(x+1)),pc('\n');break;
case 5:write(get_pre(x)),pc('\n');break;
case 6:write(get_nxt(x)),pc('\n');break;
}
}
return fwrite(pp,1,pp_,stdout),0;
}