1 作用:对于一张图求生成树数量 矩阵树定理可解决。
2 实现方式 A为邻接矩阵表示两点之间的连接关系 D为度数矩阵存放每个点的度数 根据矩阵的初等变换 基尔霍夫矩阵=D-A;
当然基尔霍夫矩阵就是拉普拉斯矩阵。
有如下几个性质:拉普拉斯矩阵的行列式为0.
拉普拉斯矩阵的任意一个余子式的行列式相等。
不连通的无向图的拉普拉斯的任意一个余子式的行列式为0。
本人行列式都不知道是什么...(很弱的
其实行列式就是一个矩阵经过规定的计算方法从而得到的一个数字,有未知数的话其实就是一个多项式,本质上是一个数值。
一阶矩阵 1*1 二阶 2*2 三阶 3*3 以此类推。
一阶矩阵的行列式=就是这个数字?! 二阶矩阵行列式=a1*b2-a2*b1; 三阶矩阵=具体图像如下。

这个定义看起来已经相当的巧妙了,却让人不算是很好求得样子。
在此之前先介绍其几何意义 1 行列式就是行列式中的行或列向量所构成的超平面多面体的有向面积或有向体积。
2 在线性变换A下的图形面积或体积的伸缩因子。
看起来第一个还是很正常的我们具体阐述第一个意义。考虑二阶行列式的几何意义。

这个好像并不是很重要叉积即是 这个平行四边形面积。当然这个几何意义也不是很重要。
余子式 对于一个n阶矩阵A 去掉第i行第j列所形成的矩阵的行列式称为这个矩阵的余子式。表示为A i j
代数余子式 Mi j =(-1)i+j Ai j
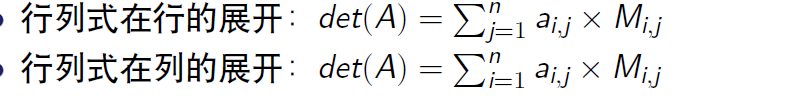
有了这些知识 那么 拉普拉斯矩阵的几个性质都是很好解决的吧。
关于拉普拉斯矩阵的性质证明 在此忽略...
考虑对拉普拉斯矩阵A的一些改变 若存在E(x,y) 那么++Ax,x ++Ay,y --Ax.y --Ay,x
那么考虑 生成树的数量 == 这个矩阵的行列的行列式
现在到了如何快速求解行列式 也就是求出下发这个式子:
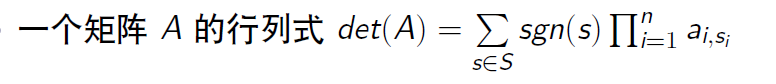
其中 sgn(s) 表示s这个排列之中的(-1)^逆序对数 如何生成这个si 看起来并不好求。
转换一个比较快速的求解方法 使用高斯消元 进行消元消成上三角矩阵,此时则有对角线上的值得乘积=行列式的值。
看的很蒙蔽对不对 其实 感性的理解相信你也已经懂了大致的做法,这部分内用 需要时间来不断沉淀。

求生成树的数量 那么 基尔霍夫矩阵也是很好列的,转换一下 高斯消元 然后求生成树数量即可。
注意 基尔霍夫矩阵是拉普拉斯矩阵的 余子式。
故我们先求出 拉普拉斯矩阵再把最后一行和最后一列消掉 最终 高斯消元。注:拉普拉斯任意一行和任意一列的余子式的行列式是相等的。
注意交换两行 那么行列式*-1;

//#include<bits/stdc++.h> #include<iomanip> #include<iostream> #include<cstdio> #include<cstring> #include<string> #include<queue> #include<deque> #include<cmath> #include<ctime> #include<cstdlib> #include<stack> #include<algorithm> #include<vector> #include<cctype> #include<utility> #include<set> #include<bitset> #include<map> #define INF 1000000000 #define ll long long #define min(x,y) ((x)>(y)?(y):(x)) #define max(x,y) ((x)>(y)?(x):(y)) #define RI register ll #define db double #define EPS 1e-8 #define mod 1000000000 using namespace std; char buf[1<<15],*fs,*ft; inline char getc() { return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++; } inline ll read() { ll x=0,f=1;char ch=getc(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getc();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getc();} return x*f; } const ll MAXN=100; ll a[MAXN][MAXN]; ll f[MAXN][MAXN]; ll n,m,cnt,ans=1; inline void add(ll x,ll y) { ++f[x][x];++f[y][y]; --f[x][y];--f[y][x]; } inline void GAUSS() { for(ll i=1;i<cnt;++i) { for(ll j=i+1;j<cnt;++j) { while(f[j][i]) { ll d=f[i][i]/f[j][i]; for(ll k=i;k<cnt;++k)f[i][k]=(f[i][k]-d*f[j][k]+mod)%mod; for(ll k=1;k<cnt;++k)swap(f[i][k],f[j][k]); ans=-ans; } } if(!f[i][i]){ans=0;return;} ans=ans*f[i][i]%mod; } ans=(ans+mod)%mod; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(ll i=1;i<=n;++i) for(ll j=1;j<=m;++j) { char c=getc(); while(c!='.'&&c!='*')c=getc(); if(c=='.')a[i][j]=++cnt; } for(ll i=1;i<=n;++i) for(ll j=1;j<=m;++j) { if(!a[i][j])continue; if(a[i+1][j])add(a[i][j],a[i+1][j]); if(a[i][j+1])add(a[i][j],a[i][j+1]); } GAUSS(); printf("%d",ans); return 0; }
