有向图
P3387 【模板】缩点
题目背景
缩点+(DP)
题目描述
给定一个(n)个点(m)条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
输入输出格式
输入格式:
第一行,(n,m)
第二行,(n)个整数,依次代表点权
第三至(m+2)行,每行两个整数(u,v),表示(u->v)有一条有向边
输出格式:
共一行,最大的点权之和。
说明
(n<=10^4,m<=10^5),点权(<=1000)
算法:(Tarjan)缩点+(DAGdp)
重点在于tarjan求解强连通分量。
定义:
- 有向图强连通分量:在有向图(G)中,如果两个顶点(v_i,v_j)间((v_i>v_j))有一条从(v_i)到(v_j)的有向路径,同时还有一条从(v_j)到(v_i)的有向路径,则称两个顶点强连通。
- 如果有向图(G)的每两个顶点都强连通,称(G)是一个强连通图。
- 有向图的极大强连通子图,称为强连通分量。
说明:单个点也可以是强联通分量。
对每个点(i)维护两个值,(dfn[i])和(low[i]),前者代表时间戳,表示(i)是第几个被访问的(用全局变量维护),后者表示最小时间,即(i)能到达的点中(dfn)最小者。
访问到点(i)时,我们先把(i)放入栈中,然后令(dfn[i]=low[i]=)当前时间,去遍历(i)点能到达的点(值得注意的是,这个点必须在栈里面),看是否能够更新(low[i])。
栈:我们求解某次强连通分量时,存储在一个强连通分量的点集。点(i)某个能遍历的点(j)在栈里面对应的即是(j)对(i)是联通的。
当(i)能到达的点遍历完毕时,若(dfn[i]!=low[i]),即它能到达一个更早的时间点,作为这个强联通分量的使点。
若(dfn[i]==low[i]),则这个点可以作为某块强连通分量的开始点。
我们把栈中的元素取出来,直到栈顶为(i),则这些取出来的点连同(i)即构成了一块强连通分量。
感性认识:用两个值维护了点的相互连通性。
我们把点缩好以后,做拓扑排序dp就行了。
code:
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int M=100010;
int min(int x,int y) {return x<y?x:y;}
int max(int x,int y) {return x>y?x:y;}
struct Edge{int to,next;}edge0[M*2],edge[M*2];
int head0[M],cnt0=0,head[M],cnt=0;
int c0[M],c[M],n,m;
void add0(int u,int v){edge0[++cnt0].next=head0[u];edge0[cnt0].to=v;head0[u]=cnt0;}
void add(int u,int v){edge[++cnt].next=head[u];edge[cnt].to=v;head[u]=cnt;}
int s[M],tot=0;
void push(int x){s[++tot]=x;}
void pop(){tot--;}
int in[M],ha[M],cntt=0,dfn[M],low[M],time=0,vis[M];
void tarjan(int now)
{
push(now);
vis[now]=1;
dfn[now]=low[now]=++time;
for(int i=head0[now];i;i=edge0[i].next)
{
int v=edge0[i].to;
if(!dfn[v]) {tarjan(v);low[now]=min(low[now],low[v]);}
else if(vis[v]) low[now]=min(low[now],dfn[v]);
}
if(dfn[now]==low[now])
{
cntt++;
while(s[tot]!=now)
{
vis[s[tot]]=0;
c[cntt]+=c0[s[tot]];
ha[s[tot]]=cntt;
pop();
}
ha[s[tot]]=cntt;
vis[s[tot]]=0;
c[cntt]+=c0[s[tot]];
pop();
}
}
queue <int > q;
int dp[M],ans=0;
void topo()
{
for(int i=1;i<=cntt;i++)
if(!in[i])
{
dp[i]=c[i];
ans=max(dp[i],ans);
q.push(i);
}
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
in[v]--;
dp[v]=max(dp[u]+c[v],dp[v]);
if(!in[v]) {ans=max(ans,dp[v]);q.push(v);}
}
}
}
int main()
{
int u,v;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",c0+i);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
add0(u,v);
}
for(int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++)
for(int j=head0[i];j;j=edge0[j].next)
{
int v=edge0[j].to;
if(ha[v]!=ha[i])
{
add(ha[i],ha[v]);
in[ha[v]]++;
}
}
topo();
printf("%d
",ans);
return 0;
}
2018.6.6
无向图
建议先看看割点的有关知识割点
补充两个概念:
1.点双连通图:若一个无向图中的去掉任意一个节点都不会改变此图的连通性,即不存在割点,则称作点双连通图
2.割点的性质:若点(u)是一个割点,则至少存在一对点(v_1,v_2),使得(v_1,v_2)的任何一个路径通过点(u)
对于割点的这个性质,我们做一个转换,若点(u)不是一个割点且它的度大于1,则对一对有一条路径经过(u)点(v_1,v_2),一定还有至少1条路径使(v_1,v_2)不经过(u)连通。再转换一下,这是不是代表(u,v_1,v_2)是一个环上的点?
我们得到了一个结论,对某度大于1的一个点(u),若它不是割点,它一定在某一个环上。
若它所在的环无割点,则这个环之间缩成一个单点。
若它所在的环有割点,假设忽略割点与环外的点相连,则可以这些割点连同非割点形成一个需要缩去的环,此时这个缩的点连的边即是这些割点向外连的边。
特别的,若这个环是一个非简单环(即自交的环,如下图)
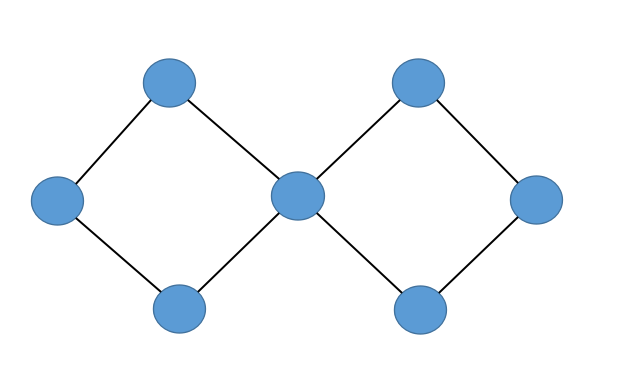
我们一般将它割成一个点,也就是说,我们缩去的是最大环。
以上两种环,不可以与点双联通分量混淆,点双联通分量是一个额外的概念,它与缩去的极大环并不可以等价。
这里不讨论点双联通分量的内容。
- 下面说说求法
我们在求解割点时,在走完每一个子树时,我们都要看看它的子树是否能够通过别的路径走到父亲之上的点,只要有一个走不上去,我们就判断它为割点。特别的,若这个点为遍历始点,我们是根据它互不连通的儿子的个数来判断它是否为割点的。
但对于极大环,我们要求出它的边界上的割点,应该怎么做呢?如果他的在某环上,并且它通过它的儿子遍历了这个环,则一定有(low[u]==dfn[u]),(u)为这个割点,也就是说,它通过它的儿子恰好只能更新到它之下的时间。这点上和上面有向图求强连通分量是差不多的。我们想有向图缩点那样,把这个环先存进栈中。
与求割点不同的是:求极大环时为了避免非简单路的影响,我们对每个割点先判断完所有的儿子,再判断条件,这点与有向图割点是一样的;割点特判了遍历始点的情况,但极大环不需要,也就是说,此“割点”并非全都是所谓严格定义的“割点”,这点对于无割点单环的情况。
与求有向图强连通分量不同的是:要特别对待父亲的那条边。
参考代码:
void tarjan(int now,int fa)
{
dfn[now]=low[now]=++time;
push(now);
used[now]=1;
for(int i=head[now];i;i=edge[i].next)
{
int v=edge[i].to;
if(v!=fa)
{
if(!dfn[v])
{
tarjan(v,now);
low[now]=min(low[now],low[v]);
}
else if(used[v])
low[now]=min(low[now],dfn[v]);
}
}
if(low[now]==dfn[now])
{
n0++;
int k;
do
{
k=s[tot];
ha[k]=n0;
used[k]=0;
pop();
}while(k!=now);
}
}
对于求法描述的对比与总结:
有向图强连通分量:
通过 某点的儿子是否能够遍历到它的判断 来判断有向图强连通分量,特别的,对于非简单环(参照无向图),我们先做完所有的子树。
无向图极大环:
通过 某点的儿子是否能够遍历到它的判断 来判断环,特别的,对于非简单环,我们先做完所有的子树;需要特判父亲来路的那条边。
两者在代码上的区别仅有是否特判父亲的来路
割点:
通过 某点的儿子是否能遍历到比它早或等于它的点来判断 是否为割点,若有任何一个儿子不满足,则为割点。特别的,可以不特判父亲,因为哪怕被父亲更新也不会超过父亲(但是判割边的时候不一样);需要特判遍历始点,通过它有没有大于2的不连通子图。
2018.6.9