期望dp

期望DP

数学期望 P=Σ（每一种状态的价值*对应的概率）
E(aX+bY)=aE(x)+bE(y)E(aX+bY)=aE(x)+bE(y)

数学期望的dp[x]一般表示到了x这一状态还差多少，最后答案是dp[0]。

期望DP步骤一般是先推数学公式，再找递推关系

1 Help Me Escape zoj3640（入门）

Now Cain is unexpectedly trapped in a cave with N paths. Due to LORD's punishment, all the paths are zigzag and dangerous. The difficulty of the ith path is ci.

Then we define f as the fighting capacity of Cain. Every day, Cain will be sent to one of the N paths randomly.

Suppose Cain is in front of the ith path. He can successfully take ti days to escape from the cave as long as his fighting capacity f is larger than ci. Otherwise, he has to keep trying day after day. However, if Cain failed to escape, his fighting capacity would increase ci as the result of actual combat. (A kindly reminder: Cain will never died.)

As for ti, we can easily draw a conclusion that ti is closely related to ci. Let's use the following function to describe their relationship:

After D days, Cain finally escapes from the cave. Please output the expectation of D.

Input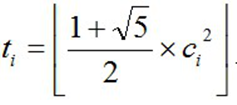

The input consists of several cases. In each case, two positive integers N and f (n ≤ 100, f ≤ 10000) are given in the first line. The second line includes N positive integers ci (ci ≤ 10000, 1 ≤ i ≤ N)

Output

For each case, you should output the expectation(3 digits after the decimal point).

Sample Input

3 1

1 2 3

Sample Output

6.889

这是我做的第一个期望题目！这题只要清楚期望计算的公式，括号别括错就行了。f[i]表示攻击力为i的期望天数，详见代码E(aX+bY)=aE(x)+bE(y)E(aX+bY)=aE(x)+bE(y)*

E(XY)=E(X)+E(Y)

var
dp:array[0..200005] of double;
c:array[0..200005]of longint;
n,x,i:longint;

 function solve(f:longint):double;
  var i:longint;
  begin
   if dp[f]>0 then exit(dp[f]);
    dp[f]:=0;
    for i:=1 to n do
       if f>c[i]{you wrong here} then
       begin
         dp[f]:=dp[f]+trunc(((1+sqrt(5))/2)*sqr(c[i]))/n; //注意向下取整，打的过，直接天数算出来+原来期望天数*
       end
            else dp[f]:=dp[f]+(1+solve(f+c[i]))/n;//1 代表花费一天+提升之后所需期望天数

      exit(dp[f]);
  end;
begin
while not eof do
 begin
   readln(n,x);
   for i:=1 to n do read(c[i]);
   fillchar(dp,sizeof(dp),0);
    writeln(solve(x):0:3);
   end;
end.

2 Race to 1 Again

Rimi learned a new thing about integers, which is - any positive integer greater than 1 can be divided by its divisors. So, he is now playing with this property. He selects a number N. And he calls this D.

In each turn he randomly chooses a divisor of D (1 to D). Then he divides D by the number to obtain new D. He repeats this procedure until D becomes 1. What is the expected number of moves required for N to become 1.

Input

Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case begins with an integer N (1 ≤ N ≤ 105).

Output

For each case of input you have to print the case number and the expected value. Errors less than 10-6 will be ignored.

Sample Input

Sample Output

Case 1: 0

Case 2: 2.00

Case 3: 3.0333333333

题解：dp[i]表示到从i除到1的期望步数

由期望定义可得dp[i]=（dp[1]+dp[S2]+dp[S3]…+dp[i]+c）/c

（S1~sn 表示i的因数，+c是因为每次走一步期望值+1，总的就是+c了），然后你会发现，这个等式中两边都有d[i]，这样是不能进行递推的，所以要进行等式化简，这样就是一个数学问题了。将dp[i]从右边提出来就是dp[i]/c，移到左边，

最后化简为

( (c - 1) / c ) * d[i] = ( d[1] + d[S2] + d[S3] + d[S4] ..... + d[Sc- 1] + c) / c;

那么d[i]就等于所有因子的期望和加上ｃ再除以ｃ-１

上代码

上代码
var
dp:array[0..100050]of double;
ans:double;
i,x,maxn,num,j,t:longint;
 begin
  for i:=2 to 100010 do
   begin
    maxn:=trunc(sqrt(i));ans:=0;num:=0;
     for j:=1 to maxn do
      begin
       if i mod j=0 then
        begin
         inc(num);
         ans:=dp[j]+ans;
          if i div j<>j then
           begin
            inc(num);
            ans:=ans+dp[i div j];
           end;
        end;

      end;
      dp[i]:=(ans+num)/(num-1);
     // if i=51 then break;
    //  writeln(i,' ',dp[i]:0:3);
   end;
 readln(t);
 for i:= 1 to t do
begin
 readln(x);
 writeln('Case ',i,': ',dp[x]:0:6);
end;、
end.

NOIP2018 rp++