【数据结构】树

目录

• 树
  • 树的性质
  • 树的存储结构
    • 双亲表示法
    • 孩子表示法
    • 孩子兄弟表示法(二叉树表示法)
  • 树和森林的遍历
    • 树的遍历
    • 森林的遍历
• 二叉树
  • 二叉树的性质
  • 二叉树的存储结构
  • 二叉树的遍历
    • 先序遍历(PreOrder)
    • 中序遍历(InOrder)
    • 后序遍历(InOrder)
    • 层次遍历(LevelOrder)
  • 线索二叉树
    • 前序线索化
    • 中序线索化
    • 线索二叉树的遍历
  • 堆
• 树和二叉树的应用
  • 二叉排序树(BST)
    • 查找
    • 插入
    • 构造
    • 删除
  • 平衡二叉树(AVL)
    • 插入
    • 查找
  • 哈夫曼树(最优二叉树)
• 常用算法
  • 层次遍历的应用
  • 后序遍历的应用

(ElemType*)malloc(sizeof(ElemType)*InitSize);
此函数是一个指针型函数，返回的指针指向该分配域的开头位置。

树

树的性质

• 树中的结点数 = 所有结点的度数 + 1
• 度为m的树中第i层上至多有(m^{i-1})个结点(i>=1)
• 高度为h的m叉树至多有((m^h-1)/(m-1))个结点（推导公式S=(m^{h-1}+m^{h-2}+m^{h-3}+...+m+1)=((m^h-1)/(m-1))）
• 具有n个结点的m叉树的最小高度为(⌈log_m(n(m-1)+1)⌉)
• 按结点数的和算：总结点数(N=n_0+n_1+n_2+...+n_m)（结点数的和）（树的度为m，即 m叉树）
• 按度数算：总结点数(N=n_1+2n_2+3n_3+...+mn_m+1)（度数+1）
• 由上面两个式子可得，(n_0=1+n_2+2n_3+3n_4+...+(m-1)n_m)

树的存储结构

双亲表示法

双亲表示法采用一组连续空间来存储每个结点，同时在每个结点中增设一个伪指针，指示其双亲结点在数组中的位置。根结点下标为0，其伪指针域为-1.

• 存储结构；

//双亲表示法
#define MAX_TREE_SIZE 100   //树中最多结点数
typedef struct {        //树的结点定义
    ElemType data;      //数据元素
    int parent;         //双亲位置域
}PTNode;
typedef struct {        //树的类型定义
    PTNode nodes[MAX_TREE_SIZE];    //双亲表示
    int n;              //结点数
}PTree;     //Parent Tree

• 优点：
  可以很快得到每个结点的双亲结点
• 缺点：
  但求结点的孩子时需要遍历整个结构

孩子表示法

孩子表示法是从树的根节点开始，使用顺序表依次存储树中各个节点，将每个结点的孩子结点都用单链表链接起来形成一个线性结构，用于存储各节点的孩子节点位于顺序表中的位置，此时n个结点就有n个孩子链表(叶子结点的孩子链表为空表)。

• 存储结构；

//孩子表示法
typedef struct CTNode{
    int child;//链表中每个结点存储的不是数据本身，而是数据在数组中存储的位置下标
    struct CTNode * next;
}ChildPtr;
typedef struct {
    TElemType data;//结点的数据类型
    ChildPtr* firstchild;//孩子链表的头指针
}CTBox;
typedef struct{
    CTBox nodes[MAX_SIZE];//存储结点的数组
    int n,r;//结点数量和树根的位置
}CTree;     //Child Tree

• 优点：
  寻找子女的操作非常直接
• 缺点：
  而寻找双亲的操作需要遍历n个结点中孩子链表指针域所指向的n个孩子链表

孩子兄弟表示法(二叉树表示法)

孩子兄弟表示法（左孩子右兄弟）以二叉链表作为树的存储结构。使每个结点包括三部分内容：结点值、指向结点第一个孩子结点的指针，及指向结点下一个兄弟结点的指针(沿此域可以找到结点的所有兄弟结点)。

• 存储结构：

//孩子兄弟表示法
typedef struct CSNode {
    ElemType data;      //数据域
    struct CSNode *firstchild, *nextsibling;    //第一个孩子和右兄弟指针
}CSNode, *CSTree;   //Child Sibling Tree

• 优点：
  可以方便地实现树转换为二叉树的操作，易于查找结点的孩子结点等
• 缺点：
  从当前结点寻找其双亲结点比较麻烦。若为每个结点增设一个parent域指向其父节点，则查找结点的父节点也很方便。

树和森林的遍历

与二叉树遍历的对应关系

树	森林	二叉树
先根遍历	先序遍历	先序遍历
后根遍历	中序遍历	中序遍历

树的遍历

• 先根遍历：
  若树非空，则先访问根节点，再按从左到右的顺序遍历根结点的每棵子树，其访问顺序与这棵树相应的二叉树的先序遍历循序相同。
  先序遍历(NLR)->先根遍历(根 孩子 兄弟)

• 后根遍历：
  若树非空，则按从左到右的顺序遍历根结点的每棵子树，之后再访问根节点。其访问顺序与这棵树相应的二叉树的中序遍历循序相同。
  中序遍历(LNR)->后根遍历(孩子 根 兄弟)

森林的遍历

• 先序遍历森林。若森林为非空，则按如下规则进行遍历：
  • 访问森林中第一棵树的根节点。
  • 先序遍历第一棵树中根节点的子树森林。
  • 先序遍历除去第一棵树之后剩余的树构成的森林。
• 中序遍历森林。若森林为非空，则按如下规则进行遍历：
  • 中序遍历第一棵树中根节点的子树森林。
  • 访问森林中第一棵树的根节点。
  • 中序遍历除去第一棵树之后剩余的树构成的森林。

二叉树

二叉树的性质

• 非空二叉树上的叶子结点数 = 度为2的结点数 + 1，即 (n_0 = n_2 + 1)（叶子当然比分支多啊，类比一下现实中的树）
• 非空二叉树上第k层上至多有(2^{k-1})个结点(k$>=$1)
• 高度为h的二叉树至多有(2^h-1)个结点(h>=1)
• 对完全二叉树按从上到下、从左到右的顺序依次编号1,2,...,n，则对结点i有以下关系：
  • 所在层次为(⌊log_2i⌋ + 1)
  • 双亲结点编号为⌊(i/2)⌋
  • 左孩子结点编号为2i

  • 右孩子结点编号为2i+1

    PS:若越界则不存在。
    这个性质也是二叉树（堆）的顺序存储下标从1开始的理由。

• 具有n个(n>0)结点的完全二叉树的高度为(⌈log_2(n+1)⌉)或(⌊log_2n + 1⌋)
• 在有n个结点的二叉树中，有n+1个空指针
• 在有n个结点的二叉树中，有n-1个度（即 边，一个度为一个边）（除了根结点，其他结点都是边+结点）
• 完全二叉树(n_1)只能等于0或1
• 哈夫曼树由于其构造方法，所以只有度为0和度为2的结点（(n_1)=0）
• (N=n_0+n_1+n_2=n_1+2n_2+1)

二叉树的存储结构

• 顺序存储结构：
  • 注意：要从数组下标为1开始存储树中的结点（若从0开始存，则不满足上述完全二叉树的结点关系性质）

  • 适用于完全二叉树（堆）和满二叉树

    注意区别树的顺序存储结构与二叉树的顺序存储结构，在树的顺序存储结构（双亲表示法）中，数组下标代表结点的编号，下标上所存的内容指示了结点之间的关系；而在二叉树的顺序存储结构中，数组下标既代表了结点的编号，又指示了树中各结点之间的关系。

• 链式存储结构：
  • 数据域 + 左右指针域

二叉树的遍历

注意：中序和后序遍历，都是出容器时 遍历访问，进入容器只是存放遍历结点的顺序。
先序遍历是访问后，入容器

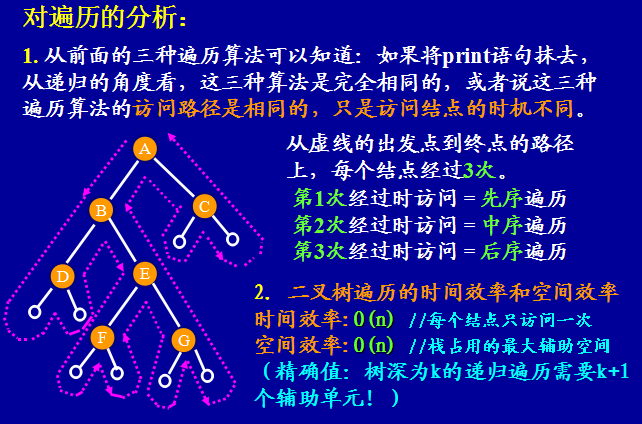
遍历二叉树其实是以一定的规则，将二维的二叉树中的结点排列成一个线性序列，其实质是对一个非线性结构进行线性化操作，使这个访问序列中的每个结点（第一个和最后一个除外）都有一个直接前驱和直接后继。

注意：这三种遍历算法的访问路径是相同的(都是围着树的外圈访问一整圈)，只是访问结点的时机不同。(先序遍历第一次经过就访问，中序遍历第二次经过才访问，后序遍历第三次经过才访问。加上左右分支，沿着树的外圈访问)，可以以此来求某一结点的前驱后继。但要求整体的前驱后继，还是将整个二叉树生成遍历序列。

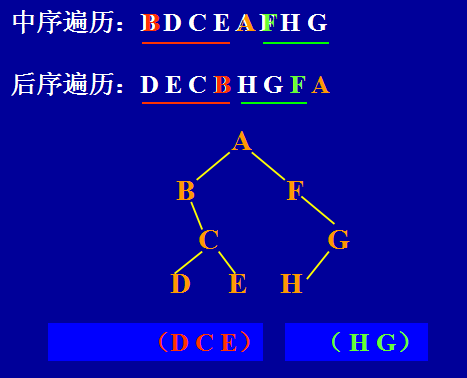
• 由二叉树的先序序列和中序序列（或 后序序列和中序序列）可以唯一地确定一棵二叉树。
  由先（后）序序列可以得知根结点，再由中序序列可以根据根结点划分左右子树；
  再由先（后）序序列得知左右子树根结点，再中序划分。。
  

我们以下的使用的栈或队列都是作为一个工具来解决其他问题的，我们可以把栈或队列的声明和操作写的很简单，而不必分函数写出。

• 顺序栈
  1. 声明一个栈并初始化：

    ElemType stack[maxSize];    //存放栈中的元素
    int top = -1;   //栈顶指针（指向栈顶元素）

  1. 元素进栈：

    stack[++top] = x;

  1. 元素出栈：

    x = stack[top--];

  1. 判断栈空

    top == -1;  //栈空
    top > -1;   //栈非空

• 顺序队列
  1. 声明一个队列并初始化：

    ElemType queue[maxSize];    //存放队列中元素
    int front = -1, rear = -1;  //队头（指向队头元素的前一个位置），队尾（指向队尾元素）

  1. 元素入队：

    queue[++rear] = x;

  1. 元素出队：

    x = queue[++front];

  1. 判断队空

    front == rear;  //队空
    front < rear;   //队非空

先序遍历(PreOrder)

左右都是经过，根才访问。

• 操作过程：
  简称，根左右
  若二叉树为空，则什么也不做；否则，
  1. 访问根节点；
  2. 先序遍历左子树；
  3. 先序遍历右子树。
• 具体实现：
  • 递归算法：

  void PreOrder(BiTree T) {
    if(T == NULL) {         //合法性检验
        return;
    }
    visit(T);               //访问根节点
    PreOrder(T->lchild);    //递归遍历左子树
    PreOrder(T->rchild);    //递归遍历右子树
  }

  • 非递归算法：

  //二叉树先序遍历的非递归算法，算法需要借助一个栈
  void PreOrder2(BiTree T) {
    InitStack(S);       //初始化栈
    BiTNode *p = T;     //p是遍历指针
    while(p || !IsEmpty(S)) {   //p不空 或 栈中还有元素时循环
        if(p) {                 //根节点进栈，遍历左子树
            visit(p);
            Push(S, p);         //每遇到非空二叉树先向左走
            p = p->lchild;
        }else {                 //根指针出栈，访问根节点，遍历右子树
            Pop(S, p);          //出栈，访问根节点
            p = p->rchild;      //再向右子树走
        }
    }
  }

中序遍历(InOrder)

左右都是经过，根才访问。

• 操作过程：
  简称，左根右

• 具体实现：
  • 递归算法：

  void InOrder(BiTree T) {
    if(T == NULL) {
        return;
    }
    InOrder(T->lchild);
    visit(T);
    InOrder(T->rchild);
  }

  • 非递归算法：
    借助栈，可以将二叉树的递归遍历算法转换为非递归算法。
    先扫描（并非访问）根节点的所有左节点，并将它们一一进栈，然后出栈一个结点*p（显然结点*p没有左孩子结点或左孩子结点均已被访问过），访问它。然后扫描该结点的右孩子结点，将其进栈，再扫描该右孩子结点的所有左结点并一一进栈，如此继续，直到栈空为止。

  //二叉树中序遍历的非递归算法，算法需要借助一个栈
  void InOrder2(BiTree T) {
    InitStack(S);       //初始化栈
    BiTNode *p = T;     //p是遍历指针
    while(p || !IsEmpty(S)) {   //p不空 或 栈中还有元素时循环
        if(p) {                 //根节点进栈，遍历左子树
            Push(S, p);         //每遇到非空二叉树先向左走
            p = p->lchild;
        }else {                 //根指针出栈，访问根节点，遍历右子树
            Pop(S, p);          //出栈，访问根节点
            visit(p);
            p = p->rchild;      //再向右子树走
        }
    }
  }

后序遍历(InOrder)

左右都是经过，根才访问。

• 操作过程：
  简称，左右根

• 具体实现：
  • 递归算法：

  void PostOrder(BiTree T) {
    if(T == NULL) {
        return;
    }
    PostOrder(T->lchild);
    PostOrder(T->rchild);
    visit(T);
  }

  • 非递归算法：
    后序非递归遍历二叉树的顺序是是先访问左子树，再访问右子树，最后访问根结点。当用堆栈来存储结点时，必须分清返回根结点时是从左子树返回的还是从右子树返回的。所以，使用辅助指针r，其指向最近访问过的结点。也可在结点中增加一个标志域，记录是否已被访问。
    

  void PostOrder(BiTree T) {
    InitStack(S);
    p = T;
    r = NULL;       //r指向最近访问过的结点
    while(p || !IsEmpty(S)) {
        if(p) {         //走到最左边
            push(S, p);
            p = p->lchild;
        }else {         //向右
            GetTop(S, p);   //取栈顶结点
            if(p->rchild && p->rchild!=r) { //若右子树存在，且未被访问过
                p = p->rchild;  //转向右
            }else {             //否则，弹出结点并访问
                pop(S, p);      //将结点弹出
                visit(p->data); //访问该结点
                r = p;          //记录最近访问过的结点
                p = NULL;       //结点访问完后，重置p指针，用于再次循环（从栈内结点开始）
            }
        }
    }
  }

因为直到最后才访问根结点，所以访问到值为x的结点时，上面的所有祖先根结点都还没被访问，栈中所有元素均为该结点的祖先，依次出栈打印即可。

迭代后序遍历访问一个结点*p时，栈中结点恰好是*p结点的所有祖先。从栈底到栈顶结点再加上*p结点，刚好构成从根结点到*p结点的一条路径。再很多算法设计中都利用了这一特性求解，如求根结点到某结点的路径、求两个结点的最近公共祖先等，都可以利用这个思路来实现。

这三种遍历算法中，递归遍历左右子树的顺序都是固定的，只是访问根结点的顺序不同。不管采用哪种遍历算法，每个结点都访问一次且仅访问一次，故时间复杂度都是O(n)。

在递归遍历中，递归工作栈的栈深恰好为树的深度，所以在最坏情况下，二叉树是有n个结点且深度为n的单支树，遍历算法的空间复杂度为O(n)。

层次遍历(LevelOrder)

• 操作过程：
  要进行层次遍历，需要借助一个队列。先将二叉树根结点入队，然后出队，访问该结点，若它有左子树，则将左子树根结点入队；若它有右子树，则将右子树根结点入队。然后出队，对出队结点访问，如此反复，直到队列为空。

• 具体实现：

void LevelOrder(BiTree T) {
    InitQueue(Q);       //初始化辅助队列
    BiTNode *p;
    EnQueue(Q, T);      //将根结点入队
    while(!IsEmpty(Q)) {    //队列不空循环
        DeQueue(Q, p);      //队头元素出队，出队指针才是用来遍历的遍历指针
        visit(p);           //访问当前p所指向结点
        if(p->lchild != NULL) { //左子树不空，则左子树入队列
            EnQueue(Q, p->lchild);
        }
        if(p->rchild != NULL) { //右子树不空，则右子树入队列
            EnQueue(Q, p->rchild);
        }
    }
}

用层次遍历易于找到某结点的父结点。而且层次遍历采用迭代效率高，迭代方法也方便实现。

线索二叉树

传统的链式存储仅能体现一种父子关系，不能直接得到结点在遍历中的前驱或后继。在二叉链表表示的二叉树中存在大量的空指针(n-1个)，利用这些空链域存放指向其直接前驱或后继的指针，即可成为线索二叉树。

在有n个结点的二叉树中，有n+1个空指针。这是因为每个叶结点有2个空指针，而每个度为1的结点有1个空指针，所以总的空指针数为(2n_0+n_1)，又有(n_0=n_2+1)，所以总的空指针为(n_0+n_1+n_2+1=n+1)

注意：线索二叉树指明了在存储过程中的数据存放方式，所以它是一种物理结构。

• 目的：
  为了加快查找结点前驱和后继的速度（加快对二叉树的遍历）。
  线索二元树的左线索指向其前驱，右线索指向其后继。

• 存储结构：

//线索二叉树
typedef struct ThreadNode {     //线索二叉树结点
    ElemType data;      //数据元素
    struct ThreadNode *lchild, *rchild;     //左、右孩子指针
    int ltag, rtag;     //左、右线索标志
    //tag=0代表child指针指向孩子，tag=1代表child指针指向前驱后继
}ThreadNode, *ThreadTree;

以这种结点结构构成的二叉链表作为二叉树的存储结构，称为线索链表；
其中指向结点前驱和后继的指针称为线索；
加上线索的二叉树称为线索二叉树；
对二叉树以某种遍历使其变为线索二叉树的过程称为线索化。

前序线索化

• 具体实现：
  通过前序遍历对二叉树线索化的递归算法如下：

//前序遍历对二叉树线索化的递归算法
void PreThread(ThreadTree &p, ThreadTree &pre) {
//指针pre指向前序遍历时上一个刚刚访问过的结点，用它来表示各结点访问的前后关系
    if(!p) {    //递归出口
        return;
    }
    
    //下面开始建立线索化（其实就相当于遍历中的 “访问” ）
    if(p->lchild == NULL) {     //左子树遍历到头，左子树为空，“建立前驱线索”
        p->lchild = pre;
        p->ltag = 1;
    }
    if(pre!=NULL && pre->rchild==NULL) {    //“建立前驱结点的后继线索”
        pre->rchild = p;        //“建立前驱结点的后继线索”（仅建立了前驱的后继线索，所以最后一个结点的后继线索没有建立）
        pre->rtag = 1;
    }
    pre = p;                    //标记当前结点称为刚刚访问过的结点(注意：访问!=扫描)
    //访问是指对该结点进行操作(如print输出)，而扫描则代表只是经过了这个结点，并没有执行任何操作
    
    PreThread(p->lchild, pre);  //递归线索化左子树
    PreThread(p->rchild, pre);  //递归，线索化右子树
}

---

//通过前序遍历建立前序线索二叉树
void CreatePreThread(ThreadTree T) {
    ThreadTree pre = NULL;
    if(!T) {
        return;
    }
    PreThread(T, pre);      //线索化二叉树，没有建立最后一个结点的后继线索
    pre->rchild = NULL;     //处理遍历的最后一个结点
    pre->rtag = 1;
}

中序线索化

• 操作过程：
  对二叉树的线索化，实质上就是遍历一次二叉树，只是在遍历的过程中，检查当前结点左右指针域是否为空，若为空，将它们改为指向前驱结点或后继结点的线索。

• 具体实现：
  通过中序遍历对二叉树线索化的递归算法如下：

//中序遍历对二叉树线索化的递归算法
void InThread(ThreadTree &p, ThreadTree &pre) {
//指针pre指向中序遍历时上一个刚刚访问过的结点，用它来表示各结点访问的前后关系
    if(!p) {    //递归出口
        return;
    }
    InThread(p->lchild, pre);   //递归线索化左子树
    
    //下面开始建立线索化（其实就相当于遍历中的 “访问” ）
    if(p->lchild == NULL) {     //左子树遍历到头，左子树为空，建立前驱线索
        p->lchild = pre;
        p->ltag = 1;
    }
    if(pre!=NULL && pre->rchild==NULL) {
        pre->rchild = p;        //建立前驱结点的后继线索（仅建立了前驱的后继线索，所以最后一个结点的后继线索没有建立）
        pre->rtag = 1;
    }
    pre = p;                    //标记当前结点称为刚刚访问过的结点(注意：访问!=扫描)
    //访问是指对该结点进行操作(如print输出)，而扫描则代表只是经过了这个结点，并没有执行任何操作
    
    InThread(p->rchild, pre);   //递归，线索化右子树
}

---

//通过中序遍历建立中序线索二叉树
void CreateInThread(ThreadTree T) {
    ThreadTree pre = NULL;
    if(!T) {
        return;
    }
    InThread(T, pre);       //线索化二叉树，没有建立最后一个结点的后继线索
    pre->rchild = NULL;     //处理遍历的最后一个结点
    pre->rtag = 1;
}

线索化后，先序线索二叉树可以很简单的找到一个结点的先序后继，而查找先序前驱必须知道该结点的双亲结点；
中序线索二叉树可以找到一个结点的中序前驱与中序后继；
后序线索二叉树可以找到一个结点的后序前驱，而查找后序后继也必须知道该结点的双亲结点。

线索二叉树的遍历

中序线索化二叉树主要是为访问运算服务的，这种遍历不再需要借助栈，因为他的结点中隐含了线索二叉树的前驱和后继信息。利用线索二叉树，可以实现二叉树遍历的非递归算法。

1. 求中序线索二叉树中中序下的第一个结点：

ThreadNode *Firstnode(ThreadNode *p) {
    while(p->ltag == 0) {   //最左下的结点(不一定是叶结点)
        p = p->lchild;
        return p;
    }
}

1. 求中序线索二叉树中结点p在中序序列下的后继结点：

ThreadNode *Nextnode(ThreadNode *p) {
    if(p->rtag == 0) {      //有右子树
        return Firstnode(p->rchild);    //找右子树的最左下结点(即为后继节点)(手动找)
    }else {     //rtag==1 直接返回后继线索
        return p->rchild;   //(根据线索自动找)
    }
}

1. 中序线索二叉树的中序遍历算法：

void Inorder(ThreadNode *T) {
    //从中序下第一个结点(最左下结点)开始，依次找其后继节点
    for(ThreadNode *p=Firstnode(T); p!=NULL; p=Nextnode(p)) {
        visit(p);
    }
}

堆

优先队列(Priority Queue)：特殊的“队列”，取出元素的顺序是按照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序。

使用数组或链表的话效率不高，所以我们试着采用二叉树来实现优先队列，所以我们引入了“堆”。

• 基本概念：
  堆可以看成是一棵完全二叉树，特点是父亲大孩子小，或者父亲小孩子大，前者称为大顶堆，后者称为小顶堆。

注意:从根结点到任意结点路径上的结点序列具有有序性。所以堆的插入和删除都是沿着有序的轨迹进行操作。
堆经常被用来实现优先级队列，优先级队列在操作系统的作业调度和其他领域有着广泛的应用。

树和二叉树的应用

二叉排序树(BST)

二叉排序树作为一种动态集合，其特点是树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键值等于给定值得结点时再进行插入的。

• 二叉排序树(Binary Sort Tree)的定义：
  • 若左子树非空，则左子树上所有关键字值均小于根节点关键字值。
  • 若右子树非空，则右子树上所有关键字值均大于根节点关键字值。

  • 左、右子树本身也分别是一棵二叉排序树。

    注意：二叉排序树的插入必为一个新的叶子结点。

左子树结点值 < 根结点值 < 右子树结点值 (没有相等值)
所以对二叉排列树进行中序遍历，可以得到一个递增的有序序列。

当有序表是静态查找表时，宜用顺序表作为其存储结构，而采用二分查找实现其查找操作；若有序表是动态查找表，则应选择二叉排序树作为其逻辑结构。

查找

• 操作过程：
  二叉排序树的查找是从根节点开始，沿着某个分支逐层向下进行比较的过程。
  若二叉排序树非空，则将给定值与根节点的关键字比较，若相等，则查找成功；若给定值小于根节点的关键字，则在根节点的左子树查找；若给定值大于根节点的关键字，则在根节点的右子树查找。

• 具体实现：
  • 递归实现：

  BSTNode *BST_Search(BiTree T, ElemType key) {
    if(!T) {
        return NULL;
    }
    if(key < T->data) {
        return BST_Search(key, T->lchild);
    }else if(key > T->data) {
        return BST_Search(key, T->rchild);
    }else {     //相等
        return T;
    }
  }

  • 非递归实现：

  //查找函数返回指向关键字值为key的结点指针，若不存在，返回NULL
  BSTNode *BST_Search(BiTree T, ElemType key, BSTNode *&p){
    p = NULL;   //p指向被查找结点的双亲，用于插入和删除操作中
    while(T!=NULL && key!=T->data) {
        p = T;
        if(key < T->data) {
            T = T->lchild;
        }else {
            T = T->rchild;
        }
    }
    return T;
  }

插入

• 操作过程：
  若原二叉排序树为空，则直接插入结点；否则，若关键字k小于根结点关键字，则插入左子树，若关键字k大于根结点关键字，则插入右子树。

• 具体实现：

//在二叉排序树T中插入一个关键字为k的结点
int BST_Insert(BiTree &T, ElemType k) {
    if(T == NULL) {     //原树为空，新插入的记录为根结点
        T = (BiTree)malloc(sizeof(BSTNode));
        T->data = k;
        T->lchild = NULL;
        T->rchild = NULL;
        return 1;       //插入成功
    }else if(k == T->data) {    //树中存在相同关键字的结点
        return 0;
    }else if(k < T->data) {     //插入T的左子树
        return BST_Insert(T->lchild, k);
    }else {                     //插入T的右子树
        return BST_Insert(T->rchild, k);
    }
}

构造

• 操作过程：
  每读入一个元素，就建立一个新结点，若二叉排序树为空，则将新结点作为二叉排序树的根结点；若二叉排序树为非空，则将新结点的值域根结点的值比较，若小于根结点的值，则插入左子树，否则插入右子树。
  其实就是，依次输入数据元素，并将它们插入二叉排序树中适当位置上的过程。

• 具体实现：

//用关键字数组str[]建立一个二叉排序树
void Creat_BST(BiTree &T, ElemType str[], int n) {
    T = NULL;       //初始时bt为空树
    int i = 0;
    while(i < n) {  //依次将每个元素插入
        BST_Insert(T, str[i]);
        i++;
    }
}

删除

在二叉排序树中删除一个结点时，不能把以该结点为根的子树上的结点都删除，必须先把被删除结点从存储二叉排序树的链表摘下，将因删除结点而断开的二叉链表重新链接起来，同时确保二叉排序树的性质不会丢失。

• 操作过程：
  1. 若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。
  2. 若结点z只有一棵左子树或右子树，则让z的子树称为z父节点的子树，替代z的位置。
  3. 若结点z有左、右两棵子树，则令z的直接后继(或直接前驱)(即右子树中的最小元素(或左子树中最大元素))替代z，然后从二叉排序树中删去这个直接后继(或直接前驱)，这样就转换成了第一或第二种情况。
• 具体实现：

//查找最小元素的递归函数
BiTree FindMin(BiTree T) {
    if(!T) {    //空的二叉搜索树
        return NULL;
    }
    if(!T->lchild) {    //找到最左孩子结点并返回
        return T;
    }else {
        return FindMin(T->lchild);  //沿着左子树继续找
    }
}

//查找最大元素的迭代函数
BiTree FindMax(BiTree T) {
    if(!T) {    //空的二叉搜索树
        return NULL;
    }
    while(T->rchild) {  //找到最右孩子结点
        T = T->rchild;
    }
    return T;
}

//删除二叉排序树中值为x的结点
BiTree Delete(ElemType x, BiTree T) {
    BiTree tmp;
    if(!T) {
        printf("要删除的元素未找到");
    }
    if(x < T->data) {
        T->lchild = Delete(x, T->lchild);   //左子树递归删除
    }else if(x > T->data) {
        T->rchild = Delete(x, T->rchild);   //右子树递归删除
    }else {
        if(T->lchild && T->rchild) {        //被删除结点有左右两个子结点
            tmp = FindMin(T->rchild));      //在右子树中找最小元素填充删除结点
            T->data = tmp->data;
            T->rchild = Delete(T->data, T->rchild);//在删除结点的右子树中删除最小元素
        }else {     //被删除结点有一个或没有子结点
            tmp = T;
            if(!T->lchild) {    //没有左孩子
                T = T->rchild;
            }else if(!T->rchild) {  //没有右孩子 
                T = T->lchild;
            }
            free(tmp);
        }
    }
    return T;
}

平衡二叉树(AVL)

为避免树的高度增长过快，降低二叉排序树的性能，规定在插入和删除二叉树结点是，要保证任意结点的左右子树高度差的绝对值不超过1，将这一的二叉树称为平衡二叉树(Balanced Binary Tree)，简称平衡树(AVL)。

平衡因子：结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只可能是-1、0、1。

插入

• 操作过程：
  每当在二叉排序树中插入（或删除）一个结点时，首先检查其插入路径上的结点是否因为此次操作而导致了不平衡。若导致了不平衡，则先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A，再对A为根的子树，再保持二叉排序树的前提下，调整各结点的位置关系，使之重新达到平衡。

每次调整的对象都是最小不平衡子树，即以插入路径上离结点最近的平衡因子的绝对值大于1的结点作为根的子树。

将最小不平衡子树的三个节点按大小列出排序，调整三个结点（爷子孙三代）（LL,RR,LR,RL），调整成父、左孩子、右孩子，调整完毕后，将剩下的结点（小于等于四个，因为调整完毕后只有两层，现在加入第三层）顺着接到下面（若不清楚怎么顺着接，可以将其分支画出来，补充到四个，从左到右接上去就好了（空节点也要接上去））。

• LL：（三个结点：X<k1<k2）（中间大小的结点提出，另外两个放左右）
  
• RR：（三个结点：k1<k2<Z）
  
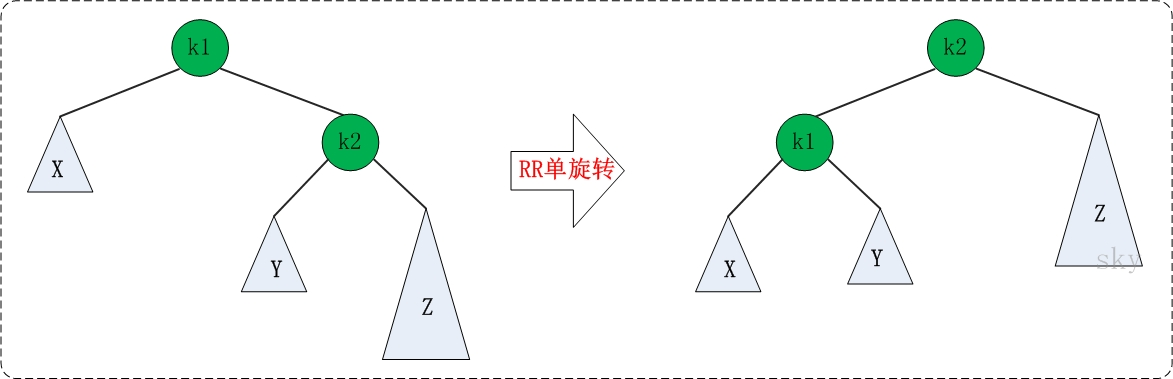
• LR：（三个结点：k1<k2<k3）（中间大小的结点提出，另外两个放左右）（孙子(k2)提出，比较另外两个，放左右）
  
• RL：（三个结点：k1<k2<k3）
  

查找

查找过程中，与给定值进行比较的关键字个数不超过树的深度。

• 性质：
  假设以(n_h)表示深度为h的平衡树中含有的最少结点数。显然，有(n_0)=0,(n_1)=1,(n_2)=2,并且有(n_h=n_{h-1}+n_{h-2}+1)。

哈夫曼树(最优二叉树)

在许多实际应用中，树中结点常常被赋予一个表示某种意义的数值，称为该结点的权。
从树的根结点到任意节点的路径长度（经过的边数）与该结点上权值的乘积，称为该结点的带权路径长度。
树中所有结点的带权路径长度之和称为该树的带权路径长度(WPL)。

• WPL=∑路径*结点权值=非叶子结点的权值之和
• 性质：
  1. 每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。
  2. 构造过程中共新建了n-1个结点(双分支结点)，因此哈夫曼树中的结点总数为2n-1。
  3. 每次构造都选择2棵树作为新结点的孩子，因此哈夫曼树中不存在度为1的结点。((n_1)=0)
  4. 字符 <-> 编码 <-> 叶子结点，一一对应。
• 构造：
  • 在n个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
  • 那两个最小权值的合并为如今这个新的权值；
  • 即，在原有的n个权值中删除那两个最小的权值，同时将新的权值加入到n–2个权值的行列中，以此类推；

  • 重复（1）和（2），直到所有的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。
    

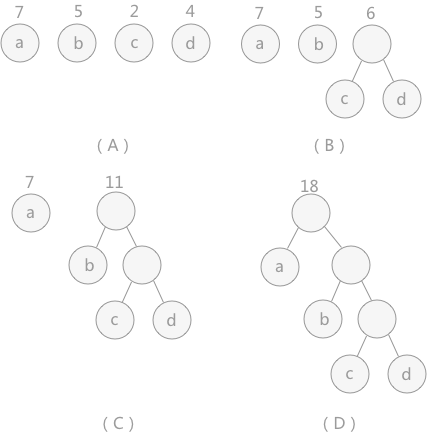
    注意：构建时，不要抓着那棵合成的树一直构建，当该树合成到一定程度，它就不是最小的权值了。

哈夫曼编码时，0和1究竟是表示左子树还是表示右子树没有明确规定。因此，左、右结点的顺序是任意的，所以构造出的哈夫曼树并不唯一，但各哈夫曼树的带权路径长度(WPL, Weighted Path Length)相同且为最优。

常用算法

层次遍历的应用

求树高

• 设计思想：
  采用层次遍历的算法，设置变量level记录当前结点所在的层数，设置变量last指向当前层的最右结点，每次层次遍历出队时与last比较，若两者相等，则层数+1，并让last指向下一层的最右结点，直到遍历完成。

  出队指针用来访问遍历（遍历指针），出队遇到最右结点层数+1，其实也可以遇到下层第一个结点+1，但是不好记录第一个结点。

• 算法：

int Btdepth(BiTree T) {
    if(!T) {
        return 0;
    }
    int front = -1, rear = -1;      //队头队尾，队头指向队头元素的前一个位置，队尾指向队尾元素
    int last = 0, level = 0;        //last指向下一层的最右结点
    BiTree Q[MaxSize];              //设置队列Q，元素是二叉树结点指针且容量足够
    Q[++rear] = T;                  //将根结点入队
    BiTree p;
    //其实层次遍历，是队头指针遍历(出队时访问)，队尾指针只是负责增加元素
    while(front < rear) {           //队不空
        p = Q[++front];             //队列元素出队
        if(p->lchild) {
            Q[++rear] = p->lchild   //左孩子入队
        }
        if(p->rchild) {
            Q[++rear] = p->rchild;  //右孩子入队
        }
        if(front==last) {           //处理该层的最右结点，front指向该层刚出队的最右节点，遇到最右结点层数+1
            level++;                //层数+1
            last = rear;            //last指向下层
        }
    }
    return level;
}

//递归
int Btdepth2(BiTree T) {
    if(!T) {
        return 0;
    }
    ldep = Btdepth2(T->lchild); //左子树高度
    rdep = Btdepth2(T->rchild); //右子树高度
    if(ldep > rdep) {
        return ldep+1;      //树的高度为子树最大高度加根结点
    }else {
        return rdep+1;
    }
}

---

求树宽

• 设计思想：
  采用层次遍历的方法求出所有结点的层次，并将所有结点和对应的层次放在一个队列中，然后通过扫描队列求出各层的结点总数，最大的层结点总数即为二叉树的宽度。

  MY：采用层次遍历的方法，设置宽度变量width记录宽度，max记录最大宽度，设置变量last指向当前层的最右结点，每次层次遍历出队时宽度+1 ，再与last指针比较，若两者相等（即遍历到最右结点），则width与max比较，用max记录下当前最大宽度，并将宽度清零，last指向下一层的最右结点。
• 算法：

    int BTWidth(BiTree b) {
        BiTree p;
        int last = 0, width = 0, max = 0;
        
        BiTree queue[MaxSize];
        int front = -1, rear = -1;
        
        queue[++rear] = b;      //根结点入队
        while(front < rear) {
            p = queue[++front]; //出队
            width++;    //宽度+1
            if(p->lchild) {
                queue[++rear] = p->lchild;
            }
            if(p->rchild) {
                queue[++rear] = p->rchild;
            }
            if(front == last) {     //遍历到最右结点
                if(width > max) {
                    max = width;    //记录最大宽度
                    width = 0;      //宽度清零
                }
                last = rear;        //指向下一层的最右结点
            }
        }
        return max;
    }

---

后序遍历的应用

输出结点x的所有祖先（即路径）

• 设计思想：
  采用后序遍历算法，在出栈的同时判断是否为x，如果为x输出栈内所有元素。
• 算法：

void Search(BiTree bt, ElemType x) {
    BiTNode *p = bt, *r = NULL;
    InitStack(S);
    while(p || !IsEmpty(S)) {
        if(p) {     //走到最左边
            push(S, p);
            p = p->lchild;
        }else {
            getTop(S, p);
            if(p->rchild && p->rchild!=r) { //如果右结点存在且最近未被访问过
                p = p->rchild;  
            }else {
            pop(S, p);
                if(p->data == x) {
                    print(p);
                    while(!IsEmpty(S)) {
                        pop(S, p);
                        print(p);
                    }
                }
                r = p;
                p = NULL;
            }
        }
    }
}

---

最近公共祖先结点

• 设计思想：
  后序非递归，当访问到p时，将栈中所有元素复制到临时栈T，再继续访问，访问到q时，从栈顶开始比较栈S和栈T中元素，第一个相等的元素即为最近公共祖先。
• 算法：

bool Ancestor(BiTree ROOT, BiTNode *p, BiTNode *q, BiTNode *&r) {
    BiTree S[];
    int Stop = -1;
    BiTree T[];
    int Ttop = -1;
        
    BiTNode *x = ROOT, *visit = NULL;
    while(x || Stop > -1) { //IsEmpty(S)
        if(x) {         //走到最左边
            S[++Stop] = x;  //push(S, x);
            x = x->LLINK;
        }else {
            x = S[Stop];    //GetTop(S, x);
            if(x->RLINK && x->RLINK != visit) {
                x = x->RLINK;
            }else {
                x = S[Stop--];  //pop(S, x);
                if(x == p) {
                    //将栈S中的所有元素复制到临时栈T
                    for(int i=0; i<=Stop; i++) {
                        T[i] = S[i];
                        Ttop = Stop;
                    }
                }
                if(x == q) {
                    //将栈S中的所有元素从栈顶开始，分别于栈T中比较，第一个相等的元素就是最近公共祖先
                    for(int i=Stop; i>-1; i--) {
                        for(int j=Ttop; j>-1; j--) {
                            if(S[i] == T[j]) {      //相等
                                r = S[i];           //返回最近公共祖先
                                return true;        //找到了
                            }
                        }
                    }
                }
                r = x;
                x = NULL;   
            }
        }
    }
    return false;
}

---

根据遍历序列建立树

• 设计思想：
  1. 根据先序序列确定树的根结点；
  2. 根据根结点在中序序列中划分出二叉树的左右子树包含哪些结点，然后根据左右子树结点在先序序列中的次序确定子树的根结点（即回到步骤1）；
  3. 上述操作，直到每棵子树仅有一个结点（该子树的根结点）为止。
• 算法：

BiTree PreInCreat(ElemType A[], ElemType B[], int l1, int h1, int l2, int h2) {
//l1,h1为先序的第一和最后一个结点下标，l2,h2为中序的第一和最后一个结点的下标
    //初始调用时，l1=l2=1, h1=h2=n
    root = (BiTree)malloc(sizeof(BiTNode));     //建立根结点
    root->data = A[l1];         //根结点
    for(i=l2; B[i]!=root->data; i++);   //根结点在中序序列中的划分
    llen = i-12;        //左子树长度
    rlen = h2-i;        //右子树长度
    if(llen) {          //建立左子树
        root->lchild = PreInCreat(A, B, l1+1, l1+llen, l2, l2+llen-1);
    }else {
        root->lchild = NULL;
    }
    if(rlen) {          //建立右子树
        root->rchild = PreInCreat(A, B, h1-rlen+1, h1, h2-rlen+1, h2);
    }else {
        root->rchild = NULL;
    }
    return root;
}