[51nod 1681]公共祖先(dfs序+线段树合并)
题面
给出两棵n(n<=100000)个点的树,对于所有点对求它们在两棵树中公共的公共祖先数量之和。
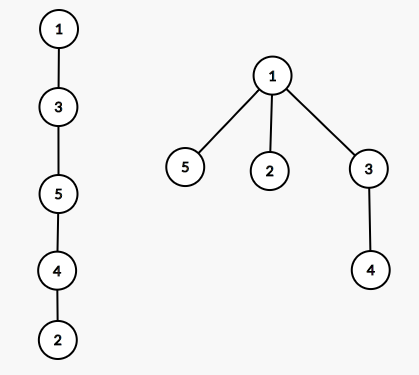
如图,对于点对(2,4),它们在第一棵树里的公共祖先为{1,3,5},在第二棵树里的公共祖先为{1},因此公共的公共祖先数量为2
把所有点对的这个数量加起来,就得到了最终答案
分析
(O(n^3))的暴力不讲了,先考虑(O(n^2))的做法
枚举点对复杂度太高,不可行。我们考虑每个节点x作为公共的公共祖先的次数。设树A上的节点x,在树B上对应的节点是x'(实际上x'和x的编号是相同的,只是这样方便描述).则如果点对既在x的子树中,对应到B上后又在x'的子树中,则这个点对的公共的公共祖先就包含x .注意一个小细节,如果x是y的父亲,x不算做x和y的祖先,所以这里的“子树”应该不包含x.

如这张图中,A中1的子树中节点有{2,3,4,5},{2,3,4,5}对应到B中均在1的子树内。这4个节点中任选一对,它们的公共祖先都包含1
那么我们只要考虑x的子树中有多少个点对应过去在树B上x'的子树中即可。暴力枚举x子树中的每个节点,然后判断。设这样的点个数为cnt,则x作为公共的公共祖先的次数就是(C_{cnt}^2),把它累加进答案
那么我们怎么把它优化呢?我们发现,节点编号是离散的,不好判断。但子树中节点的dfs序是连续的。我们把A中节点x的dfs序标记到树B上对应的位置x‘。然后我们遍历树A的每个节点x,它子树的dfs序范围为[l[x]+1,r[x]] (不包含x)。那么问题就变成在树B上编号为x的节点的子树中有多少个节点的标记落在[l[x]+1,r[x]]的范围内。
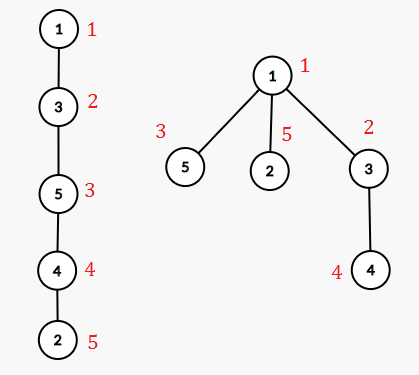
如图,我们想求A中3的子树中有多少个节点对应到B中也在3的子树里,l[3]=2,r[3]=5,B中3的子树中的dfs序有{2,4},落在[2+1,5]的范围内的只有4,所以有1个节点
这是线段树合并的经典问题。用权值线段树合并就可以了,节点x的线段树的节点[l,r] 存储有x的子树中多少个值落在[l,r]内。(有些题解用了可持久化线段树,其实没有必要)。我们遍历的时候从下往上合并,合并到节点x的时候就更新x的cnt值。
时间复杂度(O(nlog n))
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#define maxn 100000
#define maxlogn 25
using namespace std;
int n;
struct segment_tree{
#define lson(x) (tree[x].ls)
#define rson(x) (tree[x].rs)
struct node{
int ls;
int rs;
int val;
}tree[maxn*maxlogn+5];
int ptr;
void push_up(int x){
tree[x].val=tree[lson(x)].val+tree[rson(x)].val;
}
void update(int &x,int upos,int l,int r){
if(!x) x=++ptr;
if(l==r){
tree[x].val++;
return;
}
int mid=(l+r)>>1;
if(upos<=mid) update(tree[x].ls,upos,l,mid);
else update(tree[x].rs,upos,mid+1,r);
push_up(x);
}
int query(int x,int L,int R,int l,int r){
if(L<=l&&R>=r){
return tree[x].val;
}
int mid=(l+r)>>1;
int ans=0;
if(L<=mid) ans+=query(tree[x].ls,L,R,l,mid);
if(R>mid) ans+=query(tree[x].rs,L,R,mid+1,r);
return ans;
}
int merge(int x,int y,int l,int r){
if(!x||!y) return x+y;
if(l==r){
tree[x].val+=tree[y].val;
return x;
}
int mid=(l+r)>>1;
tree[x].ls=merge(tree[x].ls,tree[y].ls,l,mid);
tree[x].rs=merge(tree[x].rs,tree[y].rs,mid+1,r);
push_up(x);
return x;
}
}T;
int root[maxn+5];
int in[maxn+5];
int tim=0;
int dfnl[maxn+5],dfnr[maxn+5];
vector<int>E1[maxn+5],E2[maxn+5];
void dfs1(int x,int fa){
dfnl[x]=++tim;
for(int i=0;i<E1[x].size();i++){
int y=E1[x][i];
if(y!=fa){
dfs1(y,x);
}
}
dfnr[x]=tim;
}
int cnt[maxn+5];
void dfs2(int x,int fa){
for(int i=0;i<E2[x].size();i++){
int y=E2[x][i];
if(y!=fa){
dfs2(y,x);
root[x]=T.merge(root[x],root[y],1,n);
}
}
cnt[x]=T.query(root[x],dfnl[x]+1,dfnr[x],1,n);
}
int main(){
int u,v;
int rt1,rt2;
scanf("%d",&n);
for(int i=1;i<n;i++){
scanf("%d %d",&u,&v);
E1[u].push_back(v);
E1[v].push_back(u);
in[v]++;
}
for(int i=1;i<=n;i++) if(in[i]==0) rt1=i;//根不一定是1
memset(in,0,sizeof(in));
for(int i=1;i<n;i++){
scanf("%d %d",&u,&v);
E2[u].push_back(v);
E2[v].push_back(u);
in[v]++;
}
for(int i=1;i<=n;i++) if(in[i]==0) rt2=i;
dfs1(rt1,0);
for(int i=1;i<=n;i++){
T.update(root[i],dfnl[i],1,n);
}
dfs2(rt2,0);
long long ans=0;
for(int i=1;i<=n;i++){
ans+=(long long)cnt[i]*(cnt[i]-1)/2;
}
printf("%lld
",ans);
}