远处有一座大楼,小明想要测量大楼的高度,他想到了一个好办法:
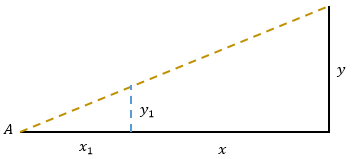
小明找到一根长度是y1的木棍插在地上,当他趴在 A点时,木棍的顶端正好遮住楼顶,此时他记录下自己的观察点到木棍的距离x1 。之后小明又找到另一个长度是y2的木棍,用同样的方法再观察一次,这次记录的数值是 x2。由于测量时存在误差,因此 x1/y1≠x2/y2,现在小明可以通过相似三角形可以建立起一个有唯一解的方程组:
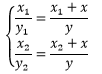
小明的两次观测数据是x1=1.061,y1=1.310,x2=1.094,y2=1.350。为了便于使用计算机计算,小明用矩阵表示方程组:
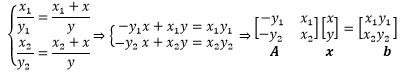
这相当于把方程组转换为Ax=b的线性形式,进而求得 x=A-1b:
1 import numpy as np 2 x1, y1 = 1.061, 1.310 3 x2, y2 = 1.094, 1.350 4 A = np.mat(np.array([[-y1, x1], [-y2, x2]])) 5 b = np.mat(np.array([x1 * y1, x2 * y2])).T 6 x = A.I * b 7 print(x)
结果是 x≈58.77,y≈73.87。
几天后,为了在同学面前炫耀,小明又去测量了一次。因为工具粗糙且视角略有差别,这次的数据是x3=1.143,y3=1.410,x4=0.922,y4=1.140 ,得到的结果是x≈94.85,y≈118.41 ,这可与之前的结果相差很大。于是小明继续测量,算上前几天的2组数据,小明一共记录了8组数据:
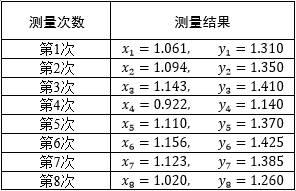
这下可坏了,任意两组数据都能得到唯一解,任意三组数据都无解!怎么办呢?
最小二乘法
常规的方法无法回答小明的问题,幸好高斯老爷子发现了最小二乘法。最小二乘法(又称最小平方法)是一种通过最小化误差的平方和,寻找数据最佳函数匹配的优化策略。
微积分视角
由于测量大楼时存在误差,所以每次计算结果都是大楼高度的近似值,这就导致8次测量的数据实际上构成了一个大型的约等方程组:
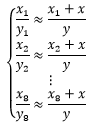
现在的问题是,约等方程组不能按照直等方程组的方法求解。对此,我们的解决思路是寻找到一组x 和y ,使得方程组中所有方程的左右两侧都尽最大可能相等。在进一步解释前,先将约等方程组转换成熟悉的线性形式:
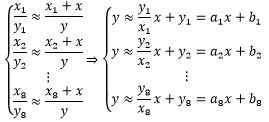
大楼就在那里,它的高度是固定不变的。既然每次测量都存在误差,那么y的真实值实际上是计算值加误差:
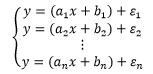
我们的目标是寻找一组合适的x 和y ,使得所有方程中的误差都尽可能小,这相当于让总体的误差最小:
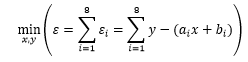
误差有正有负,将负号去掉的方式有两种,取误差的绝对值或取误差的平方,显然平方比绝对值更简单,因此先将各项取平方后再尝试找出最小值:
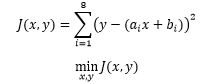
上式就是最小二乘法的公式,其中ai 和 bi是已知的,表示约等方程组中第 个方程的相关系数。如果把 J 展开,就可以直观地看出它表达的含义:
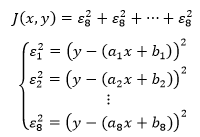
最小二乘法作为一种策略,并未指出具体的求解方案。由于极值通常出现在临界点上,所以一种可行的方案是通过寻找临界点(也就是 J 的偏导等于0的点)求解。
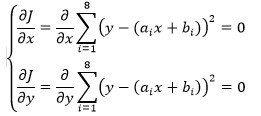
这个看上去有点吓人的求导其实很简单:
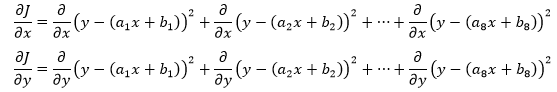
以展开式的第一项为例:
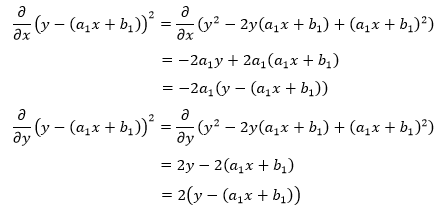
展开式的每一项都将得到类似的结果,由此我们将得到一个新的方程组:
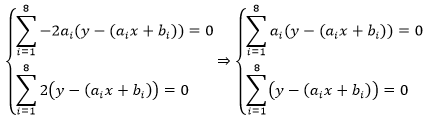
这里需要抑制住冲动,方程组中的两个方程都是和式运算,每一项的ai都不同,因此第一个方程的等式两侧不能除以 ai,即不能使用下式:
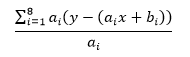
现在有两个方程,两个未知数,可以求得唯一一组解。

已经知道了ai和bi ,可以计算出方程组的解:
import numpy as np x = np.array([1.061, 1.094, 1.143, 0.922, 1.110, 1.156, 1.123, 1.020]) y = np.array([1.310, 1.350, 1.410, 1.140, 1.370, 1.425, 1.385, 1.260]) a = y / x b = y p1 = np.sum(a ** 2) p2 = np.sum(a) p3 = np.sum(a * b) q1 = p2 q2 = np.sum(b) A = np.mat(np.array([[p1, -p2], [q1, -np.alen(x)]])) b = np.mat(np.array([-p3, -q2])).T x = A.I * b print(x)
线性代数视角
从微积分的视角来看,最小二乘法相当于求解约等方程组,那么最小二乘法的线性代数视角又是什么呢?
先来看向量的投影:
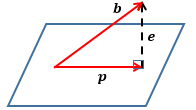
b,p,e 是3个向量,其中p是b 在平面上的投影, e是b和p 的误差向量,e=b-p 。平面可以看作二维向量张成的向量空间,p 在该空间上。将向量投影到向量空间有什么意义呢?这要从方程 Ax=b 说起。
小明根据测量结果得到了一个方程组,并将它进一步化简为矩阵的形式:
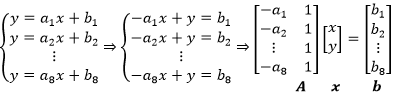
对于小明的数据来说, Ax=b无解,实际上大多数这种类型的方程都无解。 A的列空间的含义是方程组有解时b 的取值空间,当b 不在 A的列空间时,方程无解。具体来说,当A 是行数大于列数的长方矩阵时,意味着方程组中的方程数大于未知数的个数,此时肯定无解。
虽然方程无解,但我们还是希望能够运算下去,这就需要换个思路——不追求可解,转而寻找最能接近问题的解。对于无解方程Ax=b 来说,Ax 总是在列空间上(因为列空间本来就是由 Ax确定的,和b 无关),而 b就不一定了,所以需要微调 ,将p 调整至列空间中最接近它的一个,此时Ax=b 变成了:

p就是 b在 A的列空间上的投影, x上加一个小帽子表示x 的估计值。当然,因为方程无解,所以本来也不可能有 Ax=b。此时问题转换为寻找最好的估计值 ,使它尽可能满足原方程:
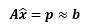
在上图中,A的秩是2,平面表示A的列空间,平面上的向量有无数个,其中最接近b 的当然是b 在平面上的投影,因为只有在这时 b-p 才能产生模最小的误差向量。
如何求得估计值呢?
在小明的测量数据中,A的列空间是一个超平面,A的两个列向量都在这个超平面上,b和p 的误差向量e垂直于超平面,因此e也垂直于超平面上的所有向量,这意味着e 和 A的两个列向量的点积为0。
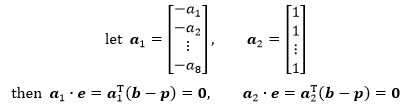
将二者归纳为一个矩阵方程:
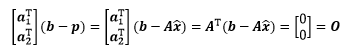
矩阵方程已经去掉了关于 的信息,通过该方程可进一步求得估计值:
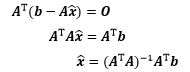
这就是最终结果了,它是由矩阵方程推导而来的,所以这个结果叫做“正规方程”。
还有一种更简单的方式可以得到正规方程。Ax=b无解的原因是因为 A 是一个长方矩阵,只要在等式两侧同时乘以 AT,就可以把长方矩阵转换成方阵,进而求解。
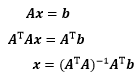
import numpy as np x = np.array([1.061, 1.094, 1.143, 0.922, 1.110, 1.156, 1.123, 1.020]) y = np.array([1.310, 1.350, 1.410, 1.140, 1.370, 1.425, 1.385, 1.260]) a1 = -(y / x) a2 = np.array([1] * 8) A = np.mat(np.array([a1, a2])).T b = np.mat(y).T x = (A.T * A).I * A.T * b print(x)
概率统计的视角
在实际应用中,我们把 J函数称为“平方差损失函数”或“平方损失函数”,通过名字自然地联想到概率统计中方差的概念。作为衡量实际问题的数字特征,方差有代表了问题的波动性,这里如何理解“波动性”呢?
大楼就在哪里,它的高度是一个真实值,假设这个值是100。接下来为了便于说明,我们把问题简单化,假设小明只需要一次测量就可以计算出大楼的高度。

表中计算结果与真实值的差就是每次计算结果与真实值的波动,把每次波动累加起来就是整体的波动,也就是问题的“波动性”。 由于每次波动都有正有负,如果直接相加的话会正负抵消,得到波动性是0的结论,这显然是荒谬的。解决这个问题的一个方法是每次波动都取绝对值,另一个方法是取波动的平方,平方不用考虑符号的问题,因此比绝对值更简单。
现在可以计算出小明8次计算的总体波动和平均波动:

相比较而言,第3次、第5次、第6次计算结果的平均波动较小,看起来似乎应该只取这3次的测量结果。问题是,小明并不知道哪些结果是波动较小的。此外,根据“大样本理论(large sample theory)”,在大样本下,只要研究数据的渐进分布即可。简单地说,只有当测量数据达到一定规模时才能得到较为正确的结果,数据越多会越好。比如乒乓球比赛偶尔会出现“爆冷”的场景,某个成绩平平的外国选手战胜了中国的顶尖选手,但你并不能因此说这名外国选手的实力更强,只能说在本次比赛中二者的波动都较大,外国选手打出了太多的“超级球”,而中国选手正好不在状态;当二者的交手逐渐增多时,他们的平均波动也将趋近于各自的真实实力,中国选手自然会找回场子。
回到原问题,从概率统计的视角来看,最小二乘法的意义是让所有样本波动之和最小化:
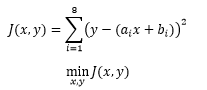
如果在平方和基础上除以测量的次数,则变成了让样本的平均波动最小:
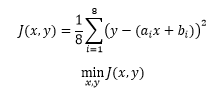
最小二乘法与线性回归
回归(Regression)是一类重要的监督学习算法,其目标是通过训练样本的学习,得到从样本特征到目标值之间的映射。在回归中,样本的标签是连续值。线性回归(Linear Regression)是回归问题中的重要一类。在线性回归中,样本特征与目标值之间是线性相关的。
回归的重要应用是预测,比如根据人的身高、性别、体重等特征预测鞋子的尺码;根据学历、专业、工作经验等特征预测薪资待遇;根据房屋的面积、楼层、户型等特征预测房屋的价格。
一元线性回归
只有一个特征的线性回归问题称为一元线性回归,其拟合曲线是一条直线,它的假设函数(hypothesis function)是:
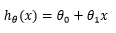
我们的目标是根据给定的训练样本找出合适的模型参数,使假设函数变成明确的模型,从而使得该模型与训练样本达到最大的拟合度。
可以使用最小二乘法作为一元线性回归的学习策略:
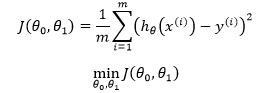
在机器学习中J称为损失函数(cost function),这里m 是训练样本的个数,y 表示样本的标签,也就是真实结果。乘以1/m 的目的是为了使损失值不至于变得过大,以便更地直观感受到模型的优劣。最小化损失函数的几何意义是所有样本到直线的函数距离最小化:
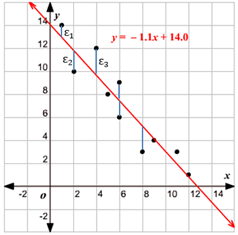
这里 x和y是已知的,而θ1和θ2才是未知的,虽然这里与小明在测量大楼时的公式有所不同,但是让整体误差到达最小的道理是一样的。推导时需要对θ1和θ2求偏导,当m=1 时:
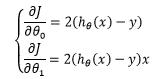
在求偏导时出现了系数2,为了约掉这个系数,通常在损失函数中除以2:
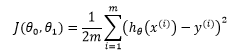
由此得到新的偏导:
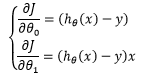
推广到 m个数据集:

令每个偏导的值都等于0,便得到了一个二元一次方程组,从而求得具体的模型参数。
多元线性回归
我们比较熟悉的概念是二维平面和三维空间,有人说四维包含了时间、五维包含了灵魂……别信他的!空间的每一个维度都可以代表任意事物,这完全取决于你对每一个维度的定义。多维空间只是个概念,不要试图在平面上通过几何的方式描述四维以及四维以上的空间。
实际上多维空间很常见,关系型数据库的表就可以看作一个多维空间,表的每个字段代表了空间的一个维度,下面就是一个十维空间的例子。

可以看到,维度的内容不仅仅包含数量,同样可以包含文字,只是为了能够计算,需要制定一些规则将文字转换成数字。
在真实的世界中,训练样本的特征可能是成千上万维,多元线性回归通过一个超平面来拟合数据。不要试图画出超平面,实际上连四维空间都没法有效地展示。画不出来没关系,能表达就好了,n维空间的超平面可以写成:
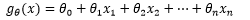
如果用向量表示:
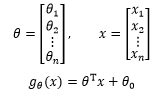
这就又变成了我们熟悉的直线方程。如果令 x0=1,可以更进一步简化 :
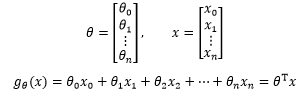
在多元线性回归中,我们依然使用最小二乘法的策略:

最终将求得:
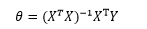
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公作者众号“我是8位的”
