第五讲 对角化与Jordan标准形
一、正规矩阵
1. 实对称矩阵与厄米矩阵
实对称矩阵:实矩阵
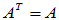
厄米矩阵:复矩阵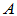
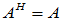
实反对称矩阵:实矩阵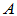

反厄米矩阵:复矩阵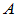
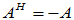
2. 正交矩阵和酉矩阵
正交矩阵:实矩阵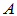
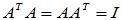 (
( )
)
酉矩阵:复矩阵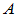
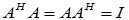 (
(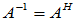 )
)
3. 正交相似变换和酉相似变换
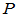 为正交矩阵,
为正交矩阵,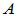 为实矩阵,
为实矩阵,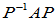 为对
为对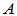 的正交相似变换;
的正交相似变换;
 为酉矩阵,
为酉矩阵,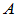 为复矩阵,
为复矩阵,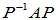 为对
为对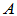 的酉相似变换。
的酉相似变换。
4. 正规矩阵
实矩阵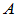 ,若满足
,若满足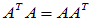 ,则
,则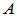 为实正规矩阵;
为实正规矩阵;
复矩阵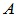 ,若满足
,若满足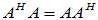 ,则
,则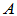 为复正规矩阵。
为复正规矩阵。
显然,实对称矩阵、实反对称矩阵、正交矩阵均为实正规矩阵;
厄米矩阵、反厄米矩阵、酉矩阵均为复正规矩阵。
5. 相似矩阵具有相同的特征多项式 相同的特征值、迹、行列式。
相同的特征值、迹、行列式。
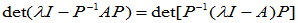
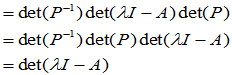 (
(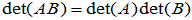 )
)
二、酉对角化
- Schur引理:设数
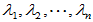 是
是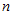 阶方阵
阶方阵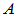 的特征值,则存在酉矩阵
的特征值,则存在酉矩阵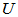 ,使
,使

[证明] 设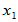 是
是 的属于特征值
的属于特征值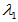 的特征向量,即
的特征向量,即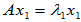 ,
,
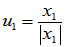 ,并由其扩充为一组标准正交向量
,并由其扩充为一组标准正交向量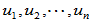

令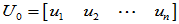 ,
,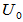 为酉矩阵
为酉矩阵
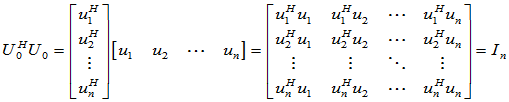
对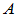 进行酉相似变换:
进行酉相似变换:
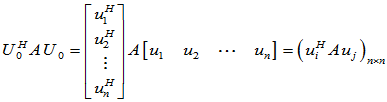
第一列: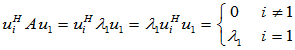


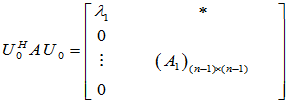
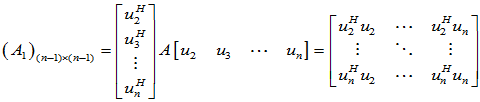
相似矩阵具有相同的特征值,因此,对于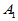 ,其特征值为
,其特征值为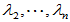 ,与上相同,可得一个酉矩阵
,与上相同,可得一个酉矩阵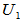 ,使得
,使得


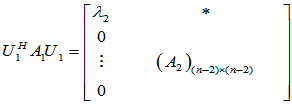
依次类推,分别可找到酉矩阵 使
使




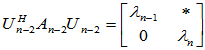
令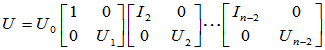

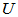 是酉矩阵,
是酉矩阵,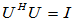
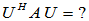

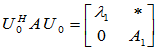
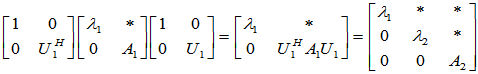

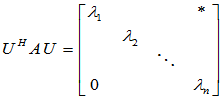
[得证]
什么样的矩阵能够通过酉相似变换成为对角阵呢?
- 定理:
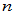 阶方阵
阶方阵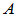 ,酉相似于对角阵的充要条件是:
,酉相似于对角阵的充要条件是: 为正规阵(实或复)。
为正规阵(实或复)。
[证明] 由Schur引理:存在酉矩阵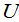 使得
使得

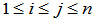
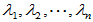 是
是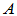 的特征值。
的特征值。
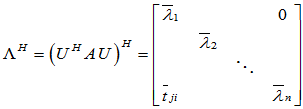
充分性:已知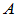 为正规阵,即
为正规阵,即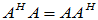 ,要证
,要证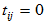
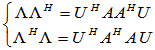
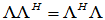
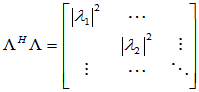

由对角元素相等可得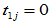 ,
,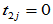 ,
,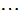 ,
,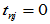
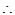
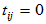
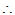
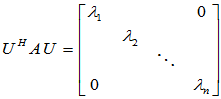
必要性:已知存在酉矩阵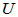 使
使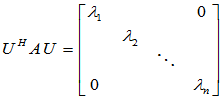
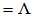 ,要证
,要证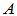 为正规矩阵。
为正规矩阵。

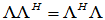
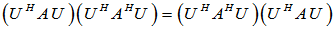
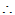
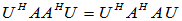
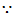
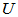 可逆
可逆
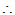

[得证]
说明:(1)不能酉对角化的矩阵仍有可能采用其它可逆变换将其对角化,例如
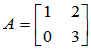
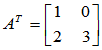

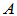 不是正规矩阵
不是正规矩阵
但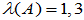 ,两个特征值互异,可以相似变换对角化。可见,
,两个特征值互异,可以相似变换对角化。可见, 可以对角化,但不能酉对角化。
可以对角化,但不能酉对角化。
(2)实正规矩阵一般不能通过正交相似变换对角化。(若特征值全为实数,则可正交相似对角化)
如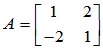 ,特征值为
,特征值为 ,
,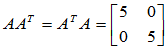 正规阵,但不可能对角化。
正规阵,但不可能对角化。
不能对角化的矩阵一定具有多重特征值,对于不能对角化的矩阵也希望找到某种标准形式,使之尽量接近对角化的形式——Jordan标准形。
三、Jordan标准形
- Jordan标准形的存在定理
任何方阵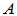 均可通过某一相似变换化为如下Jordan标准形:
均可通过某一相似变换化为如下Jordan标准形:
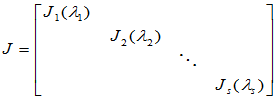
其中 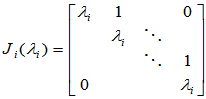 称为Jordan块矩阵。
称为Jordan块矩阵。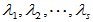 为
为 的特征值,可以是多重的。
的特征值,可以是多重的。
说明:(1)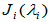 中的特征值全为
中的特征值全为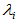 ,但是对于不同的
,但是对于不同的 、
、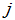 ,有可能
,有可能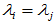 ,即多重特征值可能对应多个Jordan块矩阵。
,即多重特征值可能对应多个Jordan块矩阵。
(2)Jordan标准形是唯一的,这种唯一性是指:各Jordan块矩阵的阶数和对应的特征值是唯一的,但是各Jordan块矩阵的位置可以变化。
2. 多项式矩阵(又称为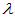 阵)
阵)
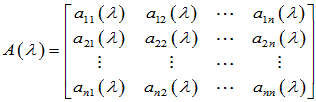
称为 的多项式矩阵,其中矩阵元素
的多项式矩阵,其中矩阵元素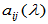 为
为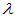 的多项式。
的多项式。
 多项式矩阵的初等变换
多项式矩阵的初等变换
初等变换的目的是为了在保持矩阵原有属性的前提下形式上变得简单。
- 互换两行(列)
- 以非零常数乘以某行(列) [这里不能乘以
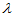 的多项式或零,这样有可能改变原来矩阵的秩和属性]
的多项式或零,这样有可能改变原来矩阵的秩和属性]
- 将某行(列)乘以
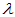 的多项式加到另一行(列)
的多项式加到另一行(列)
 多项式矩阵的标准形式:采用初等变换可将多项式矩阵化为如下形式:
多项式矩阵的标准形式:采用初等变换可将多项式矩阵化为如下形式:

其中,多项式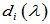 是首一多项式(首项系数为1,即最高幂次项的系数为1),且
是首一多项式(首项系数为1,即最高幂次项的系数为1),且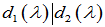 、
、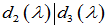 、
、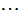 、
、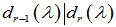 ,即
,即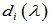 是
是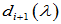 的因式。
的因式。
- 多项式矩阵的标准形式不随所采用的初等变换而变,故称
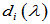 为不变因子。
为不变因子。
- 不变因子又可采用如下方法求得:设
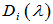 为
为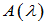 的所有
的所有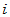 阶子行列式的最大公因式,则
阶子行列式的最大公因式,则 ,
,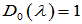 。
。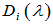 称为
称为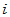 阶行列式因子。
阶行列式因子。
- 将每个不变因子化为不可约因式,这些不可约因式称为
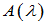 的初等因子,全体初等因子称为初等因子组。例如:
的初等因子,全体初等因子称为初等因子组。例如:

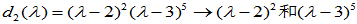
初等因子组中应包括两个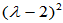 。
。
- Jordan标准形的求法
- 求出特征多项式
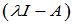 的初等因子组,设为
的初等因子组,设为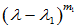 、
、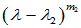 、
、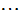 、
、 。
。
- 写出各Jordan块矩阵(一个初等因子对应一个Jordan块矩阵)
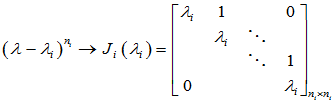
- 合成Jordan矩阵:
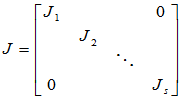
例:求矩阵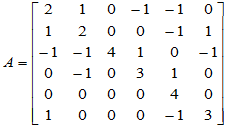 的Jordan标准形。
的Jordan标准形。
[解] 写出特征矩阵
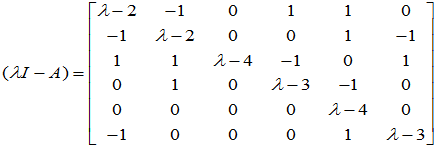
第1~4行与第1、2、4、5列交叉的元素形成的四阶子式为
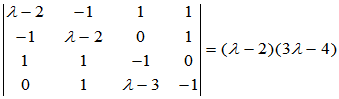
第1、2、3、5行与1、3、4、5列交叉的元素形成的四阶子式为
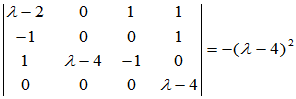
这两个子式的公因式为1,故 
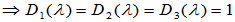
第1~5行与第1、2、3、5、6列交叉的元素形成的五阶子式为
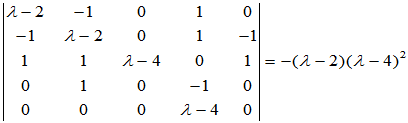
第1、2、3、5、6行与第1、3、4、5、6列交叉的元素形成的五阶子式为
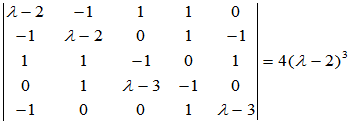
其它五阶子式均含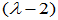 因式,故
因式,故 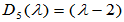
特征值行列式为 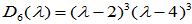 ,从而有
,从而有
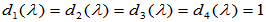 ,
, ,
,
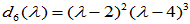
- 初等因子组为
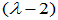 ,
,  ,
, 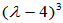
- 相应的Jordan块为
 ,
, 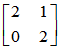 ,
, 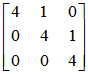
- Jordan标准形为
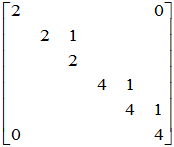
作业:P106 1(1)(2), 2, 4, 5, 10
P79 19(1)(3)
