线性基的思维题+图常见套路
Description
渐渐地,Magic Land上的人们对那座岛屿上的各种现象有了深入的了解。
为了分析一种奇特的称为梦想封印(Fantasy Seal)的特技,需要引入如下的概念:
每一位魔法的使用者都有一个“魔法脉络”,它决定了可以使用的魔法的种类。
一般地,一个“魔法脉络”可以看作一个无向图,有N个结点及M条边,将结点编号为1~N,其中有一个结点是特殊的,称为核心(Kernel),记作1号结点。每一条边有一个固有(即生成之后再也不会发生变化的)权值,是一个不超过U的自然数。
每一次魔法驱动,可看作是由核心(Kernel)出发的一条有限长的道路(Walk),可以经过一条边多次,所驱动的魔法类型由以下方式给出:
将经过的每一条边的权值异或(xor)起来,得到s。
如果s是0,则驱动失败,否则将驱动编号为s的魔法(每一个正整数编号对应了唯一一个魔法)。
需要注意的是,如果经过了一条边多次,则每一次都要计入s中。
这样,魔法脉络决定了可使用魔法的类型,当然,由于魔法与其编号之间的关系尚未得到很好的认知,此时人们仅仅关注可使用魔法的种类数。
梦想封印可以看作是对“魔法脉络”的破坏:
该特技作用的结果是,“魔法脉络”中的一些边逐次地消失。
我们记总共消失了Q条边,按顺序依次为Dis1、Dis2、……、DisQ。
给定了以上信息,你要计算的是梦想封印作用过程中的效果,这可以用Q+1个自然数来描述:
Ans0为初始时可以使用魔法的数量。
Ans1为Dis1被破坏(即边被删去)后可以使用魔法的数量。
Ans2为Dis1及Dis2均被破坏后可使用魔法的数量。
……
AnsQ为Dis1、Dis2、……、DisQ全部被破坏后可以使用魔法的数量。
Input
第一行包含三个正整数N、M、Q。
接下来的M行,每行包含3个整数,Ai、Bi、Wi,表示一条权为Wi的与结点Ai、Bi关联的无向边,其中Wi是不超过U的自然数。
接下来Q行,每行一个整数:Disi。
Output
一共包Q+1行,依次为Ans0、Ans1、……、AnsQ。
HINT
【数据规模和约定】
所有数据保证该无向图不含重边、自环。
所有数据保证不会有一条边被删除多次,即对于不同i和j,有Disi≠Disj
30%的数据中N ≤ 50,M ≤ 50,Q ≤50,U≤100;
60%的数据中N ≤ 300,M ≤ 300,Q ≤50,U≤10^9;
80%的数据中N ≤ 300,M ≤ 5000,Q ≤5000,U≤10^18;
100%的数据中N ≤ 5000,M ≤ 20000,Q ≤20000,U≤10^18;
题目分析
这里线性基图上的问题和2115Xor一样,处理的技巧是把图做成dfs树和非树边。
题目所求的问题即:在一个无向图中,求以1为起点的非简单路径的种类数。
那么和上一题一样, $所有的非简单路径$ 等价于 $一条简单路径$ + $若干个环$。而我们遇到的最主要问题在于,现在有两条路径,而它们各自和一些环异或之后,可能会存在结果相同的情况。整一个问题的瓶颈正是在于这一部分的去重。
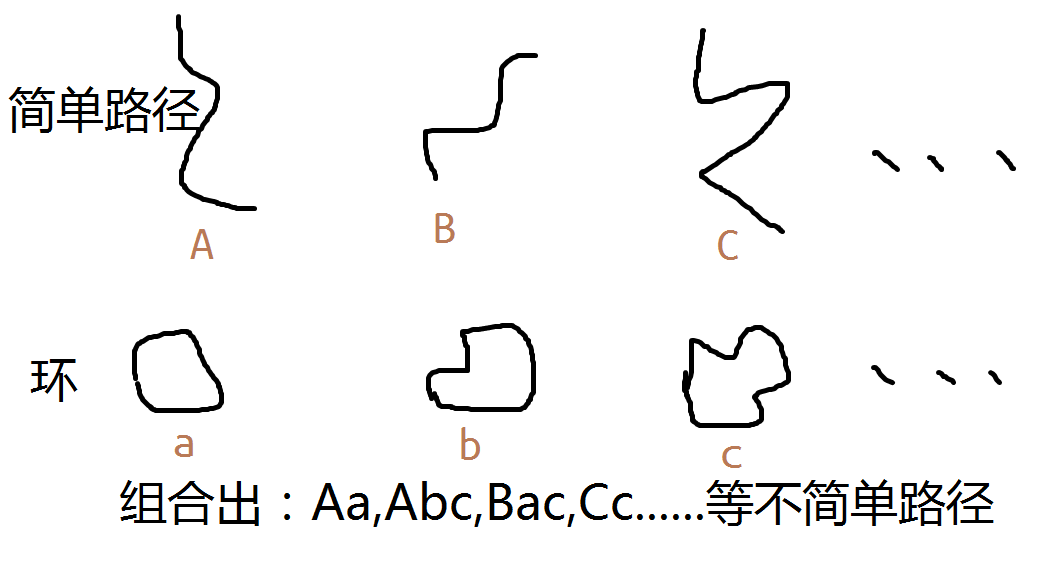
这里有一种巧妙的技巧,借鉴了最小表示的思想。
首先应该意识到,路径$A$和$B$如果存在各自异或$a$,$b$后数值相等的情况(即A xor a = B xor b),那么路径A,B实质上是等价的,因为它们的其他任何情况也必定是会相等的。
注意到线性基的性质:$(一条路径)异或(若干环)形成的值域集合$=$(一条路径先异或若干环)异或(若干环)形成的值域集合$(这里说得严谨一些就是张成相等)。那么,对于路径$A$,$B$,可以先用线性基内的环将它们“最小表示”一下,于是就保证了加进来的路径“本质不同”。
一个槽点:原数据如果不将$v[]$(存环的数组)从大到小排序,而直接按照插入顺序来“最小表示”,也能通过此题。
1 #include<bits/stdc++.h> 2 typedef long long ll; 3 const int maxn = 5035; 4 const int maxm = 40035; 5 const int maxq = 20035; 6 7 struct Edge 8 { 9 int u,v; 10 ll val; 11 Edge(int a=0, int b=0, ll c=0):u(a),v(b),val(c) {} 12 }edges[maxm],etmp[maxm]; 13 int n,m,q,del[maxq]; 14 int edgeTot,head[maxn],nxt[maxm]; 15 ll dis[maxn],p[135],ans[maxq],tmp; 16 bool tag[maxm]; 17 std::set<ll> s; 18 std::set<ll>::iterator it; 19 20 ll read() 21 { 22 char ch = getchar(); 23 ll num = 0, fl = 1; 24 for (; !isdigit(ch); ch = getchar()) 25 if (ch=='-') fl = -1; 26 for (; isdigit(ch); ch = getchar()) 27 num = (num<<1)+(num<<3)+ch-48; 28 return num*fl; 29 } 30 void addedge(int u, int v, ll c) 31 { 32 edges[++edgeTot] = Edge(u, v, c), nxt[edgeTot] = head[u], head[u] = edgeTot; 33 edges[++edgeTot] = Edge(v, u, c), nxt[edgeTot] = head[v], head[v] = edgeTot; 34 } 35 ll calc(ll c) 36 { 37 for (int i=1; i<=p[0]; i++) 38 if ((c^p[i]) < c) c ^= p[i]; 39 return c; 40 } 41 void update(ll c) 42 { 43 if (!c) return; 44 for (it=s.begin(); it!=s.end(); it=s.upper_bound(tmp)) 45 { 46 tmp = *it; 47 if ((tmp^c) < tmp) 48 s.erase(it), s.insert(tmp^c); 49 } 50 p[++p[0]] = c; 51 for (int j=p[0]; j>=2; j--) 52 if (p[j] > p[j-1]) std::swap(p[j], p[j-1]); 53 else break; 54 } 55 void dfs(int x, int fa, ll c) 56 { 57 dis[x] = c, tmp = calc(c); 58 if (tmp&&(s.count(tmp)==0)) s.insert(tmp); 59 for (int i=head[x]; i!=-1; i=nxt[i]) 60 { 61 int v = edges[i].v; 62 if (v!=fa){ 63 if (dis[v]==-1) dfs(v, x, c^edges[i].val); 64 else update(calc(dis[v]^c^edges[i].val)); 65 } 66 } 67 } 68 void connect(int u, int v, ll c) 69 { 70 addedge(u, v, c); 71 if (dis[u]!=-1&&dis[v]!=-1) update(calc(dis[u]^dis[v]^c)); 72 else{ 73 if (dis[u]==-1&&dis[v]==-1) return; 74 if (dis[u]==-1) dfs(u, v, dis[v]^c); 75 else dfs(v, u, dis[u]^c); 76 } 77 } 78 int main() 79 { 80 memset(dis, -1, sizeof dis); 81 memset(head, -1, sizeof head); 82 n = read(), m = read(), q = read(), dis[1] = 0, s.insert(0); 83 for (int i=1; i<=m; i++) 84 etmp[i].u = read(), etmp[i].v = read(), etmp[i].val = read(); 85 for (int i=1; i<=q; i++) del[i] = read(), tag[del[i]] = 1; 86 for (int i=1; i<=m; i++) 87 if (!tag[i]) connect(etmp[i].u, etmp[i].v, etmp[i].val); 88 ans[q+1] = s.size()*(1ll<<p[0])-1; 89 for (int i=q; i; i--) 90 { 91 connect(etmp[del[i]].u, etmp[del[i]].v, etmp[del[i]].val); 92 ans[i] = s.size()*(1ll<<p[0])-1; 93 } 94 for (int i=1; i<=q+1; i++) printf("%lld ",ans[i]); 95 return 0; 96 } 97 /* 98 8 10 0 99 8 4 5 100 4 5 9 101 7 1 5 102 1 4 9 103 2 8 1 104 6 5 5 105 8 3 6 106 7 4 7 107 7 3 6 108 1 3 3 109 */
END