一、主成分分析是利用降维的方法,在损失很少信息量很少的前提下,把多个指标转换为几个综合指标的多元统计方法。通常把转化的综合指标称为主成分。
二、基本原理
在对某一事物进行研究时,为了更全面、准确地反应事物的特征及其发展规律人们通常考虑一起有关系的多个指标,也叫变量。
三、主成分分析步骤
1、根据问题选取初始变量
2、根据初始变量特性判断由协方差矩阵求主成分还是由相关阵求主成分
3、求协方差矩阵或相关矩阵的特征根和相应的标准特征向量
4、判断是否存在明显的多重共线性,若存在则回到第一步。
5、得到主成分的表达式并确定主成分个数,选取主成分
6、结合主成分对研究问题进行深入的分析
四、主成分上机实现
1、princomp函数为主成分分析的主要函数
其用法为princomp(formula,data=NULL,subset,na.action.....)
其中formula是没有响应变量的公式,data是数据框,或者
princomp(x,cor=FALSE,scores=TURE,covmat=NULL,subset=rep(TURE,nrow(as.matrix(x))),....)
其中x是主要分析的数据,以数值矩阵或数据框的形式给出,cor为逻辑变量,当cor为TURE表示用样本的协方差阵做主成分分析,反之用协方差阵,covmat是协方差阵,如果数据不由x提供就是由其提供。
2、summary函数提取出相应的信息
summary(object,loadings=FALSE,cutoff=0,1...)
objict表示princom()得到的对象,loadings为TRUE时,表示显示loadings的内容,反之显示。
3、loadings()显示主成分分析或因子分析中的内容
4、predict()
predict(objict)用来预测主成分的值。
5、screeplot()函数用于画碎石图,使用格式为screeplot(x,npcs=min(10,length(x$sdev)),type=c("barplot","lines"))
npcs是主成分的个数,type描述其类型,分别为直方图和直线图的类型。
6、biplot()函数主要画出主成分的散点图和原坐标在主成分下的方向,使用格式为
biplot(x,choice=1:2,scale=1,pc.boplot=FALSE....)
choice是选择主成分,默认为1,2主成分,bc.plot为逻辑变量默认为FALSE。
7、实例
下表是某工业部门13个行业,分别是冶金(1)、电力(2)、煤炭、化学、机械、建材、森工、食品、纺织、缝纫、皮革、造纸、和文化教育艺术品,8个指标分别为
年末固定资产净产值(x1,万元)、职工人数、工业总产值、全员劳动生产率、百元固定原值实现产值、资金利润率(x6)、标准燃料消费量和能源利用效果。
(1)试用主成分分析方法确定8个指标的几个主成分,并对其进行解释
(2)利用主成分得分对13个行业进行排序和分类。
X1 X2 X3 X4 X5 X6 X7 X8 1 90342 52455 101091 19272 82.0 16.1 197435 0.172 2 4903 1973 2035 10313 34.2 7.1 592077 0.003 3 6735 21139 3767 1780 36.1 8.2 726396 0.003 4 49454 36241 81557 22504 98.1 25.9 348226 0.985 5 139190 203505 215898 10609 93.2 12.6 139572 0.628 6 12215 16219 10351 6382 62.5 8.7 145818 0.066 7 2372 6572 8103 12329 184.4 22.2 20921 0.152 8 11062 23078 54935 23804 370.4 41.0 65486 0.263 9 17111 23907 52108 21796 221.5 21.5 63806 0.276 10 1206 3930 6126 15586 330.4 29.5 1840 0.437 11 2150 5704 6200 10870 184.2 12.0 8913 0.274 12 5251 6155 10383 16875 146.4 27.5 78796 0.151 13 14341 13203 19396 14691 94.6 17.8 6354 1.574
1 1 w=read.csv("afh.csv") 2 2 w 3 3 attach(w) 4 4 X1 5 5 #### 作主成分分析 6 6 w.pr<-princomp(w, cor=TRUE)#利用协方差作主成分分析 7 7 w.pr 8 8 #### 并显示分析结果
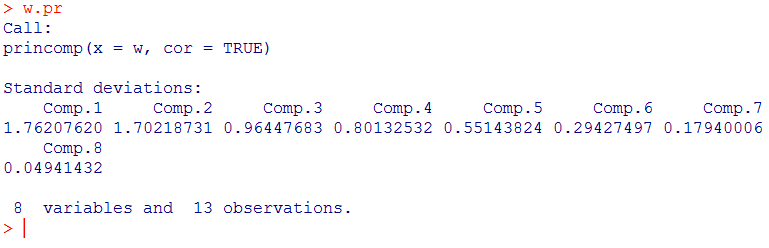
Standard devi....其中可以看出其标准差,即主成分的方差开方,也就是相应特征值lambda1、lambda2、lambda3到lambda8的特征值的开方
1 summary(w.pr, loadings=TRUE) 2 3 #### 作预测 4 predict(w.pr) 5 6 #### 画碎石图 7 screeplot(w.pr) 8 screeplot(w.pr,type="lines",pch=25,col=4) 9 10 biplot(w.pr) 11 12 princomp(~X1+X2+X3+X4+X5+X6+X7+X8,data=w, cor=T)

在这里我们也同样可以看出一些关键的信息。
其中Standard devi....其中可以看出其标准差,即主成分的方差开方,也就是相应特征值lambda1、lambda2、lambda3到lambda8的特征值的开方。
proportion of Var....表示方差的贡献率。
Cumulative proportion表示方差的累积贡献率
Loadings=TURE表示列出载荷的内容,即有8个主成分,因此可以根据方差累积贡献率大于85%可以选取主成分,以达到降维的目的。在这可以选取comp.1、comp.2、comp.2



第一主成分和第二主成分的散点图

预测值:

(2)综合得分:以个主成分的贡献率为权,将其线性组合得到综合评价函数:
C=(lambda1*C1+lambda2*C2+….+lambdaiCi)/(lambda1+lambda2+….+lambdai)
在这我们选取的是第一第二主成分,这其主成分得分为:w8
A<-c(1.7620762 ,1.7021873,0.96447683 )####默认为列
B<-sqrt(A)
B[1]
B[2]
B[3]
X1<-w.pr$scores[,1]
X1
X2<-w.pr$scores[,2]
X3<-w.pr$scores[,3]
X3
w2<-data.frame(X1,X2,X3)
w4<-matrix(X1,nrow=13)
w4
w41<-matrix(X2,nrow=13)
w41
w42<-matrix(X3,nrow=13)
w42
w5<-w4%*%B[1]/(B[1]+B[2]+B[3])
w5
w6<-w41%*%B[2]/(B[1]+B[2]+B[3])
w6
w7<-w42%*%B[3]/(B[1]+B[2]+B[3])
w7
w8=w5+w6+w7
w8
rank(w8)
或者这样也可以调用mvstats包运用princomp.rank(m=3,w.pr)函数就可以
princomp.rank(m=3,w.pr)
(2)分类:
w=scale(w)####数据标准化
d=dist(w)####聚类距离
d
plot(h1,hang=-1,main=c("聚类分析"),sub=c("最短距离或者最近邻法"))###使用labels=iris$Species[iris]加下标
hh1=rect.hclust(h1,k=3,border=c(2:3))###将h1分类加颜色
######表示最短距离或者最近邻法
二、主成分回归
在回归分析中,曾经讲过,当自变量出现多重共线性时,经典回归方法作回归系数的最小二乘法估计一般效果会比较差,而采取主成分回归能够客服直接回归的不足,下面用例子进行说明。
对某地区某类消费品的销售量y进行调查,它与下面四个变量有关,居民可支配收入(x1)、该类消费品平均价格指数(x2)、社会该消费品保有量(x3)、其他消费品平均价格指数(x4)。
用主成分回归方法建立营销量y与其他变量的关系。
数据如下:
x1=c(82.9,88.0,99.9,105.3,117.7,131.0,148.2,161.8,174.2,184.7)
x2=c(92.0,93.0,96.0,94.0,100,101,105,112,112,112)
x3=c(17.1,21.3,25.1,29.0,34,40,44,49,51,53)
x4=c(94,96,97,99,100,101,104,109,111,111)
y1=c(8.4,9.6,10.4,11.4,12.2,14.2,15.8,17.9,29.6,20.8)
用R编写程序可得:
1 x1=c(82.9,88.0,99.9,105.3,117.7,131.0,148.2,161.8,174.2,184.7) 2 x2=c(92.0,93.0,96.0,94.0,100,101,105,112,112,112) 3 x3=c(17.1,21.3,25.1,29.0,34,40,44,49,51,53) 4 x4=c(94,96,97,99,100,101,104,109,111,111) 5 y1=c(8.4,9.6,10.4,11.4,12.2,14.2,15.8,17.9,29.6,20.8) 6 length(x3) 7 w=data.frame(x1,x2,x3,x4,y1) 8 lm.sol<-lm(y1~x1+x2+x3+x4) 9 summary(lm.sol)
运行结果如下:

在这可以看出,按4个变量得到的回归方程为
y=-114.8655+0.02438x1-0.215x2-0.233x3+1.53x4
cor(w)
可以得到:相关系数矩阵

仔细分析得到的结果,可以看出计算出来的回归系数并不显著,可能存在多重共线性。
因此,用主成分回归进行分析,其代码如下:
1 conomy<-princomp(~x1+x2+x3+x4,cor=T)####主成分分析 2 summary(conomy,loadings=T)
得到结果如下:
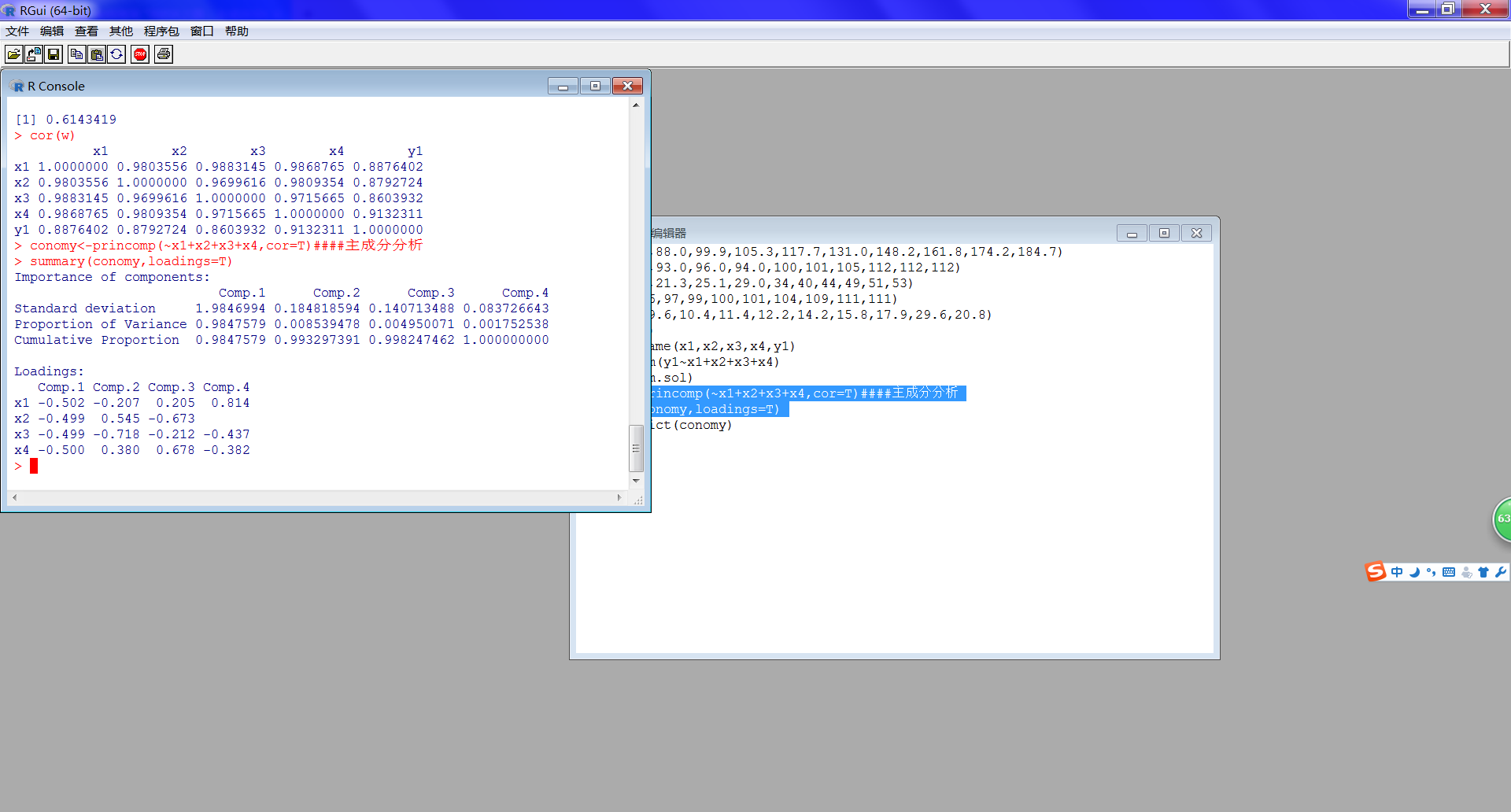
首先我们可以看出前两个主成分的贡献率以达到99%,在这我们可以看到第一主成分是关于居民可支配收入(x1)、该类消费品平均价格指数(x2)、社会该消费品保有量(x3)、其他消费品平均价格指数(x4)。在这我们可以看到第二主成分也是如此。
但是我们将两个主成分带入原公式,这是不符合经济意义的,所以我们的多重共线性并未消。
下面作主成分回归
首先计算主成分的预测值,并且将第一主成分和第二主成分的预测值放入数据框中,然后做主成分回归。
pre<-predict(conomy)
pre
w$z1<-pre[,1]
w$z2<-pre[,2]
lm.sol2<-lm(y1~z1+z2,data=w)
summary(lm.sol2)

可以得到回归方程为:y1=15.03-2.738z1+4.4458z2
这样看不出与变量之间的关系于是我们变换一下表达式
ba<-coef(lm.sol2)###提取回归系数
ba[2]
A<-loadings(conomy)
x.bar<-conomy$center####s数据中心,均值
x.sd<-conomy$scale###标准差
coef<-(ba[2]*A[,1]+ba[3]*A[,2])/x.sd###x1x2x3x4的系数
coef
ba0<-ba[1]-sum(x.bar*coef)###常数
ba0

即回归方程为:y1= -641.2539+0.01315832x1+0.49188577x2 -0.14875597 x3+ 0.51413117x4
可见这样较为合理。