【题目描述】
给定一个(n)个节点的树,每个节点表示一个整数,问(u)到(v)的路径上有多少个不同的整数。
【输入格式】
第一行有两个整数(n)和(m)((n=40000,m=100000))。
第二行有(n)个整数。第(i)个整数表示第(i)个节点表示的整数。
在接下来的(n-1)行中,每行包含两个整数(u,v),描述一条边((u,v))。
在接下来的(m)行中,每一行包含两个整数(u,v),询问(u)到(v)的路径上有多少个不同的整数。
【输出格式】
对于每个询问,输出结果。
题解
树上莫队的模板题
原先莫队是在线性结构上进行的,现在我们要把它挪到树上
很容易想到要用dfs序之类的东西来处理
但是这里dfs序并不方便处理 因为树上一条路径上的点的dfs序不是连续一段的
我们考虑一下这棵树的欧拉序
dfs序是节点第一次被经过的时间戳,也就是每个点第一次进入搜索栈的时间戳
而欧拉序则是每个节点出栈时还要被算一次(也就是dfs回溯时再算一次)
举个例子
盗一张洛谷题解的图
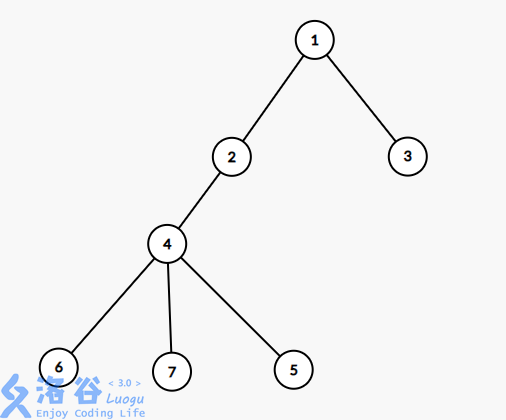
这棵树 dfs序可以是1,2,4,6,7,5,3
则欧拉序是1,2,4,6,6,7,7,5,5,4,2,3,3,1
我们把一个点入栈的时间戳记为(dfn[x]),出栈时间戳记为(out[x])(个人习惯,当然也有人是用(st[x])和(ed[x]))
现在树上的一条路径能不能被表示成一段连续区间了呢?
假设询问的是(x,y)间的路径
第一种情况 (x)是(y)的直接祖先
(反过来也一样,直接把(x,y)交换一下)
假设问的是(2 ightarrow 7)的路径吧 我们看一下(dfn[2]sim dfn[7])之间的欧拉序是什么样的:
是2,4,6,6,7
但是(6)并不在(2 ightarrow 7)的路径里
注意到只有(6)出现了两次 出现了两次就说明先加上了它的贡献 然后又删掉了 所以有贡献的实际上只有(2,4,7)
实现的时候可以记录一下当前区间里某个数(i)有没有出现 如果出现了就删掉 反之就加上
第二种情况 (x)不是(y)的直接祖先
假设是(7 ightarrow 3),看一下(out[7]sim dfn[3])之间的欧拉序:
7,5,5,4,2,3
(5)出现了两次 所以实际上没产生贡献
但是路径上应该还有一个节点(1)啊
这里我们需要判断一下 如果是第二种情况,即(x,y)的最近公共祖先不是(x) 那么统计答案是要额外加上lca的贡献
到此就和普通莫队没有差别了 分块大小取(sqrt{n})(其实严格来说是(sqrt{2n}),不过差别不大)
p.s. 怎么保证一定是(x)是(y)的祖先 而不是(y)是(x)的祖先?如果(dfn[x]>dfn[y])那么(swap(x,y))即可
代码
#include <bits/stdc++.h>
#define N 200005
using namespace std;
inline int read() {
int x = 0, f = 1; char ch = getchar();
for (; ch > '9' || ch < '0'; ch = getchar()) if (ch == '-') f = -1;
for (; ch <= '9' && ch >= '0'; ch = getchar()) x = (x << 3) + (x << 1) + (ch ^ '0');
return x * f;
}
inline void write(int x) {
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
int n, m, a[N], srt[N], block;
int head[N], pre[N<<1], to[N<<1], sz;
int ans[N], nowl, nowr, nowans, cnt[N];
bool vis[N];
inline void addedge(int u, int v) {
pre[++sz] = head[u]; head[u] = sz; to[sz] = v;
pre[++sz] = head[v]; head[v] = sz; to[sz] = u;
}
int fa[N], son[N], rnk[N], top[N], dfn[N], out[N], tme, siz[N], d[N];
void dfs(int x) {
siz[x] = 1; dfn[x] = ++tme; rnk[tme] = x;
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa[x]) continue;
d[y] = d[x] + 1;
fa[y] = x;
dfs(y);
siz[x] += siz[y];
if (!son[x] || siz[son[x]] < siz[y]) son[x] = y;
}
out[x] = ++tme; rnk[tme] = x;
}
void dfs2(int x, int tp) {
top[x] = tp;
if (son[x]) dfs2(son[x], tp);
for (int i = head[x]; i; i = pre[i]) {
int y = to[i];
if (y == fa[x] || y == son[x]) continue;
dfs2(y, y);
}
}
inline int LCA(int x, int y) {
while (top[x] != top[y]) {
if (d[top[x]] < d[top[y]]) swap(x, y);
x = fa[top[x]];
}
if (d[x] > d[y]) swap(x, y);
return x;
}
struct query{
int l, r, lca, id;
inline friend bool operator < (query x, query y) {
if (x.l / block != y.l / block) return x.l < y.l;
else return x.r < y.r;
}
} q[N];
inline void del(int c) {
if (--cnt[c] == 0) nowans--;
}
inline void add(int c) {
if (++cnt[c] == 1) nowans++;
}
inline void calc(int x) {
if (vis[x]) {
del(a[x]);
vis[x] = 0;
} else {
add(a[x]);
vis[x] = 1;
}
}
int main() {
n = read(), m = read();
block = sqrt(n);
for (int i = 1; i <= n; i++) a[i] = srt[i] = read();
sort(srt + 1, srt + n + 1);
int mx = unique(srt + 1, srt + n + 1) - srt - 1;
for (int i = 1; i <= n; i++) a[i] = lower_bound(srt + 1, srt + mx + 1, a[i]) - srt;
for (int i = 1, u, v; i < n; i++) {
u = read(), v = read();
addedge(u, v);
}
dfs(1); dfs2(1, 1);
for (int i = 1, u, v; i <= m; i++) {
u = read(), v = read();
if (dfn[u] > dfn[v]) swap(u, v);
int lca = LCA(u, v);
if (lca == u) {
q[i] = {dfn[u], dfn[v], 0, i};
} else {
q[i] = {out[u], dfn[v], lca, i};
}
}
sort(q + 1, q + m + 1);
nowl = 1, nowr = 0;
for (int i = 1; i <= m; i++) {
while (nowl < q[i].l) calc(rnk[nowl++]);
while (nowl > q[i].l) calc(rnk[--nowl]);
while (nowr < q[i].r) calc(rnk[++nowr]);
while (nowr > q[i].r) calc(rnk[nowr--]);
if (q[i].lca) calc(q[i].lca);
ans[q[i].id] = nowans;
if (q[i].lca) calc(q[i].lca);
}
for (int i = 1; i <= m; i++) {
write(ans[i]);
puts("");
}
return 0;
}