有一类关于区间最大值和最小值之类的问题,利用单调性,可以采用分治算法解决。
SPOJ22343 Norma
题意,给定一个数列,定义区间的代价为区间最大值、区间最小值、区间长度的乘积,求所有区间的代价和。
既然是分治,我们肯定要处理一个数列跨过中点的答案。
假设当前数列的中点为mid,我们从mid往前扫,扫到了i。
然后根据单调性,我们越往左扫,最大值单调不降,最小值单调不增。
那么我们可以在右边维护一个指针,表示满足最大值的区间的最靠右的端点。
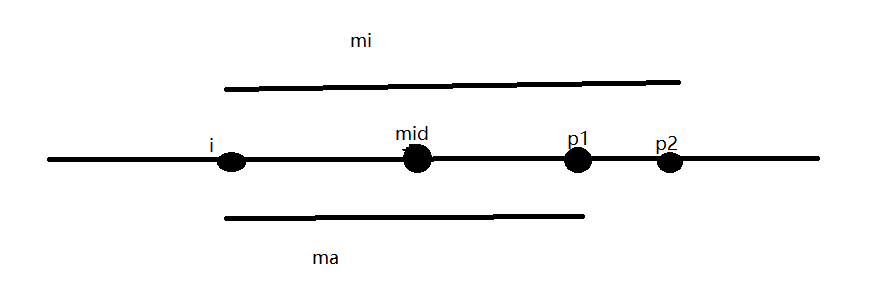
假设有这么一种情况,那么我们可以把区间拆成mid~p1,p1~p2,p2~r,三段。
1、mid~p1,max和min都是已知的,max*min*(r-l+1)。
2、p1~p2,min是已知的,我们需要算一个sigma(max)再乘上区间长度搞个前缀和算一下。
3、maxmin都未知,我们还需要维护max*min*区间长度搞成前缀和。
Code
#include<iostream> #include<cstdio> #define N 500010 #define inf 1e18 using namespace std; typedef long long ll; const int mod=1e9; ll ans,a[N],mn[N][2],mi[N][2],ji[N][2]; int n; inline ll calc(ll l,ll r){ return ((l+r)*(r-l+1)/2)%mod; } void solve(int l,int r){ if(l==r){(ans+=a[l]*a[l]%mod)%=mod;return;} ll mid=(l+r)>>1; solve(l,mid);solve(mid+1,r); ll maxn=-inf,minn=inf; mn[mid][0]=mn[mid][1]=mi[mid][0]=mi[mid][1]=ji[mid][0]=ji[mid][1]=0; for(ll i=mid+1;i<=r;++i){ maxn=max(maxn,a[i]);minn=min(minn,a[i]); mn[i][0]=(mn[i-1][0]+maxn)%mod;mn[i][1]=(mn[i-1][1]+maxn*(i-mid)%mod)%mod; mi[i][0]=(mi[i-1][0]+minn)%mod;mi[i][1]=(mi[i-1][1]+minn*(i-mid)%mod)%mod; ji[i][0]=(ji[i-1][0]+minn*maxn%mod)%mod;ji[i][1]=(ji[i-1][1]+minn*maxn%mod*(i-mid)%mod)%mod; } ll p=mid+1,q=mid+1;maxn=-inf;minn=inf; for(ll i=mid;i>=l;--i){ minn=min(minn,a[i]);maxn=max(maxn,a[i]); while(p<=r&&a[p]>=minn)p++; while(q<=r&&a[q]<=maxn)q++; int ls=min(p,q),rs=max(p,q); (ans+=maxn*minn%mod*calc(mid+1-i+1,ls-i)%mod)%=mod; if(p<q)ans=(ans+((mi[rs-1][0]-mi[ls-1][0])*(mid-i+1)%mod+mi[rs-1][1]-mi[ls-1][1])%mod*maxn%mod+mod)%mod; if(p>q)ans=(ans+((mn[rs-1][0]-mn[ls-1][0])*(mid-i+1)%mod+mn[rs-1][1]-mn[ls-1][1])%mod*minn%mod+mod)%mod; ans=((ans+(ji[r][0]-ji[rs-1][0])*(mid-i+1)%mod+(ji[r][1]-ji[rs-1][1])%mod)%mod+mod)%mod; } } int main(){ scanf("%d",&n); for(int i=1;i<=n;++i)scanf("%lld",&a[i]); solve(1,n); cout<<ans; return 0; }
CF526F
化简题意,给定一个排列,求有多少区间满足max-min=r-l;
和上题一样,考虑跨过中点的答案,因为我们要计算合法区间,所以这和max和min的分布情况有关。
最大值最小值都在一侧的情况,max,min,l都已知,r是可以O(1)求出的,直接判断就好了。
如果最大值最小值分布在两侧,我们可以在一边枚举最端点,在右边用双指针维护一个区间满足最大值在左边,最小值在右边。
然后max-min=r-l -> max+l=r+min用桶维护这个式子。
最大值最小值在右边,最小值在左边最大值在右边的情况同理。
Code
#include<iostream> #include<cstdio> #define N 300002 #define inf 0x3f3f3f3f using namespace std; int ma[N],mi[N],a[N],l,r,tong[N<<1],n; long long ans; void solve(int l,int r){ if(l==r){ans++;return;} int mid=(l+r)>>1; solve(l,mid);solve(mid+1,r); ma[mid]=0;mi[mid]=inf; for(int i=mid+1;i<=r;++i){ ma[i]=max(ma[i-1],a[i]); mi[i]=min(mi[i-1],a[i]); } ma[mid]=mi[mid]=a[mid]; for(int i=mid-1;i>=l;--i){ ma[i]=max(ma[i+1],a[i]); mi[i]=min(mi[i+1],a[i]); } int p=mid+1,q; for(int i=mid;i>=l;--i){ p=ma[i]-mi[i]+i; if(p<=r&&p>=mid+1&&ma[p]<ma[i]&&mi[p]>mi[i])ans++; } p=mid; for(int i=mid+1;i<=r;++i){ p=i-ma[i]+mi[i]; if(p>=l&&p<=mid&&ma[p]<ma[i]&&mi[p]>mi[i])ans++; } p=q=mid; for(int i=mid+1;i<=r;++i){ while(ma[p]<ma[i]&&p>=l)tong[mi[p]-p+n]++,p--; while(mi[q]>mi[i]&&q>p)tong[mi[q]-q+n]--,q--; ans+=tong[ma[i]-i+n]; } while(q>p)tong[mi[q]-q+n]--,q--; p=q=mid+1; for(int i=mid;i>=l;--i){ while(ma[p]<ma[i]&&p<=r)tong[mi[p]+p]++,p++; while(mi[q]>mi[i]&&q<p)tong[mi[q]+q]--,q++; ans+=tong[ma[i]+i]; } while(q<p)tong[mi[q]+q]--,q++; } int main(){ scanf("%d",&n); for(int i=1;i<=n;++i){ scanf("%d%d",&l,&r); a[l]=r; } solve(1,n); cout<<ans; return 0; }