我们知道感知器算法对于不能完全线性分割的数据是无能为力的,在这一篇将会介绍另一种非常有效的二分类模型——逻辑回归。在分类任务中,它被广泛使用
逻辑回归是一个分类模型,在实现之前我们先介绍几个概念:
几率(odds ratio):
其中p表示样本为正例的概率,当然是我们来定义正例是什么,比如我们要预测某种疾病的发生概率,那么我们将患病的样本记为正例,不患病的样本记为负例。为了解释清楚逻辑回归的原理,我们先介绍几个概念。
我们定义对数几率函数(logit function)为:
对数几率函数的自变量p取值范围为0-1,通过函数将其转化到整个实数范围中,我们使用它来定义一个特征值和对数几率之间的线性关系为:
在这里,p(y=1|x)是某个样本属于类别1的条件概率。我们关心的是某个样本属于某个类别的概率,刚好是对数几率函数的反函数,我们称这个反函数为逻辑函数(logistics function),有时简写为sigmoid函数:
其中z是权重向量w和输入向量x的线性组合:
现在我们画出这个函数图像:
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls='dotted')
plt.yticks([0.0, 0.5, 1.0])
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$phi (z)$')
plt.show()
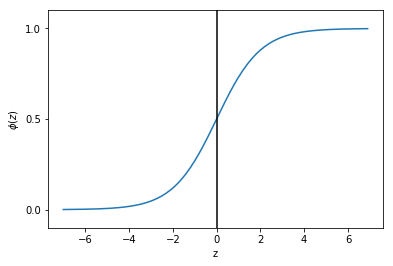
可以看出当z接近于正无穷大时,函数值接近1,同样当z接近于负无穷大时,函数值接近0。所以我们知道sigmoid函数将一个实数输入转化为一个范围为0-1的一个输出。
我们将逻辑函数将我们之前学过的Adaline联系起来,在Adaline中,我们的激活函数的函数值与输入值相同,而在逻辑函数中,激活函数为sigmoid函数。
sigmoid函数的输出被解释为某个样本属于类别1的概率,用公式表示为:
也就是当函数值大于0.5时,表示某个样本属于类别1的概率大于0.5,于是我们就将此样本预测为类别1,否则为类别0。我们仔细观察上面的sigmoid函数图像,上式也等价于:
逻辑回归的受欢迎之处就在于它可以预测发生某件事的概率,而不是预测这件事情是否发生。
我们已经介绍了逻辑回归如何预测类别概率,接下来我们来看看逻辑回归如何更新权重参数w。
对于Adaline,我们的损失函数为:
我们通过最小化这个损失函数来更新权重w。为了解释我们如何得到逻辑回归的损失函数,在构建逻辑回归模型时我们要最大化似然L(假设数据集中的所有样本都是互相独立的):
通常我们会最大化L的log形式,我们称之为对数似然函数:
这样做有两个好处,一是当似然很小时,取对数减小了数字下溢的可能性,二是取对数后将乘法转化为了加法,可以更容易的得到函数的导数。现在我们可以使用一个梯度下降法来最大化对数似然函数,我们将上面的对数似然函数转化为求最小值的损失函数J:
为了更清晰的理解上式,我们假设对一个样本计算它的损失函数:
可以看出,当y=0时,式子的第一部分为0,当y=1时,式子的第二部分为0,也就是:
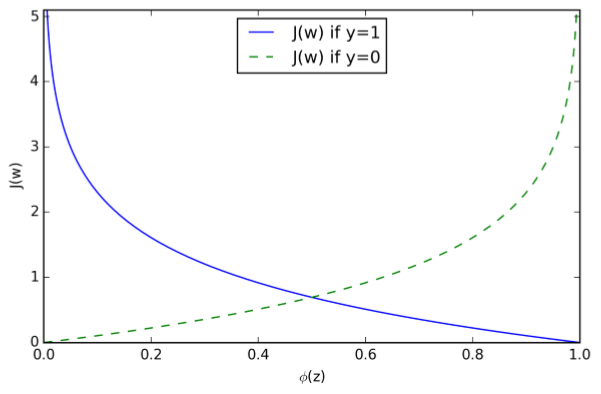
可以看出,当我们预测样本所属于的类别时,当预测类别是样本真实类别的概率越大时,损失越接近0,而当预测类别是真实类别的概率越小时,损失越接近无穷大。
作为举例,我们这里对权重向量w中的一个分量进行更新,首先我们求此分量的偏导数:
在继续下去之前,我们先计算一下sigmoid函数的偏导数:
现在我们继续:
所以我们的更新规则为:
因为我们要同时更新权重向量w的所有分量,所以我们更新规则为(此处w为向量):
因为最大化对数似然函数也就等价于最小化损失函数J,于是梯度下降更新规则为: