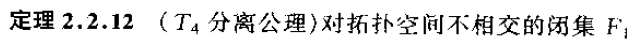参考:
文献3:拓扑空间——高国士
一、写在前面
现代数学是我目前觉得最美的数学。数学三大分支:代数,几何,分析学。最终毫无例外地用集合论解释了,真是神奇,让人拍案叫绝。以前总是思考,所有的数学到底归根于什么?当时学代数,学函数,觉得所有数学就是集合、映射。没想到真有有点不谋而合的感觉。但是没想过分析学用集合论也能解释得毫无破绽。至于几何学,当然学解释几何时,能感觉到有点解方程,用代数解决的感觉。但也没想过用齐次坐标表达,最终任意的几何形式,也能用简洁的式子描述。简言之,集合论让人惊叹不已。
如果没有问数学最底层的理论基础,那么,很多东西变得可笑,如图,你可能证明命题,证来证去都是一个,而自己都不知道,甚至也不知道哪个定理先有,哪个后有的,而把后有的定理证明先有的定理。数学家们致力于把把所有的数学定理建成一套完备的定理,并最终依赖简单的几条公理。看过公理的,你就会发笑,这么简单的东西,还有人去证啊?是的,从最简单的公理出发,树状地推导所有的定理,最终建立一套完备的定理系统。

二、简单回顾一下现代数学第一、二章:
1、集合交、并;基、势,映射、可列集、连续集;等价关系、序关系;实数的完备性定理(有限开覆盖定理,公理或许更合适一些,这里用几百个等价命题),其中一个就是极限的定义。
2、二元运算;群、环、模、线性空间;线性算子、线性泛函、张量空间
三、拓扑空间
至此,假设上述知识已经掌握。现在写一下,自己对第三章的拓扑空间的理解。是学习的过程,很可能有许多错误的理解,但是研究不怕出错。
高国士先生的书有400页来解释拓扑空间。我只能略略地叹息。
1、讲拓扑空间,先说用什么用!(工科的心态啊!)。拓扑空间用来自然地从集合概念引入极限的概念,进而为分析学打下基础。另外,拓扑空间可以在等价关系中推导、而不必在序关系中提出极限概念?(待思考)。实际很多概念是忽略这两种关系提出的。
2、先蛮不讲理地提出一些概念:拓扑空间、拓扑基、开集、闭集、邻域、邻域基、Hausdorff space、内点、外点、边界点、孤立点、极限点(累积点)、稠密、有界集、全有界集、列紧集、紧集、收敛、连续映射、同胚映射、连通、度量空间、度量空间的连通性(部分概念只是描述过程中的产物,避免重复写一堆文字才创造出的概念,并无需对它有深刻的理解。这些概念如同代码中的函数,就是避免重复写那段重复代码才创造函数)
3、拓扑空间定义:给定一个集合X,这个集合有许多子集,我们把部分或全部子集收集起来,并要求它们满足一些约束条件,由此组成的空间称为拓扑空间(X,ζ).满足的约束条件是:任意子集的叫仍在是收集中的某个子集;任意多个子集的并仍是收集中的某个子集。收集中一定有空集和X。
4、拓扑基:在收集的子集中,找到至少数量的子集,通过这些子集本身及一些数量子集之间的并可以创造出收集中的任何一个子集
5、开集、闭集:收集中的任何一个子集都是开集。以X为全集,开集的补集叫做闭集。那么,这里的开集、闭集和以前的开区间、闭区间有没有关系呢?我们也类比一些,假如,开区间类比开集,闭区间类比闭集,什么类比集合X?令某个区间是X,拓扑空间可能无数个X的子区间的组成的族,闭区间就是X-这个开区间。我们引用文献2中的一个解释:
Closed set(闭集合)。在现代的拓扑学的公理化体系中,开集和闭集是最基本的概念。一切从此引申。这两个概念是开区间和闭区间的推广,它们的根本地位,并不是一 开始就被认识到的。经过相当长的时间,人们才认识到:开集的概念是连续性的基础,而闭集对极限运算封闭——而极限正是分析的根基。
很明显,这不能说明离散拓扑的意义?在我看来,闭区间和开区间是特殊的闭集和开集。我们看下图。线段代表X(无论开集或闭集),中间中括号代表开集,两侧代表闭集。我们发现两侧也属于X,也算开集。这提示我们,这里举的例子很特殊,及开区间、闭区间也是特殊的开集、闭集。我们下面可以看出这点。

6、还是先提一下:平凡拓扑(最粗)、离散拓扑(最细):所有子集构成、通常拓扑:数直线上的开集族连通空间及R形成R上的通常拓扑。摘:在离散拓扑空间中,任何子集都是闭集,也同时是闭集,任何子集的闭包就是自己。平凡空间非空子集的闭包都是X。P22
7、设X的子集U包含着某个开集,该开集包含着x,称U为x的邻域;如果U是开集,则称U是x的开邻域。
8、Hausdorff space空间。(T2空间)
因为一般的拓扑空间研究比较单一、抽象,我们会逐渐给出一些约束条件。
首先:T0空间。

其次:T1空间。

接着:T2空间。



再者,T3:

最后,T4: