写在前面:
1.Wasserstein GAN(下面简称WGAN)成功地做到了以下爆炸性的几点:
- 彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判别器的训练程度
- 基本解决了collapse mode的问题,确保了生成样本的多样性
- 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程,这个数值越小代表GAN训练得越好,代表生成器产生的图像质量越高(如题图所示)
- 以上一切好处不需要精心设计的网络架构,最简单的多层全连接网络就可以做到
2.WGAN只改了四点:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行
第一部分:原始GAN究竟出了什么问题?
原始GAN中判别器要最小化如下损失函数,尽可能把真实样本分为正例,生成样本分为负例:
(公式1 )
其中是真实样本分布,
是由生成器产生的样本分布。对于生成器,Goodfellow一开始提出来一个损失函数,后来又提出了一个改进的损失函数,分别是
(公式2)
(公式3)
后者在WGAN两篇论文中称为“the - log D alternative”或“the - log D trick”。WGAN前作分别分析了这两种形式的原始GAN各自的问题所在,下面分别说明。
第一种原始GAN形式的问题
一句话概括:判别器越好,生成器梯度消失越严重。WGAN前作从两个角度进行了论证,第一个角度是从生成器的等价损失函数切入的。
首先从公式1可以得到,在生成器G固定参数时最优的判别器D应该是什么。对于一个具体的样本,它可能来自真实分布也可能来自生成分布,它对公式1损失函数的贡献是
令其关于的导数为0,得
化简得最优判别器为:
(公式4)
这个结果从直观上很容易理解,就是看一个样本来自真实分布和生成分布的可能性的相对比例。如果
且
,最优判别器就应该非常自信地给出概率0;如果
,说明该样本是真是假的可能性刚好一半一半,此时最优判别器也应该给出概率0.5。
然而GAN训练有一个trick,就是别把判别器训练得太好,否则在实验中生成器会完全学不动(loss降不下去),为了探究背后的原因,我们就可以看看在极端情况——判别器最优时,生成器的损失函数变成什么。给公式2加上一个不依赖于生成器的项,使之变成
注意,最小化这个损失函数等价于最小化公式2,而且它刚好和判别器损失函数相反。将最优判别器即公式4代入,再进行简单的变换可以得到
(公式5)
变换成这个样子是为了引入Kullback–Leibler divergence(简称KL散度)和Jensen-Shannon divergence(简称JS散度)这两个重要的相似度衡量指标,后面的主角之一Wasserstein距离,就是要来吊打它们两个的。所以接下来介绍这两个重要的配角——KL散度和JS散度:
(公式6)
(公式7)
于是公式5就可以继续写成
(公式8)
到这里读者可以先喘一口气,看看目前得到了什么结论:根据原始GAN定义的判别器loss,我们可以得到最优判别器的形式;而在最优判别器的下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布与生成分布
之间的JS散度。我们越训练判别器,它就越接近最优,最小化生成器的loss也就会越近似于最小化
和
之间的JS散度。
问题就出在这个JS散度上。我们会希望如果两个分布之间越接近它们的JS散度越小,我们通过优化JS散度就能将“拉向”
,最终以假乱真。这个希望在两个分布有所重叠的时候是成立的,但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略(下面解释什么叫可忽略),它们的JS散度是多少呢?
答案是,因为对于任意一个x只有四种可能:
且
且
且
且
第一种对计算JS散度无贡献,第二种情况由于重叠部分可忽略所以贡献也为0,第三种情况对公式7右边第一个项的贡献是,第四种情况与之类似,所以最终
。
换句话说,无论跟
是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS散度就固定是常数
,而这对于梯度下降方法意味着——梯度为0!此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的;即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题。
但是与
不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。
我们就得到了WGAN前作中关于生成器梯度消失的第一个论证:在(近似)最优判别器下,最小化生成器的loss等价于最小化与
之间的JS散度,而由于
与
几乎不重叠或者重叠部分可忽略,所以无论它们相距多远JS散度都是常数
,最终导致生成器的梯度(近似)为0,梯度消失。
有了这些理论分析,原始GAN不稳定的原因就彻底清楚了:判别器训练得太好,生成器梯度消失,生成器loss降不下去;判别器训练得不好,生成器梯度不准,四处乱跑。只有判别器训练得不好不坏才行,但是这个火候又很难把握,甚至在同一轮训练的前后不同阶段这个火候都可能不一样,所以GAN才那么难训练。
第二种原始GAN形式的问题
一句话概括:最小化第二种生成器loss函数,会等价于最小化一个不合理的距离衡量,导致两个问题,一是梯度不稳定,二是collapse mode即多样性不足。WGAN前作又是从两个角度进行了论证,下面只说第一个角度,因为对于第二个角度我难以找到一个直观的解释方式,感兴趣的读者还是去看论文吧(逃)。
如前文所说,Ian Goodfellow提出的“- log D trick”是把生成器loss改成
(公式3)
上文推导已经得到在最优判别器下
(公式9)
我们可以把KL散度(注意下面是先g后r)变换成含的形式:
(公式10)
由公式3,9,10可得最小化目标的等价变形
注意上式最后两项不依赖于生成器G,最终得到最小化公式3等价于最小化
(公式11)
这个等价最小化目标存在两个严重的问题。第一是它同时要最小化生成分布与真实分布的KL散度,却又要最大化两者的JS散度,一个要拉近,一个却要推远!这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个JS散度项的毛病。
第二,即便是前面那个正常的KL散度项也有毛病。因为KL散度不是一个对称的衡量,与
是有差别的。以前者为例
- 当
而
时,
,对
贡献趋近0
- 当
而
时,
,对
贡献趋近正无穷
换言之,对于上面两种错误的惩罚是不一样的,第一种错误对应的是“生成器没能生成真实的样本”,惩罚微小;第二种错误对应的是“生成器生成了不真实的样本” ,惩罚巨大。第一种错误对应的是缺乏多样性,第二种错误对应的是缺乏准确性。这一放一打之下,生成器宁可多生成一些重复但是很“安全”的样本,也不愿意去生成多样性的样本,因为那样一不小心就会产生第二种错误,得不偿失。这种现象就是大家常说的collapse mode。
第一部分小结:在原始GAN的(近似)最优判别器下,第一种生成器loss面临梯度消失问题,第二种生成器loss面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚不平衡导致mode collapse这几个问题。
第二部分:Wasserstein距离的优越性质
原始GAN问题的根源可以归结为两点,一是等价优化的距离衡量(KL散度、JS散度)不合理,二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。
Wasserstein距离又叫Earth-Mover(EM)距离,定义如下:
(公式12)
解释如下:是
和
组合起来的所有可能的联合分布的集合,反过来说,
中每一个分布的边缘分布都是
和
。对于每一个可能的联合分布
而言,可以从中采样
得到一个真实样本
和一个生成样本
,并算出这对样本的距离
,所以可以计算该联合分布
下样本对距离的期望值
。在所有可能的联合分布中能够对这个期望值取到的下界
,就定义为Wasserstein距离。
直观上可以把理解为在
这个“路径规划”下把
这堆“沙土”挪到
“位置”所需的“消耗”,而
就是“最优路径规划”下的“最小消耗”,所以才叫Earth-Mover(推土机)距离。
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近。WGAN本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布和
,
在线段AB上均匀分布,
在线段CD上均匀分布,通过控制参数
可以控制着两个分布的距离远近。
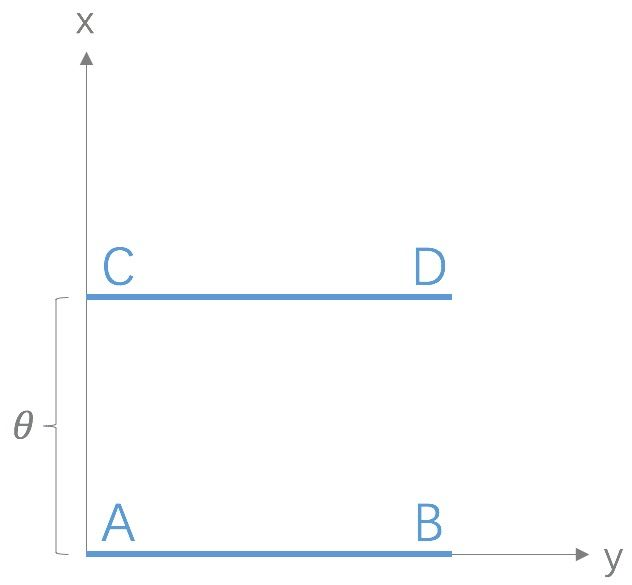
此时容易得到(读者可自行验证)
(突变)
(突变)
(平滑)
KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,如果我们要用梯度下降法优化这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
第四部分:从Wasserstein距离到WGAN
既然Wasserstein距离有如此优越的性质,如果我们能够把它定义为生成器的loss,不就可以产生有意义的梯度来更新生成器,使得生成分布被拉向真实分布吗?
没那么简单,因为Wasserstein距离定义(公式12)中的没法直接求解,不过没关系,作者用了一个已有的定理把它变换为如下形式
(公式13)
证明过程被作者丢到论文附录中了,我们也姑且不管,先看看上式究竟说了什么。
首先需要介绍一个概念——Lipschitz连续。它其实就是在一个连续函数上面额外施加了一个限制,要求存在一个常数
使得定义域内的任意两个元素
和
都满足
此时称函数的Lipschitz常数为
。
简单理解,比如说的定义域是实数集合,那上面的要求就等价于
的导函数绝对值不超过
。再比如说
就不是Lipschitz连续,因为它的导函数没有上界。Lipschitz连续条件限制了一个连续函数的最大局部变动幅度。
公式13的意思就是在要求函数的Lipschitz常数
不超过
的条件下,对所有可能满足条件的
取到
的上界,然后再除以
。特别地,我们可以用一组参数
来定义一系列可能的函数
,此时求解公式13可以近似变成求解如下形式
(公式14)
再用上我们搞深度学习的人最熟悉的那一套,不就可以把用一个带参数
的神经网络来表示嘛!由于神经网络的拟合能力足够强大,我们有理由相信,这样定义出来的一系列
虽然无法囊括所有可能,但是也足以高度近似公式13要求的那个
了。
最后,还不能忘了满足公式14中这个限制。我们其实不关心具体的K是多少,只要它不是正无穷就行,因为它只是会使得梯度变大
倍,并不会影响梯度的方向。所以作者采取了一个非常简单的做法,就是限制神经网络
的所有参数
的不超过某个范围
,比如
,此时关于输入样本
的导数
也不会超过某个范围,所以一定存在某个不知道的常数
使得
的局部变动幅度不会超过它,Lipschitz连续条件得以满足。具体在算法实现中,只需要每次更新完
后把它clip回这个范围就可以了。
到此为止,我们可以构造一个含参数、最后一层不是非线性激活层的判别器网络
,在限制
不超过某个范围的条件下,使得
(公式15)
尽可能取到最大,此时就会近似真实分布与生成分布之间的Wasserstein距离(忽略常数倍数
)。注意原始GAN的判别器做的是真假二分类任务,所以最后一层是sigmoid,但是现在WGAN中的判别器
做的是近似拟合Wasserstein距离,属于回归任务,所以要把最后一层的sigmoid拿掉。
接下来生成器要近似地最小化Wasserstein距离,可以最小化,由于Wasserstein距离的优良性质,我们不需要担心生成器梯度消失的问题。再考虑到
的第一项与生成器无关,就得到了WGAN的两个loss。
(公式16,WGAN生成器loss函数)
(公式17,WGAN判别器loss函数)
公式15是公式17的反,可以指示训练进程,其数值越小,表示真实分布与生成分布的Wasserstein距离越小,GAN训练得越好。