【网络流】最大权闭合图

目录

简介
原理
代码

简介

首先说一下什么是闭合图，在图中选取某些点构成点集记为 (V) ，如果集合中的出边所指向的终点也在 (V) 中，则称 (V) 为闭合图。（注意到这个“闭合图”其实是一个点集）

而最大权闭合图，顾名思义，就是对于一个图中的所有闭合图构成的集合中，点权和最大的元素。

给出一个图，如何求它的最大权闭合图呢？我们借助网络流的最小割解决这个问题。

原理

先说说如何建图：
原图 (G=(V,E)) ，流网络 (N=(V_N, E_N)) ，(V_N=V+{s,t}) ，(E_N={(s,u),w_u>0}cup{(u,t),w_u<0}cup E)

流网络的容量：原图中的边容量为 (∞) ，源点向正权点连边容量即为点权，负权点向汇点连边容量为点权的相反数。（自然，点权为 (0) 的点是不需要讨论的）

比如原图：

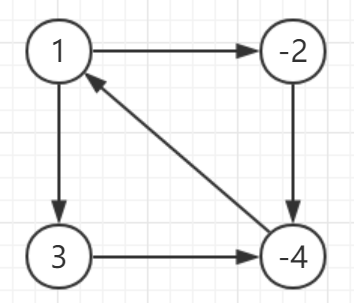
流网络：

[-----------split~line -----------]

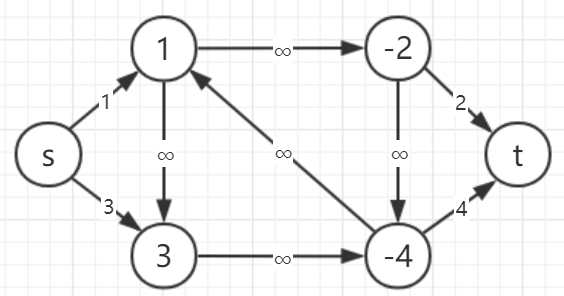
简单割：
针对于最大权闭合图这个问题，我们给出简单割的定义：对于流网络的一个割，如果割边一定是与源点或者汇点相连的，那么称这个割为简单割。

自然，最小割一定是简单割，因为如果某个割割边取到原图中对应的边时，对应的容量一定为 (∞) ，显然不可能是最小割。

下证：闭合图与简单割一一对应

约定 (overline{V'}=V-V')

• 闭合图对应简单割
  对于一个闭合图 (V') ，进行构造：(S=V'+{s}) ， (T=V_N-S)
  根据闭合图的定义，可以发现不存在边是从 (V') 到 (overline{V'}) 的，所以割 ([S,T]) 一定是简单割。

• 简单割对应闭合图
  对于一个简单割 ([S,T]) ，构造： (V'=S-{s}) ，由简单割的定义，不存在边从 (V') 到 (overline{V'}) ，因此 (V'=S-{s}) 是闭合图。

然后，我们考察简单割的容量与闭合图点权和的关系：

注意到简单割的容量由且只由 (V' ightarrow t) 以及 (s ightarrow overline{V'}) 构成，正式的说，有：

[c[S,T] = c[V',{t}] + c[{s},overline{V'}] ]

约定 (V^+) 为 (V) 中的正权点集，负权点集为 (V^-)

那么上式可以进一步化为：

[c[S,T] = sum_{u in V'^-}(-w_u) + sum_{u in overline{V'}^+}(w_u) ]

而 (V') 点权和可以写成：

[sum w(V') = sum_{u in V'^+}(w_u)-sum_{u in V'^-}(-w_u) ]

将上述两式相加，即得：

[sum w(V') + c[S,T] = sum_{u in V'^+}(w_u)+sum_{u in overline{V'}^+}(w_u) ]

右式为 (V) 的正点权和，为常数，所以当 (c[S,T]) 为最小割时，(sum w(V')) 最大。

至此，问题解决。

模板题传送门：https://www.acwing.com/problem/content/963/

代码

#include<bits/stdc++.h>
using namespace std;

const int N=55050, M=50005*3+N<<1, INF=0x3f3f3f3f;

int n, m, S, T;

struct node{
    int to, next, c;    
}e[M];

int h[N], tot;

void add(int u, int v, int c){
    e[tot].to=v, e[tot].c=c, e[tot].next=h[u], h[u]=tot++;
    e[tot].to=u, e[tot].c=0, e[tot].next=h[v], h[v]=tot++;
}

int q[N], d[N], cur[N];
bool bfs(){
    memset(d, -1, sizeof d);
    int tt=-1, hh=0;
    q[++tt]=S, d[S]=0, cur[S]=h[S];

    while(tt>=hh){
        int hd=q[hh++];
        for(int i=h[hd]; ~i; i=e[i].next){
            int go=e[i].to;
            if(d[go]==-1 && e[i].c){
                d[go]=d[hd]+1;
                cur[go]=h[go];
                if(go==T) return true;
                q[++tt]=go;
            }
        }
    }
    return false;
}

int find(int u, int limit){
    if(u==T) return limit;
    int flow=0;
    for(int i=cur[u]; ~i && limit>flow; i=e[i].next){
        int go=e[i].to;
        cur[u]=i;
        if(d[go]==d[u]+1 && e[i].c){
            int t=find(go, min(e[i].c, limit-flow));
            if(!t) d[go]=-1;
            e[i].c-=t, e[i^1].c+=t, flow+=t;
        }
    }
    return flow;
}

int dinic(){
    int res=0, flow;
    while(bfs()) while(flow=find(S, INF)) res+=flow;
    return res;
}

int main(){
    memset(h, -1, sizeof h);
    cin>>n>>m;

    S=0, T=n+m+1;
    for(int i=1; i<=n; i++){
        int w; cin>>w;
        add(m+i, T, w);
    }

    int cnt=0;
    for(int i=1; i<=m; i++){
        int v1, v2, w; cin>>v1>>v2>>w;
        cnt+=w;
        add(i, m+v1, INF), add(i, m+v2, INF);
        add(S, i, w);
    }

    cout<<cnt-dinic()<<endl;

    return 0;
}