题意
计数 (1 sim n) 的排列,满足 (p_i in (i - n +a, i - a))。
(a le 10^5, n le 10^9)
题解
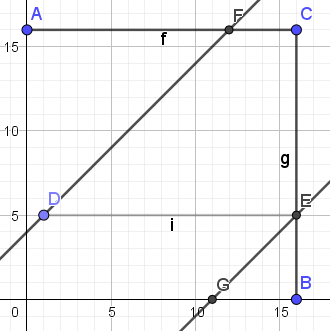
为了便于描述,将限制画在图上,横轴表示 (i),纵轴表示 (p_i)。
把图转来转去看几遍,发现一种比较可做的方式是先考虑 (FCED) 里的点,每行必须有一个,从上往下,每行都只有 (a) 种选择,方案数 (a!)。
还剩下 (a) 列没有被使用,对应 (p_i in [1, a])。
这时唯一限制就是 ( riangle FGB) 中的点不能选,那么容斥一下,就是强行钦定 (i) 列必须选在 ( riangle FGB) 中,那么 (FCED) 中每次可选的方案数就仅剩 (a - i) 种了。
DP 这样钦定的方案数。设考虑了 (p) 列,已经选了 (q) 个点,(f(p, q) = f(p -1, q) + (p-q+1)f(p - 1, q - 1))。
最后答案是
[sum_{i=0}^{a} (-1)^{a-i} (a - i)!(a-i)^{n-a}f(a, i)
]
可以发现第二维翻转((q o p + 1 - q)),这样就是第二类 Stirling 数,那么写个 NTT 就好。
#include <cstdio>
#include <algorithm>
using namespace std;
const int M = 998244353;
inline int add(int x, int y) {return x+y>=M ? x+y-M : x+y;}
template<class ...Args> inline int add(int x, int y, Args... args) {return add(add(x, y), args...);}
inline int sub(int x, int y) {return x-y<0 ? x-y+M : x-y;}
inline int mul(int x, int y) {return 1LL * x * y % M;}
template<class ...Args> inline int mul(int x, int y, Args... args) {return mul(mul(x, y), args...);}
inline void inc(int &x, int y=1) {x += y; if(x >= M) x -= M;}
inline void dec(int &x, int y=1) {x -= y; if(x < 0) x += M;}
inline int power(int x, int y){
int res = 1;
for(; y; y>>=1, x = mul(x, x)) if(y & 1) res = mul(res, x);
return res;
}
inline int inv(int x){return power(x, M - 2);}
const int N = 262144;
int W[N], invW[N], rev[N], last = 0;
void init(){
W[0] = invW[0] = 1;
W[1] = power(3, (M - 1) / N); invW[1] = inv(W[1]);
for(int i=2; i<N/2; i++){
W[i] = mul(W[i - 1], W[1]);
invW[i] = mul(invW[i - 1], invW[1]);
}
}
void make_rev(int n){
if(n == last) return;
int l = __builtin_ctz(n) - 1;
last = n;
for(int i=1; i<n; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << l);
}
void dft(int a[], int n, int w[] = W){
make_rev(n);
for(int i=1; i<n; i++)
if(i < rev[i]) swap(a[i], a[rev[i]]);
for(int l=2, k=1; k<n; l<<=1, k<<=1){
const int step = N / l;
for(int i=0; i!=n; i+=l)
for(int j=i, e=0, li=i+k; j!=li; j++, e+=step){
int x = a[j], y = mul(a[j | k], w[e]);
a[j] = add(x, y);
a[j | k] = sub(x, y);
}
}
}
void idft(int a[], int n, int pres){
dft(a, n, invW);
int iN = inv(n);
for(int i=0; i<pres; i++) a[i] = mul(a[i], iN);
fill(a + pres, a + n, 0);
}
void idft(int a[], int n){
dft(a, n, invW);
int iN = inv(n);
for(int i=0; i<n; i++) a[i] = mul(a[i], iN);
}
void Dot(int a[], const int b[], const int n){
for(int i=0; i<n; i++) a[i] = mul(a[i], b[i]);
}
int len(int n){
int l = 1;
while(l < n) l <<= 1;
return l;
}
int fac[N], ifac[N], s2[N], g[N];
void pre_stirling(int n){
fac[0] = 1;
for(int i=1; i<=n; i++) fac[i] = mul(fac[i - 1], i);
ifac[n] = inv(fac[n]);
for(int i=n-1; i>=0; i--) ifac[i] = mul(ifac[i + 1], i + 1);
for(int i=0; i<=n; i++){
s2[i] = mul(power(i, n), ifac[i]);
if(i & 1) g[i] = M - ifac[i];
else g[i] = ifac[i];
}
int l = len(n * 2 + 1);
init();
dft(s2, l); dft(g, l); Dot(s2, g, l); idft(s2, l);
}
int main(){
int n, a;
scanf("%d%d", &n, &a);
if(a >= n){
puts("0");
return 0;
}
pre_stirling(a + 1);
int res = 0;
for(int i=0; i<=a; i++)
if(i & 1) dec(res, mul(power(a - i, n - a), fac[a - i], s2[a + 1 - i]));
else inc(res, mul(power(a - i, n - a), fac[a - i], s2[a + 1 - i]));
printf("%d
", res);
return 0;
}