差分约束2
参考:
夜深人静写算法(四) - 差分约束 - 英雄哪里出来 - C++博客
http://www.cppblog.com/menjitianya/archive/2015/11/19/212292.html
一、引例
1、一类不等式组的解
给定n个变量和m个不等式,每个不等式形如 x[i] - x[j] <= a[k] (0 <= i, j < n, 0 <= k < m, a[k]已知),求 x[n-1] - x[0] 的最大值。例如当n = 4,m = 5,不等式组如图一-1-1所示的情况,求x3 - x0的最大值。

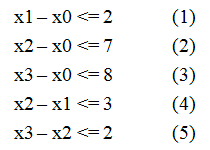
图一-1-1
1. (3) x3 - x0 <= 8
2. (2) + (5) x3 - x0 <= 9
3. (1) + (4) + (5) x3 - x0 <= 7
这里的T等于{8, 9, 7},所以min{ T } = 7,答案就是7。的确是7吗?我们再仔细看看,发现的确没有其它情况了。那么问题就是这种方法即使做出来了还是带有问号的,不能确定正确与否,如何系统地解决这类问题呢?
让我们来看另一个问题,这个问题描述相对简单,给定四个小岛以及小岛之间的有向距离,问从第0个岛到第3个岛的最短距离。如图一-1-2所示,箭头指向的线段代表两个小岛之间的有向边,蓝色数字代表距离权值。
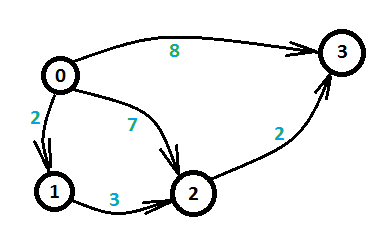


图一-1-2
这个问题就是经典的最短路问题。由于这个图比较简单,我们可以枚举所有的路线,发现总共三条路线,如下:
1. 0 -> 3 长度为8
2. 0 -> 2 -> 3 长度为7+2 = 9
3. 0 -> 1 -> 2 -> 3 长度为2 + 3 + 2 = 7
最短路为三条线路中的长度的最小值即7,所以最短路的长度就是7。这和上面的不等式有什么关系呢?最短路求解其实是和上面一样的。
二、差分约束
1、数形结合
介绍完最短路,回到之前提到的那个不等式组的问题上来,我们将它更加系统化。
如若一个系统由n个变量和m个不等式组成,并且这m个不等式对应的系数矩阵中每一行有且仅有一个1和-1,其它的都为0,这样的系统称为差分约束( difference constraints )系统。引例中的不等式组可以表示成如图三-1-1的系数矩阵。

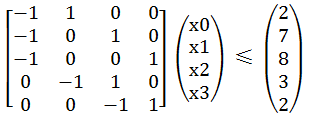
图三-1-1
然后继续回到单个不等式上来,观察 x[i] - x[j] <= a[k], 将这个不等式稍稍变形,将x[j]移到不等式右边,则有x[i] <= x[j] + a[k],然后我们令a[k] = w(j, i),再将不等式中的i和j变量替换掉,i = v, j = u,将x数组的名字改成d(以上都是等价变换,不会改变原有不等式的性质),则原先的不等式变成了以下形式:d[u] + w(u, v) >= d[v]。
这时候联想到SPFA中的一个松弛操作:
if(d[u] + w(u, v) < d[v]) {
d[v] = d[u] + w(u, v);
}
d[v] = d[u] + w(u, v);
}
对比上面的不等式,两个不等式的不等号正好相反,但是再仔细一想,其实它们的逻辑是一致的,因为SPFA的松弛操作是在满足小于的情况下进行松弛,力求达到d[u] + w(u, v) >= d[v],而我们之前令a[k] = w(j, i),所以我们可以将每个不等式转化成图上的有向边:
对于每个不等式 x[i] - x[j] <= a[k],对结点 j 和 i 建立一条 j -> i的有向边,边权为a[k],求x[n-1] - x[0] 的最大值就是求 0 到n-1的最短路。

图三-1-2
2、三角不等式
如果还没有完全理解,我们可以先来看一个简单的情况,如下三个不等式:
B - A <= c (1)
C - B <= a (2)
C - A <= b (3)
我们想要知道C - A的最大值,通过(1) + (2),可以得到 C - A <= a + c,所以这个问题其实就是求min{b, a+c}。将上面的三个不等式按照 三-1 数形结合 中提到的方式建图,如图三-2-1所示。

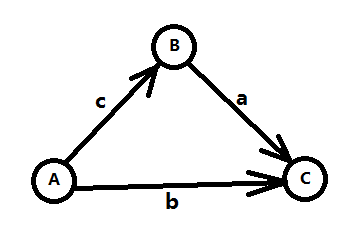
图三-2-1
我们发现min{b, a+c}正好对应了A到C的最短路,而这三个不等式就是著名的三角不等式。将三个不等式推广到m个,变量推广到n个,就变成了n个点m条边的最短路问题了。
3、解的存在性
上文提到最短路的时候,会出现负权圈或者根本就不可达的情况,所以在不等式组转化的图上也有可能出现上述情况,先来看负权圈的情况,如图三-3-1,下图为5个变量5个不等式转化后的图,需要求得是X[t] - X[s]的最大值,可以转化成求s到t的最短路,但是路径中出现负权圈,则表示最短路无限小,即不存在最短路,那么在不等式上的表现即X[t] - X[s] <= T中的T无限小,得出的结论就是 X[t] - X[s]的最大值 不存在。

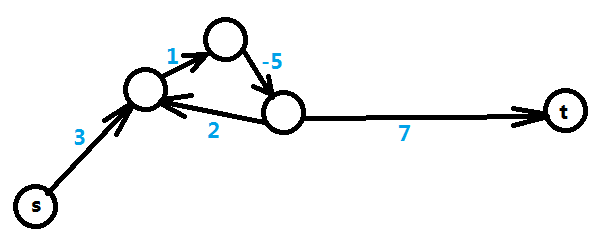
图三-3-1
再来看另一种情况,即从起点s无法到达t的情况,如图三-3-2,表明X[t]和X[s]之间并没有约束关系,这种情况下X[t] - X[s]的最大值是无限大,这就表明了X[t]和X[s]的取值有无限多种。

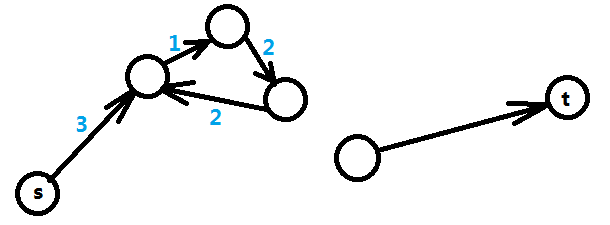
图三-3-2
在实际问题中这两种情况会让你给出不同的输出。综上所述,差分约束系统的解有三种情况:1、有解;2、无解;3、无限多解;
4、最大值 => 最小值
然后,我们将问题进行一个简单的转化,将原先的"<="变成">=",转化后的不等式如下:
B - A >= c (1)
C - B >= a (2)
C - A >= b (3)
然后求C - A的最小值,类比之前的方法,需要求的其实是max{b, c+a},于是对应的是图三-2-1从A到C的最长路。同样可以推广到n个变量m个不等式的情况。 5、不等式标准化
如果给出的不等式有"<="也有">=",又该如何解决呢?很明显,首先需要关注最后的问题是什么,如果需要求的是两个变量差的最大值,那么需要将所有不等式转变成"<="的形式,建图后求最短路;相反,如果需要求的是两个变量差的最小值,那么需要将所有不等式转化成">=",建图后求最长路。
如果有形如:A - B = c 这样的等式呢?我们可以将它转化成以下两个不等式:
A - B >= c (1)
A - B <= c (2)
再通过上面的方法将其中一种不等号反向,建图即可。 最后,如果这些变量都是整数域上的,那么遇到A - B < c这样的不带等号的不等式,我们需要将它转化成"<="或者">="的形式,即 A - B <= c - 1。
三、差分约束的经典应用
1、线性约束
线性约束一般是在一维空间中给出一些变量(一般定义位置),然后告诉你某两个变量的约束关系,求两个变量a和b的差值的最大值或最小值。
【例题1】N个人编号为1-N,并且按照编号顺序排成一条直线,任何两个人的位置不重合,然后给定一些约束条件。
X(X <= 100000)组约束Ax Bx Cx(1 <= Ax < Bx <= N),表示Ax和Bx的距离不能大于Cx。
Y(X <= 100000)组约束Ay By Cy(1 <= Ay < By <= N),表示Ay和By的距离不能小于Cy。
如果这样的排列存在,输出1-N这两个人的最长可能距离,如果不存在,输出-1,如果无限长输出-2。
像这类问题,N个人的位置在一条直线上呈线性排列,某两个人的位置满足某些约束条件,最后要求第一个人和最后一个人的最长可能距离,这种是最直白的差分约束问题,因为可以用距离作为变量列出不等式组,然后再转化成图求最短路。
令第x个人的位置为d[x](不妨设d[x]为x的递增函数,即随着x的增大,d[x]的位置朝着x正方向延伸)。
那么我们可以列出一些约束条件如下:
1、对于所有的Ax Bx Cx,有 d[Bx] - d[Ax] <= Cx;
2、对于所有的Ay By Cy,有 d[By] - d[Ay] >= Cy;
3、然后根据我们的设定,有 d[x] >= d[x-1] + 1 (1 < x <= N) (这个条件是表示任何两个人的位置不重合)
而我们需要求的是d[N] - d[1]的最大值,即表示成d[N] - d[1] <= T,要求的就是这个T。
于是我们将所有的不等式都转化成d[x] - d[y] <= z的形式,如下:
1、d[Bx] - d[Ax] <= Cx
2、d[Ay] - d[By] <= -Cy
3、d[x-1] - d[x] <= -1
对于d[x] - d[y] <= z,令z = w(y, x),那么有 d[x] <= d[y] + w(y, x),所以当d[x] > d[y] + w(y, x),我们需要更新d[x]的值,这对应了最短路的松弛操作,于是问题转化成了求1到N的最短路。
对于所有满足d[x] - d[y] <= z的不等式,从y向x建立一条权值为z的有向边。
然后从起点1出发,利用SPFA求到各个点的最短路,如果1到N不可达,说明最短路(即上文中的T)无限长,输出-2。如果某个点进入队列大于等于N次,则必定存在一条负环,即没有最短路,输出-1。否则T就等于1到N的最短路。
2、区间约束
【例题2】给定n(n <= 50000)个整点闭区间和这个区间中至少有多少整点需要被选中,每个区间的范围为[ai, bi],并且至少有ci个点需要被选中,其中0 <= ai <= bi <= 50000,问[0, 50000]至少需要有多少点被选中。
例如3 6 2 表示[3, 6]这个区间至少需要选择2个点,可以是3,4也可以是4,6(总情况有 C(4, 2)种 )。
这类问题就没有线性约束那么明显,需要将问题进行一下转化,考虑到最后需要求的是一个完整区间内至少有多少点被选中,试着用d[i]表示[0, i]这个区间至少有多少点能被选中,根据定义,可以抽象出 d[-1] = 0,对于每个区间描述,可以表示成d[ bi ] - d[ ai - 1 ] >= ci,而我们的目标要求的是 d[ 50000 ] - d[ -1 ] >= T 这个不等式中的T,将所有区间描述转化成图后求-1到50000的最长路。
这里忽略了一些要素,因为d[i]描述了一个求和函数,所以对于d[i]和d[i-1]其实是有自身限制的,考虑到每个点有选和不选两种状态,所以d[i]和d[i-1]需要满足以下不等式: 0 <= d[i] - d[i-1] <= 1 (即第i个数选还是不选)
这样一来,还需要加入 50000*2 = 100000 条边,由于边数和点数都是万级别的,所以不能采用单纯的Bellman-Ford ,需要利用SPFA进行优化,由于-1不能映射到小标,所以可以将所有点都向x轴正方向偏移1个单位(即所有数+1)。
3、未知条件约束
未知条件约束是指在不等式的右边不一定是个常数,可能是个未知数,可以通过枚举这个未知数,然后对不等式转化成差分约束进行求解。
【例题3】
四、差分约束题集整理
在一家超市里,每个时刻都需要有营业员看管,R(i) (0 <= i < 24)表示从i时刻开始到i+1时刻结束需要的营业员的数目,现在有N(N <= 1000)个申请人申请这项工作,并且每个申请者都有一个起始工作时间 ti,如果第i个申请者被录用,那么他会连续工作8小时。
现在要求选择一些申请者进行录用,使得任何一个时刻i,营业员数目都能大于等于R(i)。
i = 0 1 2 3 4 5 6 ... 20 21 22 23 23,分别对应时刻 [i, i+1),特殊的,23表示的是[23, 0),并且有些申请者的工作时间可能会“跨天”。
a[i] 表示在第i时刻开始工作的人数,是个未知量
b[i] 表示在第i时刻能够开始工作人数的上限, 是个已知量
R[i] 表示在第i时刻必须值班的人数,也是已知量
那么第i时刻到第i+1时刻还在工作的人满足下面两个不等式(利用每人工作时间8小时这个条件):
当 i >= 7, a[i-7] + a[i-6] + ... + a[i] >= R[i] (1)
当 0 <= i < 7, (a[0] + ... + a[i]) + (a[i+17] + ... + a[23]) >= R[i] (2)
对于从第i时刻开始工作的人,满足以下不等式:
0 <= i < 24, 0 <= a[i] <= b[i] (3)
令 s[i] = a[0] + ... + a[i],特殊地,s[-1] = 0
上面三个式子用s[i]来表示,如下:
s[i] - s[i-8] >= R[i] (i >= 7) (1)
s[i] + s[23] - s[i+16] >= R[i] (0 <= i < 7) (2)
0 <= s[i] - s[i-1] <= b[i] (0 <= i < 24) (3)
仔细观察不等式(2),有三个未知数,这里的s[23]就是未知条件,所以还无法转化成差分约束求解,但是和i相关的变量只有两个,对于s[23]的值我们可以进行枚举,令s[23] = T, 则有以下几个不等式:
s[i] - s[i-8] >= R[i]
s[i] - s[i+16] >= R[i] - T
s[i] - s[i-1] >= 0
s[i-1] - s[i] >= -b[i]
对于所有的不等式 s[y] - s[x] >= c,建立一条权值为c的边 x->y,于是问题转化成了求从原点-1到终点23的最长路。
但是这个问题比较特殊,我们还少了一个条件,即:s[23] = T,它并不是一个不等式,我们需要将它也转化成不等式,由于设定s[-1] = 0,所以 s[23] - s[-1] = T,它可以转化成两个不等式:
s[23] - s[-1] >= T
s[-1] - s[23] >= -T
将这两条边补到原图中,求出的最长路s[23]等于T,表示T就是满足条件的一个解,由于T的值时从小到大枚举的(T的范围为0到N),所以第一个满足条件的解就是答案。
最后,观察申请者的数量,当i个申请者能够满足条件的时候,i+1个申请者必定可以满足条件,所以申请者的数量是满足单调性的,可以对T进行二分枚举,将枚举复杂度从O(N)降为O(logN)。
最短路
Shortest Path ★☆☆☆☆ 单源最短路
Shortest Path Problem ★☆☆☆☆ 单源最短路 + 路径数
HDU Today ★☆☆☆☆ 单源最短路
Idiomatic Phrases Game ★☆☆☆☆ 单源最短路
Here We Go(relians) Again ★☆☆☆☆ 单源最短路
find the safest road ★☆☆☆☆ 单源最短路
Saving James Bond ★☆☆☆☆ 单源最短路
A strange lift ★☆☆☆☆ 单源最短路
Free DIY Tour ★☆☆☆☆ 单源最短路 + 路径还原
find the safest road ★☆☆☆☆ 单源最短路(多询问)
Invitation Cards ★★☆☆☆ 单源最短路
Minimum Transport Cost ★★☆☆☆ 单源最短路 + 路径还原
Bus Pass ★★☆☆☆ 单源最短路
In Action ★★☆☆☆ 单源最短路 + 背包
Choose the best route ★★☆☆☆ 单源最短路 + 预处理
find the longest of the shortest ★★☆☆☆ 二分枚举 + 最短路
Cycling ★★☆☆☆ 二分枚举 + 最短路
Trucking ★★☆☆☆ 二分枚举 + 最短路
Delay Constrained Maximum Capacity ★★☆☆☆ 二分枚举 + 最短路
The Worm Turns ★★☆☆☆ 四向图最长路
A Walk Through the Forest ★★☆☆☆ 按照规则求路径数
find the mincost route ★★☆☆☆ 无向图最小环
Arbitrage ★★☆☆☆ 多源最短路
zz's Mysterious Present ★★☆☆☆ 单源最短路
The Shortest Path ★★☆☆☆ 多源最短路
Bus System ★★★☆☆ 单源最短路
How Many Paths Are There ★★★☆☆ 次短路
WuKong ★★★☆☆ 两条最短路的相交点个数为P,要求最大化P
Shortest Path ★★★☆☆ 多询问的最短路
Sightseeing ★★★☆☆ 最短路和次短路的路径数
Travel ★★★☆☆ 最短路径树思想
Shopping ★★★☆☆
Transit search ★★★★☆
Invade the Mars ★★★★☆
Circuit Board ★★★★☆
Earth Hour ★★★★☆
Catch the Theves ★★★★☆
差分约束
Layout ★★☆☆☆ 差分约束系统 - 最短路模型 + 判负环
World Exhibition ★★☆☆☆ 差分约束系统 - 最短路模型 + 判负环
House Man ★★☆☆☆ 差分约束系统 - 最短路模型 + 判负环
Intervals ★★☆☆☆ 差分约束系统 - 最长路模型 边存储用链式前向星
King ★★☆☆☆ 差分约束系统 - 最长路模型 + 判正环
XYZZY ★★☆☆☆ 最长路 + 判正环
Integer Intervals ★★☆☆☆ 限制较强的差分约束 - 可以贪心求解
THE MATRIX PROBLEM ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
Is the Information Reliable? ★★★☆☆ 差分约束系统 - 最长路模型 + 判正环
Advertisement ★★★☆☆ 限制较强的差分约束 - 可以贪心求解
Cashier Employment ★★★☆☆ 二分枚举 + 差分约束系统 - 最长路模型
Schedule Problem ★★★☆☆ 差分约束系统 - 最长路模型
Candies ★★★☆☆
Burn the Linked Camp ★★★☆☆
Instrction Arrangement ★★★☆☆