『数据结构总结1:树状数组』
Preface
数据结构的总结可能就会以这种形式分好几篇发了,吸取了之前的教训,防止编辑器变卡.
如果后继总结更新了,链接会补在这里.
原理
树状数组是一种用于维护序列前缀和的数据结构,对于给定序列({a_i}),建立序列({c_i})定义如下:
对于一个任意的正整数(n),我们都可以根据其二进制上为(1)的位,利用(mathrm{lowbit})运算,将([1,n])划分为不超过(log_2 n)个区间. 那么前缀和就可以用这(log_2n)个区间和的和表示,根据序列({c_i})的定义,我们可以轻松地在(mathcal{O}(log_2n))的时间内求一个序列的前缀和.
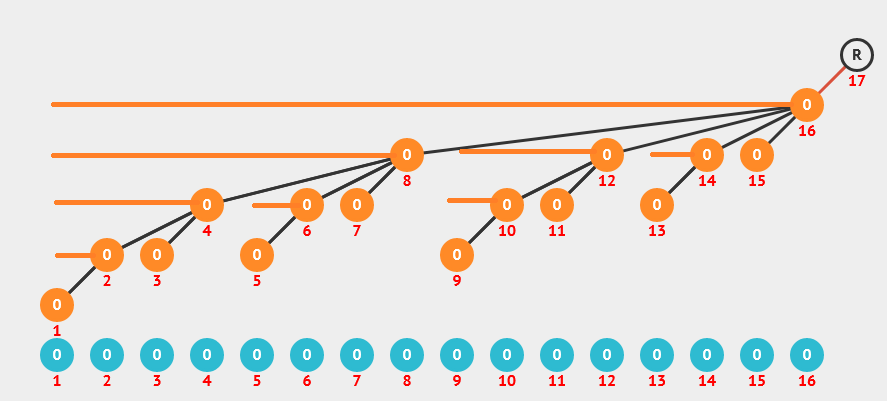
对于单点修改,我们只需考察那些(c_x)会被当前修改的值所影响. 我们可以将({c_i})看做一个树形结构(森林),每个点(c_i)占据区间([i-mathrm{lowbit}(i)+1,i]),同时向其内部所有最大的,可以表示其区间和的(c_j)连边. 那么显然一个点的修改会对树上所有祖先有影响,同时不难发现一个性质节点(c_i)的父亲为(c_{i+mathrm{lowbit(i)}}),那么修改操作就容易实现了. 根据(mathrm{lowbit})函数的性质,其时间复杂度显然也是(mathcal{O}(log_2 n)).
实现
struct BinaryIndexedTree
{
int c[N],n;
inline int lowbit(int x) { return x & (-x); }
inline void Modify(int p,int v) { for (; p <= n; p += lowbit(p)) c[p] += v ); }
inline int Query(int p) { int s = 0; for (; p; p -= lowbit(p)) s += c[p]; return s; }
inline int Query(int l,int r) { return Query(r) - Query(l-1); }
}
不必过多解释,唯一需要注意的地方是(mathrm{lowbit}(0)=0),所以单点修改时如果涉及到下标(0),需要进行整体平移,否则会死循环.
功能
单点修改,区间查询
基本操作,时间复杂度均为(mathcal{O}(log_2n)).
区间修改,单点查询
不妨对原序列进行差分,那么在原序列上的操作((l,r,+x))对差分序列({d_n})的影响为(l)位置(+x),(r+1)位置(-x). 单点查询在差分序列上的体现为前缀和.
区间修改,区间查询
同样求其差分序列({d_n}),修改操作同上执行. 我们只需考虑如何求和:
维护({d_i})和({d_i imes i})两个前缀和即可.
后缀操作
将修改函数和求和函数的遍历顺序反过来即可.
区间修改,区间最值
类似于线段树,从(mathcal{O}(log_2n))个儿子处获取信息,并下传懒标记,时间复杂度(mathcal{O}(log^2 n)),无实际意义.
当操作只有单点修改,前缀最值(/)后缀最值查询时,可以直接按照原来的方式处理,时间复杂度(mathcal{O}(log_2n)).
维护二维平面
定义
其他概念类似,可以用完全一样的方式实现单点修改,矩阵求和,时间复杂度(mathcal{O}(log^2 n)),空间复杂度(mathcal{O}(n^2)).
定义二维差分(d_{i,j}=a_{i,j}-a_{i-1,j}-a_{i,j-1}+a_{i-1,j-1}),显然满足(a_{n,m}=sum_{i=1}^nsum_{j=1}^m d_{i,j}). 现对原矩阵差分,则矩阵修改((x_1,x_2,y_1,y_2,+p))在差分矩阵上的影响为((x_1,y_1,+p),(x_1,y_2+1,-p),(x_2+1,y_1,-p),(x_2+1,y_2+1,+p)). 那么容易实现矩阵修改,单点查询.
现在我们用差分实现矩阵修改,同理,考虑用差分矩阵的值表示原矩阵的一个前缀矩阵和:
维护({d_{i,j}}),({i imes d_{i,j}}),({j imes d_{i,j}}),({i imes j imes d_{i,j}})四个矩阵和即可实现矩阵修改,矩阵查询.
值域树状数组
值域树状数组可以实现简易平衡树的功能,维护排名就是前缀和,插入删除一个数字就是单点修改,现在我们考虑求(k)大值.
考虑倍增,每次我们尝试向前(2^i)走步,(i)从大到小枚举. 现在假设答案为(p),那么我们想知道区间([k,k+2^i])里有几个数. 如果有(i<mathrm{lowbit}(k)),那么根据定义(c_{k+2^i})存储的就是我们要的值. 好在倍增算法从大到小枚举(i),所以(k)累加的过程也是从高位到低位的,恰好符合我们的需求. 那么倍增求第(k)大,时间复杂度(mathcal{O}(log_2 n)).
inline int Select(int k)
{
int res = 0 , cnt = 0;
for (int i = 30; res += (1<<i) , i >= 0; i--)
( res > lim || cnt + c[res] >= k ) ? res -= 1<<i : cnt += c[res];
return ++res; // if the size of BIT less than k , return size + 1
}