题目链接
题目大意
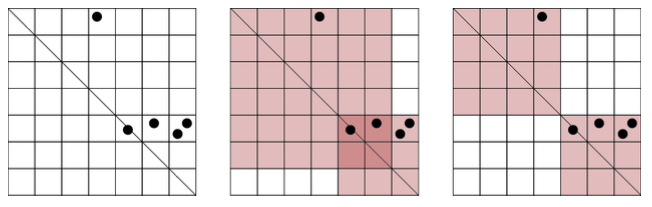
在一个 (M imes M) 的正方形网格图上分布着 (N) 个关键点,你需要选择至多 (K) 个两端点在主对角线上的正方形去覆盖它们,在这种情况下,求最少要覆盖多少个方格。
(1leq N leq 10^5),(1leq Mleq 10^6),(1leq kleq N)
思路
为了方便,我们把点全部翻到主对角线下方(即 (igeq j) 的位置),注意到对于点 (x) 和 (y) ,若 (r_xleq r_y) 且 (c_xgeq c_y),则当 (y) 被覆盖后, (x) 必然在其正方形中,所以 (x) 是没有考虑的价值的,可以按 (r_i) 排序后用栈去重。
剩下的点组成了一条单调下降的折线,设 (nxt_i) 为第 (i) 个点下面那个点的横坐标,若后来一个正方形要覆盖点 (i) 以下的一块区域,那么只需要盖到 (nxt_i) 的地方即可,同时令 (loc_i) 为第 (i) 个点的纵坐标。设 (f_{i,k}) 为用 (k) 个正方形覆盖前 (i) 个节点最少需要覆盖的方格数,可以得到转移式:
((i-nxt_j+1)^2) 为新添加正方形的大小,(max{0,j-nxt_j+1}^2) 为此正方形和上一个重合的区域。
这个平方带有很强的提示性,展开:
令 (g_{j,k} = (nxt_j-1)^2+f_{j,k}-max{0,loc_j-nxt_j+1}^2),去掉 (min) :
由于 (nxt_j-1) 和 (2loc_i) 都是单调递增的,所以可以直接用队列维护凸包,把 (dp) 斜率优化到 (O(NK)) 。
但是这样还是不够快,我们需要摆脱 (K) 的影响,这里需要使用 (wqs) 二分优化,不会的可以去 这里 看看。
通过打表(感性理解)可以发现,选 (k) 个正方形时的答案 (ans_k) 是一个关于 (k) 的一个凸性函数,其导数单调递减,直观感受就是当已经选的正方形越多,再给正方形所能做到的优化就越来越小了,这个结论我本身想尝试去证的,但是真的有点难证。。就连官方题解说的都是


有了这个性质就可以 (wqs) 二分了,我们给添加一个正方形这个操作额外增加一个权值 (C),当 (C = 0) 时,函数的最高点的横坐标 (V(C)=N),当 (C = M^2) 时,(V(C)=1),这是二分的下界和上界,我们二分找到最大的 (C) 使得 (V(C)leq K),则答案即为 (f_{tot,K}-Kcdot C) 。
时间复杂度: (O(N(logN+logM)))
一些细节
-
单调栈去点的时候要注意点在同一行上的情况,如果你用 (pair) 排序,你会发现这里不是你想要的顺序,需要判断一下。
-
有一个 (wqs) 二分初学者容易搞错的地方,二分中的那个凸包是辅助说明其正确性所为,实际实现时不需要考虑,是隐性的。这里找最高点时正常 (dp) 就可以了,且不需要 (k) 这一维,转移时记录一下用了几个正方形。
-
由于不一定能找到最高点恰好是 (K),但是找不到的情况只发生在 (ans_k) 于 (kin[V(C),V(C+1)]) 之间是等差的情况,这时有
[f_{tot,V(C)}-Ccdot V(C)=ans_{V(C)}=f_{tot,K}-Ccdot K ]这是最后一步答案计算的依据,不过要注意的是我们必须找到最小的 ”最大值发生的地方“ 作为 (V(C)),具体点说就是斜率优化中比较斜率淘汰队头时,条件必须是大于,而不是大于等于。
-
几乎所有地方都要开long long,本人在二分上下界的地方忘开了。。
Code
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<queue>
#include<stack>
#include<fstream>
#define rep(i,a,b) for(int i = (a); i <= (b); i++)
#define per(i,b,a) for(int i = (b); i <= (a); i++)
#define N 100100
#define ll long long
#define PLL pair<ll, ll>
#define fr first
#define sc second
#define Inf 0x3f3f3f3f
using namespace std;
inline int read(){
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') s = (s<<3)+(s<<1)+(ch^48), ch = getchar();
return s*w;
}
ll n, m, k, cnt;
ll nxt[N], g[N], loc[N];
PLL P[N], f[N];
void init(){
rep(i,1,n) if(P[i].fr < P[i].sc)
swap(P[i].fr, P[i].sc);
sort(P+1, P+n+1);
stack<PLL> s;
s.push({-1, -1});
rep(i,1,n){
while(!s.empty() && s.top().sc >= P[i].sc) s.pop();
if(s.top().fr != P[i].fr) s.push(P[i]);
}
int lst = Inf;
while(!s.empty()){
nxt[cnt] = lst;
lst = s.top().sc, loc[cnt++] = s.top().fr;
s.pop();
}
reverse(nxt, nxt+cnt), reverse(loc, loc+cnt);
}
void get_G(int i){
g[i] = (nxt[i]-1)*(nxt[i]-1) + f[i].fr;
if(loc[i]-nxt[i]+1 > 0) g[i] -= (loc[i]-nxt[i]+1)*(loc[i]-nxt[i]+1);
}
double K(int i, int j){
return 1.0*(g[i]-g[j])/(nxt[i]-nxt[j]);
}
int cal(ll Cost){
static int q[N];
int l = 0, r = 0;
q[0] = 0, get_G(0);
rep(i,1,cnt-1){
ll x = loc[i];
while(l < r && K(q[l], q[l+1]) < 2*x) l++;
f[i].fr = g[q[l]]-2*x*(nxt[q[l]]-1)+x*x + Cost, f[i].sc = f[q[l]].sc+1;
get_G(i);
while(l < r && K(q[r-1], q[r]) >= K(q[r], i)) r--;
q[++r] = i;
}
return f[cnt-1].sc;
}
ll solve(){
ll l = 0, r = m*m, mid;
while(l < r){
mid = (l+r)>>1;
if(cal(mid) <= k) r = mid;
else l = mid+1;
}
cal(l);
return f[cnt-1].fr - l*k;
}
ll take_photos(int _n, int _m, int _k, vector<int> r, vector<int> c){
n = _n, m = _m, k = _k;
rep(i,0,r.size()-1) P[i+1].fr = r[i], P[i+1].sc = c[i];
init();
return solve();
}
int main(){
cin>>n>>m>>k;
vector<int> c(n), r(n);
rep(i,0,n-1) c[i] = read(), r[i] = read();
cout<<take_photos(n, m, k, r, c)<<endl;
return 0;
}
一点小经验:犯了 “一些细节” 中第3条中的错误后,代码在随机数据上仍然可以跑的相当优秀,当时拍了 (9000) 多组极限数据都没有拍出错,不过在跑 (Nleq10),(Mleq20) 的特殊性质数据时马上挂了。