题目链接:AcWing 380. 舞动的夜晚
题目大意:
有一张左部 (N) 个点,右部 (M) 个点,(T) 条边的二分图,求在强制连哪些边后,图的最大匹配会减小。
(1leq N,M leq 10000) , (1leq Tleq 100000) 。
思路:
引入两个概念:二分图的必需边和可行边。
- 必需边:删除之后会影响最大匹配的边。
- 可行边:出现在至少一个最大匹配方案中的边。
先说他们该如何判定,我们先用最大流求出二分图的一个可行解,得到残余网络,我们画一下图:

这时 (1) 和 (3) 匹配, (2) 和 (4) 匹配,注意到在这种情况下,((1,3)) 和 ((2,4)) 都不可能是必需边,因为它俩不匹配,可以被另外的边替代:
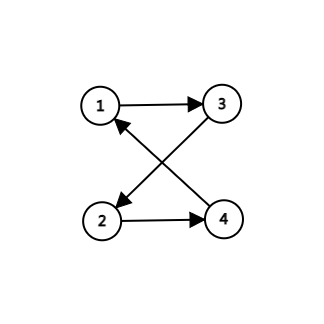
这样可以类推得到结论:
必需边 (Leftrightarrow) 在残留网络上为匹配边且两端点不属于同一个强连通分量
可行边 (Leftrightarrow) 在残留网络上为匹配边或两端点在同一个强连通分量内
而这道题求的就是不可行边,即可行边的补集, (Dinic) 最大流 (+) (Tarjan) 强连通分量 就做完了。
时间复杂度 (O(T sqrt{N+M})) 。
Code:
#include<iostream>
#include<cstring>
#include<queue>
#include<stack>
#define mem(a,b) memset(a,b,sizeof(a))
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define per(i,b,a) for(int i=b;i>=a;i--)
#define N 20010
#define E 200200
#define Inf 0x3f3f3f3f3f
using namespace std;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9')s=(s<<3)+(s<<1)+(ch^48),ch=getchar();
return s*w;
}
int head[N],to[E],nxt[E];
int cnt,n,m,e,s,t;
int cap[E],d[N];
int c[N],dfn[N],low[N],scc,num;
int rlt[N][3]; //short for "relation"
bool in[N];
queue<int> q;
stack<int> st;
void init(){mem(head,-1),cnt=-1;}
void add_e(int a,int b,bool id){
nxt[++cnt]=head[a],head[a]=cnt,to[cnt]=b,cap[cnt]=id;
if(id)add_e(b,a,0);
}
bool bfs(){
mem(d,0);
while(!q.empty())q.pop();
q.push(s),d[s]=1;
while(!q.empty()){
int cur=q.front(); q.pop();
for(int i=head[cur];~i;i=nxt[i])
if(cap[i]&&!d[to[i]]){
q.push(to[i]);
d[to[i]]=d[cur]+1;
if(to[i]==t)return true;
}
}
return false;
}
int dinic(int x,int flow){
if(x==t)return flow;
int rest=flow,k;
for(int i=head[x];(~i)&&rest;i=nxt[i]){
if(cap[i]&&d[to[i]]==d[x]+1){
k=dinic(to[i],min(rest,cap[i]));
if(!k)d[to[i]]=0; //弧优化
cap[i]-=k,cap[i^1]+=k,rest-=k;
}
}
return flow-rest;
}
void tarjan(int x){
low[x]=dfn[x]=++num;
st.push(x),in[x]=true;
for(int i=head[x];~i;i=nxt[i]){
if(!cap[i])continue;
int y=to[i];
if(!dfn[y]){
tarjan(y);
low[x]=min(low[x],low[y]);
}else if(in[y])
low[x]=min(low[x],dfn[y]);
}
if(dfn[x]==low[x]){
scc++; int y;
do{
y=st.top(),st.pop();
in[y]=false,c[y]=scc;
}while(y!=x);
}
}
int main(){
cin>>n>>m>>e;
init();
int a,b;
rep(i,1,e){
rlt[i][0]=a=read(),rlt[i][1]=b=read();
rlt[i][2]=cnt+1;
add_e(a,b+n,1);
}
s=0,t=m+n+1;
rep(i,1,n)add_e(s,i,1);
rep(i,1,m)add_e(i+n,t,1);
int flow,maxflow;
while(bfs()){
while(flow=dinic(s,Inf))maxflow+=flow;
}
rep(i,0,n+m+1){
if(!dfn[i])tarjan(i);
}
int ans=0;
rep(i,1,e){
int u=rlt[i][0],v=rlt[i][1]+n;
if(!cap[rlt[i][2]]||c[u]==c[v])ans++;
}
cout<<e-ans<<endl;
rep(i,1,e){
int u=rlt[i][0],v=rlt[i][1]+n;
if(cap[rlt[i][2]]&&c[u]!=c[v])cout<<i<<" ";
}
return 0;
}