出自某模拟赛。
题目大意:
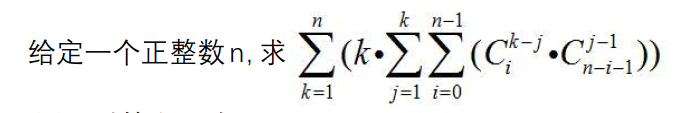
对1e9+7取模。
数据范围
20 % : n<=300
40 % : n<=2,000
50 % : n<=10,000
70 % : n<=1,000,000
100 % : n<=1,000,000,000
题解
方法众多。
然而我太蒟了,2h43min愣是写了一个40pts暴力走人。
开始指着想正解,但是发现想不出来,然后写n^2暴力,结果总是要么漏算要么算重要么取模出错。。。最后才调出来。
1.如果比较菜,请尝试打表:
$n^3$暴力显然。然后打表。
$n=1,ans_1=1$
$n=2,ans_2=6$
$n=3,ans_3=24$
$n=4,ans_4=80$
然后,套路的先观察相邻两项的关系。
然后尝试和项数的下标套上关系。
$ans_2=ans_1 imes frac{6}{1}$
$ans_3=ans_2 imes frac{8}{2}$
$ans_4=ans_3 imes frac{10}{3}$
诶,然后发现了规律!!
可以递推。
$f_{n+1}=f_n imes frac{4+2 imes n}{n}$
$f_{n+1}=f_n imes frac{2 imes(n+2)}{n}$
迭代下去得:
$f_{n+1}=f_1 frac{2^n imes (n+2)!}{2n!}$
$f_{n+1}=frac{2^{n} imes (n+1) imes(n+2)}{2}$
$f_{n}=frac{2^{n-1} imes n imes(n+1)}{2}$
即可出结果
2.正解:
有点意思的是,i+n-i-1=n-1,k-j+j-1=k-1对于任意的i,j恒成立。
这就是突破口
考虑组合数的意义。
$sum_{k=1}^n(k imessum_{j=1}^ksum_{i=0}^{n-1}(C_i^{k-j} imes C_{n-i-1}^{j-1})$
$=sum_{k=1}^n(k imessum_{i=0}^{n-1}sum_{j=1}^k(C_i^{k-j} imes C_{n-i-1}^{j-1})$
j和i换了位置之后,
发现,其实i就是枚举的一个分割点,
然后对于选择的k-1个数,在1~i个数中选择k-j个,
在i+1~n-i-1个数中选择j-1个。
好像和$C_{n-1}^{k-1}$有些关系。
发现,对于$C_{n-1}^{k-1}$中的每个方案。
其实都可以找出0~n-1这n个分界点,然后统计一次。
每个方案被统计了n次。
所以,
原式
$=sum_{k=1}^nk imes n imes C_{n-1}^{k-1}$
已经可以O(n)递推了。
我们可以用刚才的打表中方法,搞出递推式,然后迭代出来通项公式。
即可O(logn)求解。
3.但是这个还不够漂亮!!!
这个可是组合数啊!!不是一般的数。
组合数毕竟有实际的意义。
观察这个式子的组合意义。
$sum_{k=1}^nk imes n imes C_{n-1}^{k-1}$
这个k-1和k,n有点麻烦。
提出来:
$=n imes (sum_{k=1}^n(k-1) imes C_{n-1}^{k-1})+n imes 2^{n-1}$
第一个括号里面是什么意义?
对于n-1个数的集合中,所有子集的大小的和。
套路地,我们转化研究对象。
考虑每个元素被统计了几次。
就是:$2^{n-1-1}=2^{n-2}$
因为每个数自己必须出现一次,然后其他的数爱出现不出现。
所以,
$=n imes( (n-1) imes2^{n-2})+n imes 2^{n-1}$
然后就可以O(logn)计算了。
总结:
0.这个式子,我们尝试用数学知识、组合数公式化简,发现不容易化简。然后就要考虑组合数的意义。
1.组合数是一个有意义的数。这样的数学式子的推导,可以通过寻找式子的意义来进行化简。
往往起到立竿见影的效果。
2.打表找规律,要考虑把结果,递推关系和项的编号放在一起。