线段树原理
线段树是一颗二叉树,他的每个节点对应的都是一个区间,主要是通过对区间的分割和合并来修改节点的值, 然后再得到答案。
现在给你一个 目的为求区间和 所造出来的线段树 线段树。如下图所示。
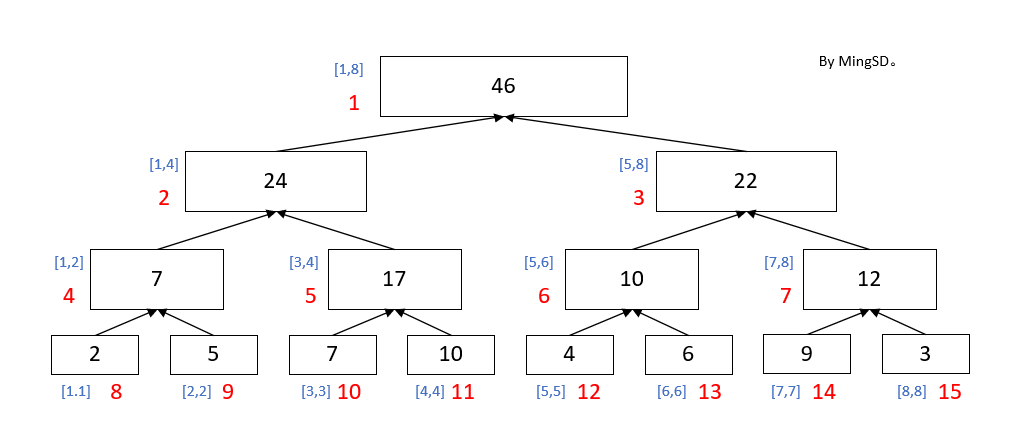
仔细观察,第一二三行方框内的值是他的下面2个子区间的和, 第四行的方框内的数字代表的是自身的值, 蓝色代表的是这个方框他包含的区间, 红色代表的是这个元素在数组中所储存的位置。(在绝大多数博客中,我们默认区间的左儿子他的下标是当前区间下标的2倍,右儿子的下标是当前区间的2倍再加上1,这个下标是认为定义的,你也可以将对应关系修改)。
为什么说用线段树可以节省求和时间呢, 假设我们需要查找区间 [1,8] 的和, 对于这个不用多说, 我们可以直接将最上面的那个46输出,因为最上面的那个矩形代表的就是区间 [1,8] 的和。
然后假设我们要查找区间 [3,7] 的和, 刚开始我们出现在区间 [1,8]的位置, 但是对于目标区间来说 [1,8] 太大了, 所以我们要继续往下走, 走到 [1,4] 和 [5,8] 的区间, 但是对于这2个区间来说, 还有一部分区域是落在查询区间之外的, 所以我们需要继续往下走,我们先分析区间 [1,4] , 对于他左儿子的区间[1,2]来说,没有任意一个点是落在查询区间内的, 所以我们不需要走到他的左儿子处, 然后走到右儿子[3,4],可以发现 [3,4] 倍查询区间覆盖了, 所以我们就不需要往下走了, 因为整个区间都倍覆盖了, 直接将这个点的值返回就好了, 因为这个点就是他下面节点的和。 然后我们再看区间[5,8], 先往左走, 走到左儿子区间 [5,6] ,也可以发现该区间倍查询区间覆盖了,就不需要往下走了, 返回该节点的值,对于右儿子节点 [7,8] 来说,只有一部分区域倍查询区间覆盖, 所以我们还需要往下走,继续往左边走, 发现 [7,7] 是合法区域, 返回该值, {8,8]不是合法区域,所以不对这快里的数据进行处理。 所以最后的结果就是 [3,4] + [5,6] + [7,7] 这3个区间的和。 可能你会说就5个点而已, 我直接加过去时间也就这样, 的确, 当点数小的时候线段树的优势并不会很明显,但是如果查询的区间长度会到达 1e5的话, 那么线段树就可以省下很多时间了。
线段树的某段区间内的值是可以修改的。
假设我们修改了区间[2,2]的值
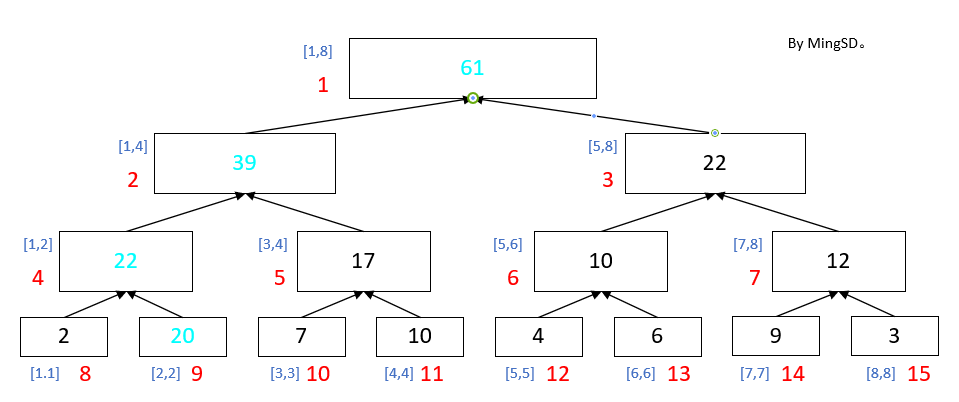
我们就需要更新一下所有区间内含2的区间, 也就是顺着[2,2]一直往上走 按次序更新 [2,2] -> [1,2] -> [1,4] -> [1,8] 这四个区间的值, 更新完了之后就可以继续愉快的去查询区间和了。
可以发现, 每一次对于一个点更新之后, 她执行的点的数目就是logn个, 如果你使用的是前缀和去写的话, 就需要约更新n 个节点。
代码实现
1,建树,对于一颗树需要先建树。这里用到的是递归建树。

1 void Build(int l, int r, int rt){ // l,r 代表的是这个区间内的左端点 和 右端点, rt代表的是 [l,r] 这个区间内的值是存在哪一个位置的。 2 if(l == r){ 3 scanf("%d", tree[rt]); /// tree[rt] = a[l]; 4 return ; 5 } 6 int m = (l+r) / 2; 7 Build(l,m,rt*2); // 对于区间区分,我们一般将m点划入左半边区间 8 Build(m+1,r,rt*2+1); 9 PushUp(rt); // PushUp 函数是通过2个子节点来更新现在这个节点的状态, 对于不同的要求需要不同的写法。 10 }

1 void Build(int l, int r, int rt){ 2 if(l == r){ 3 scanf("%d", tree[rt]); /// tree[rt] = a[l]; 4 return ; 5 } 6 int m = (l+r) / 2; 7 Build(l,m,rt*2); 8 Build(m+1,r,rt*2+1); 9 PushUp(rt); 10 }
2,通过子节点来更新目前节点。

1 void PushUp(int rt){ 2 tree[rt] = tree[rt*2] + tree[rt*2+1]; ///区间和的更新操作 3 } 4 void PushUp(int rt){ 5 tree[rt] = max(tree[rt*2], tree[rt*2+1]);///求区域最大值的更新操作 6 }

1 void PushUp(int rt){ 2 tree[rt] = tree[rt*2] + tree[rt*2+1]; 3 } 4 void PushUp(int rt){ 5 tree[rt] = max(tree[rt*2], tree[rt*2+1]); 6 }
3,更新某个节点。

1 void Update(int l, int r, int rt, int L, int C){ // l,r,rt 与前面的定义一样, L代表的是要更新区间的位置,C代表的是修改后的值 2 if(l == r){ /// 这里不能写成 if(l == L) 因为有可能左端点恰好是要更新的位置, 但是还有右端点, 我们直接更新的只有区间 [L,L]。 3 tree[rt] = C; 4 return ; 5 } 6 int m = (l+r) / 2; 7 if(L <= m) Update( l, m, rt*2, L, C); //要更新的区间在左边部分,所以往左边走,更新左边 8 else Update(m+1, r, rt*2+1, L, C); //要更新的区间在右边部分, 往右边走,更新右边 9 PushUp(rt); //更新完子节点之后需要更新现在的位置, 需要保证线段树的性质。 10 }

1 void Update(int l, int r, int rt, int L, int C){ 2 if(l == r){ 3 tree[rt] = C; 4 return ; 5 } 6 int m = (l+r) / 2; 7 if(L <= m) Update( l, m, rt*2, L, C); 8 else Update(m+1, r, rt*2+1, L, C); 9 PushUp(rt); 10 }
4, 查询区间和
查询的规则前面已经解释过一次了。

1 int Query(int l, int r, int rt, int L, int R){// [L,R]为查询区间 2 if(L <= l && r <= R){ // 如果成立则满足查询区间覆盖了当前区间, 直接返回当前区间的值 3 return tree[rt]; 4 } 5 int m = (l+r) / 2; 6 int ret = 0; 7 if(L <= m) ret += Query(l, m, rt*2, L, R); //左边有一部分需要查询的区域。 8 if(m < R) ret += Query(m+1, r, rt*2+1, L, R);//右边有一部分。 9 return ret; 10 }

1 int Query(int l, int r, int rt, int L, int R){ 2 if(L <= l && r <= R){ 3 return tree[rt]; 4 } 5 int m = (l+r) / 2; 6 int ret = 0; 7 if(L <= m) ret += Query(l, m, rt*2, L, R); 8 if(m < R) ret += Query(m+1, r, rt*2+1, L, R); 9 return ret; 10 }
总结
1。首先对于大多数线段树题目来说, 第一步就是建树。 建树用法 Build(1,n,1), [1,n]就是第一个节点所代表的区间长度。
2。在每次更新了点之后,为了保证线段树性质, 一定要去执行PushUP操作,保证线段树的性质不丢失。
3。线段树的精华就是,每一个节点代表着一段区间,这个节点的值,就是他所代表的区间内的值。
4。当底层节点只有5个点的时候, 我们处理线段树时, 需要将他变成8个节点, 如果给9个节点, 那么底层节点必须要有16个节点, 所以为了保证空间足够用,所以需要将空间开大2倍,然后由于每一层的上方都还有 m/2个点(m为该层节点的数目)。
所以空间需要再大两倍, 最终合起来就是4倍。 所以我们需要开 4n 的空间。
HDU-1166 线段树求区间和

1 #include<cstdio> 2 #include<cstring> 3 const int N = 50000+5; 4 int tree[N<<2], a[N]; 5 void PushUp(int rt) { 6 tree[rt] = tree[rt<<1]+tree[rt<<1|1]; 7 } 8 void Build(int l, int r, int rt){ 9 if(l == r) { 10 tree[rt] = a[l]; 11 return ; 12 } 13 int m = l+r >> 1; 14 Build(l, m, rt*2); 15 Build(m+1, r, rt*2+1); 16 PushUp(rt); 17 } 18 void Update(int l, int r, int rt, int L, int C){ 19 if(l == r){ 20 tree[rt] += C; 21 return ; 22 } 23 int m = l+r >> 1; 24 if(L <= m) Update(l, m, rt*2, L, C); 25 else Update(m+1, r, rt*2+1, L, C); 26 PushUp(rt); 27 } 28 int Query(int l, int r, int rt, int L, int R){ 29 if(L <= l && r <= R) return tree[rt]; 30 int ans = 0; 31 int m = l+r >> 1; 32 if(L <= m) ans += Query(l, m, rt*2, L, R); 33 if(m < R) ans += Query(m+1, r, rt*2+1, L, R); 34 return ans; 35 } 36 int main() 37 { 38 int t, n, x, y; 39 char str[100]; 40 scanf("%d", &t); 41 for(int i = 1; i <= t; i++) { 42 printf("Case %d: ", i); 43 int n; 44 scanf("%d", &n); 45 for(int i = 1; i <= n; i++) scanf("%d", &a[i]); 46 Build(1,n,1); 47 while(~scanf("%s", str) && strcmp(str,"End") != 0) { 48 scanf("%d%d", &x, &y); 49 if(str[0] == 'Q') printf("%d ", Query(1, n, 1, x, y)); 50 else if(str[0] == 'A') Update(1, n, 1, x, y); 51 else if(str[0] == 'S') Update(1, n, 1, x, -y); 52 } 53 } 54 return 0; 55 }
HDU-1754 线段树求区间最大值

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N = 200005; 5 int tree[N<<2], a[N]; 6 void PushUp(int rt) { 7 tree[rt] = max(tree[rt<<1], tree[rt<<1|1]); 8 } 9 void Build(int l, int r, int rt) { 10 if(l == r) { 11 tree[rt] = a[l]; 12 return ; 13 } 14 int m = l+r >>1; 15 Build(l, m, rt*2); 16 Build(m+1, r, rt*2+1); 17 PushUp(rt); 18 } 19 void Update(int l, int r, int rt, int L, int C) { 20 if(l == r) { 21 tree[rt] = C; 22 return; 23 } 24 int m = l+r >> 1; 25 if(L <= m) Update(l, m, rt*2, L, C); 26 else Update(m+1, r, rt*2+1, L, C); 27 PushUp(rt); 28 } 29 int Query(int l, int r, int rt, int L, int R) { 30 if(L <= l && r <= R) { 31 return tree[rt]; 32 } 33 int ret = -N, m = l+r >> 1; 34 if(L <= m) ret = max(ret, Query(l, m, rt*2, L, R)); 35 if(m < R) ret = max(ret, Query(m+1, r, rt*2+1, L, R)); 36 return ret; 37 } 38 int main() 39 { 40 int n, m; 41 char str[N]; 42 while(~scanf("%d%d", &n, &m)) { 43 for(int i = 1; i <= n; i++) 44 scanf("%d", &a[i]); 45 Build(1,n,1); 46 int i, j; 47 while(m--) { 48 scanf("%s%d%d", str, &i, &j); 49 if(str[0] == 'Q'){ 50 if(i > j) swap(i, j); 51 printf("%d ", Query(1,n,1,i,j)); 52 } 53 else if(str[0] == 'U') 54 Update(1,n,1,i,j); 55 } 56 } 57 return 0; 58 59 }
区间更新 lazy标记
现在我们突然遇到这样一个题目
这个题目和上面题目不同的地方是更新, 在这个题目中, 他更新数据是成段更新, 上面的题目都是一个点一个点更新, 并且更新的次数不是很少, 我们不可能去像点更新一样, 将这些区域内的点都一个个更新过去。
前面提到过,线段树的每一个节点都代表着一段区间的性质, 所以假如我们需要对于区间 [5,8] 里面的数都加上 10。(基于更新[2,2]后的那个线段树)。

如果我们将一个个点覆盖过去之后, 现在的这课树是这样的。
我们可以发现对节点3来说, 他所管辖的区间[5,8]都是要被更新的区间,并且他增加的指为40,即 区间长度(4) * 修改的值(10)。 我们可以发现,在区域更新的时候, 对于一个节点来说, 如果他所管理的区间 被 要更新的区间 覆盖了, 那我们就提早了知道这一个节点的值。
然后我们引入一个概念, lazy标记, 还是对于开头的情况来说, 如果我们使用了lazy标记之后, 这一课线段树是这样的

在这一颗树上, 我们只修改了2个节点, 同时在节点3处增加了一个 lazy标记, 在这个标记中 lazy = 10。(即整段区间内每一个点都要加上的值)。接下来, 我们如果询问区间[1,8]的和, 我们直接返回节点1就好了。 如果我们询问区间 [3,8] 的和 那么只需要返回 [3,4] + [5,8] 的值。 我们可以看见如果不访问[5,8]的子区间的时候, 我并不会用到里面的值。 在这些时候, 我们并不需要更新里面的值, 更不更新都一样, 不会被访问到。
如果我们现在需要查询 [1,5]的和, 我们只需要将 lazy 标记下推,然后再更新对应的区间就好了。
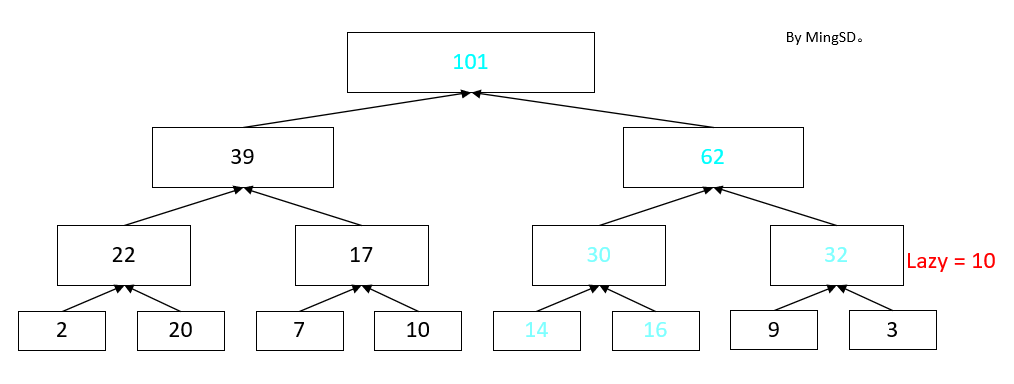
然后我们返回 [1,4] + [5,5] 的值就好了。
总结就是:
lazy标记的含义就是延迟更新,在我们不需要访问区间内部时就保留lazy标记的值,如果需要访问内部的时候,我们要先将lazy标记下推, 因为可能lazy标记还需要继续往下走。
在区域更新的时候,如果 当前区间 被 更新的区间完全覆盖了, 就直接在这个节点加上 区间长度*修改的值, 并且更新这个点的lazy标记。
操作代码:
PushDown --- 将lazy标记下推

1 void PushDown(int rt, int llen, int rlen){ 2 if(lazy[rt]){ 3 lazy[rt*2] += lazy[rt]; 4 lazy[rt*2+1] += lazy[rt]; 5 tree[rt*2] += lazy[rt] * llen; 6 tree[rt*2+1] += lazy[rt] * rlen; 7 lazy[rt] = 0; 8 } 9 }

void Update(int l, int r, int rt, int L, int R, int C){ if(L <= l && r <= R){ tree[rt] += (LL)C*(r-l+1); lazy[rt] += C; return; } int m = (l+r) / 2; PushDown(rt, m-l+1, r-m); if(L <= m) Update(l, m, rt*2, L, R, C); if(m < R) Update(m+1, r, rt*2+1, L, R, C); PushUp(rt); }

1 LL Query(int l, int r, int rt, int L, int R){ 2 if(L <= l && r <= R) return tree[rt]; 3 LL ans = 0; 4 int m = (l+r) / 2; 5 PushDown(rt, m-l+1, r-m); 6 if(L <= m) ans += Query(l, m, rt*2, L, R); 7 if(m < R) ans += Query(m+1, r, rt*2+1, L, R); 8 return ans; 9 }
注意的就是每次对子区间进行修改的时候,我们都需要提前先把lazy标记下推。
所以一开始的那个题目我们就可以做了。

1 #include<cstdio> 2 #define LL long long 3 const int N = 1e5+10; 4 LL tree[N<<2]; 5 LL lazy[N<<2]; 6 int a[N]; 7 void PushUp(int rt){ 8 tree[rt] = tree[rt*2] + tree[rt*2+1]; 9 } 10 void PushDown(int rt, int llen, int rlen){ 11 if(lazy[rt]){ 12 lazy[rt*2] += lazy[rt]; 13 lazy[rt*2+1] += lazy[rt]; 14 tree[rt*2] += lazy[rt] * llen; 15 tree[rt*2+1] += lazy[rt] * rlen; 16 lazy[rt] = 0; 17 } 18 } 19 void Build(int l, int r, int rt){ 20 lazy[rt] = 0; 21 if(l == r){ 22 tree[rt] = a[l]; 23 return ; 24 } 25 int m = (l+r) / 2; 26 Build(l, m, rt*2); 27 Build(m+1, r, rt*2+1); 28 PushUp(rt); 29 } 30 void Update(int l, int r, int rt, int L, int R, int C){ 31 if(L <= l && r <= R){ 32 tree[rt] += (LL)C*(r-l+1); 33 lazy[rt] += C; 34 return; 35 } 36 int m = (l+r) / 2; 37 PushDown(rt, m-l+1, r-m); 38 if(L <= m) Update(l, m, rt*2, L, R, C); 39 if(m < R) Update(m+1, r, rt*2+1, L, R, C); 40 PushUp(rt); 41 } 42 LL Query(int l, int r, int rt, int L, int R){ 43 if(L <= l && r <= R) return tree[rt]; 44 LL ans = 0; 45 int m = (l+r) / 2; 46 PushDown(rt, m-l+1, r-m); 47 if(L <= m) ans += Query(l, m, rt*2, L, R); 48 if(m < R) ans += Query(m+1, r, rt*2+1, L, R); 49 return ans; 50 } 51 int main(){ 52 int n, m, i, j, c; 53 char str[N]; 54 while(~scanf("%d%d", &n, &m)){ 55 for(int i = 1; i <= n; i++) 56 scanf("%d", &a[i]); 57 Build(1, n, 1); 58 while(m--){ 59 scanf("%s", str); 60 if(str[0] == 'Q'){ 61 scanf("%d%d", &i, &j); 62 printf("%lld ", Query(1,n,1,i,j)); 63 } 64 else if(str[0] == 'C'){ 65 scanf("%d%d%d", &i, &j, &c); 66 Update(1,n,1,i,j,c); 67 } 68 } 69 } 70 return 0; 71 }
再来一道

1 #include<cstdio> 2 #define LL long long 3 const int N = 1e5+10; 4 int tree[N<<2]; 5 int lazy[N<<2]; 6 int a[N]; 7 8 void PushUp(int rt){ 9 tree[rt] = tree[rt*2] + tree[rt*2+1]; 10 } 11 void Build(int l, int r, int rt){ 12 lazy[rt] = 0; 13 if(l == r){ 14 tree[rt] = 1; 15 return ; 16 } 17 int m = (l+r) / 2; 18 Build(l, m, rt*2); 19 Build(m+1, r, rt*2+1); 20 PushUp(rt); 21 } 22 void PushDown(int rt, int llen, int rlen){ 23 if(lazy[rt]){ 24 lazy[rt*2] = lazy[rt]; 25 lazy[rt*2+1] = lazy[rt]; 26 tree[rt*2] = lazy[rt] * llen; 27 tree[rt*2+1] = lazy[rt] * rlen; 28 lazy[rt] = 0; 29 } 30 } 31 void Update(int l, int r, int rt, int L, int R, int C){ 32 if(L <= l && r <= R){ 33 tree[rt] = C*(r-l+1); 34 lazy[rt] = C; 35 return; 36 } 37 int m = (l+r) / 2; 38 PushDown(rt, m-l+1, r-m); 39 if(L <= m) Update(l, m, rt*2, L, R, C); 40 if(m < R) Update(m+1, r, rt*2+1, L, R, C); 41 PushUp(rt); 42 } 43 int main(){ 44 int t, n, m, i, j, c; 45 scanf("%d", &t); 46 for(int cas = 1; cas <= t; cas++){ 47 scanf("%d%d", &n, &m); 48 Build(1, n, 1); 49 while(m--){ 50 scanf("%d%d%d", &i, &j, &c); 51 Update(1, n, 1, i, j, c); 52 } 53 printf("Case %d: The total value of the hook is %d. ", cas, tree[1]); 54 } 55 return 0; 56 }
到此关于线段树的查询 单点更新 区域更新都介绍完了。
还有一种特殊的思想是: 线段树求逆序对。
