听课的时候有一道题要单位根反演；
看起来是个轻量级的算法，然后就来学一下
# 引理
定义 $omega_n$ 表示 $n$ 次单位复根，即 $omega_n^n=1$，对于任意正整数 $k$，有
$$ncdot[nmid k]=sum_{i=0}^{n-1}omega_n^{ik}$$
证明只需用到单位复根的性质。
如果 (nmid k)，则 (omega_n^{ik}=1)，
[sum_{i=0}^{n-1}omega_n^{ik}=n
]
此时等比数列的公比不为 (mathbf1)（(nmid k) 的时候公比为 (1)，所以不能用等比数列求和），直接用等比数列求和得到
[sum_{i=0}^{n-1}omega_n^{ik}=frac{1-omega_n^{nk}}{1-omega_n^k}
]
又因为 (omega_n^{nk}=(omega_n^n)^k=1)，所以
[sum_{i=0}^{n-1}omega_n^{ik}=0
]
# 直接推导
求 (n) 次多项式 (f(x)) 的所有 (x^{ik}) 项的系数之和（(kle n)）。形式化的，求
[R=sum_{i=0}^{lfloor frac ni
floor}[x^{ik}]f(x)
]
对式子化简：
[egin{aligned}
R&=sum_{i=0}^{n-1}[kmid i][x^i]f(x)\
&=sum_{i=0}^{n-1}frac 1kBig(sum_{j=0}^{k-1}omega_k^{ij}Big)[x^i]f(x)\
&=sum_{i=0}^{n-1}frac1ksum_{j=0}^{k-1}omega_{k}^{ij}cdot[x^i]f(x)\
&=frac1ksum_{j=0}^{k-1}sum_{i=0}^{n-1}[x^i]f(x)cdot(omega_k^j)^i\
&=frac1ksum_{j=0}^{k-1}f(omega_k^j)
end{aligned}
]
就把 (k) 个单位复根代入式子计算。当然一般来说式子的次数非常高，但是如果式子有比较快速的计算一次的方法，单位根反演就比较有用了。
# DFT推导
另外，还可以用 DFT 理解单位根反演，设 (a_i) 为 ([x^i]f(x))：
[egin{bmatrix}
omega_k^{0 imes 0}&omega_k^{0 imes 1}&cdots&omega_k^{0 imes (n-1)}\
omega_k^{1 imes0}&omega_k^{1 imes1}&cdots&omega_k^{1 imes (n-1)}\
vdots&vdots&ddots&vdots\
omega_k^{(k-1) imes0}&omega_k^{(k-1) imes1}&cdots&omega_k^{(k-1) imes (n-1)}
end{bmatrix}
imes
egin{bmatrix}
a_0\a_1\vdots\a_{n-1}
end{bmatrix}
=
egin{bmatrix}
f(omega_k^{0})\f(omega_k^{1})\vdots\f(omega_k^{k-1})
end{bmatrix}
]
因为单位根 (k) 次一循环，所以可以找到下图所示的规律：
于是可以将矩阵“压缩”成 (k imes k) 的：
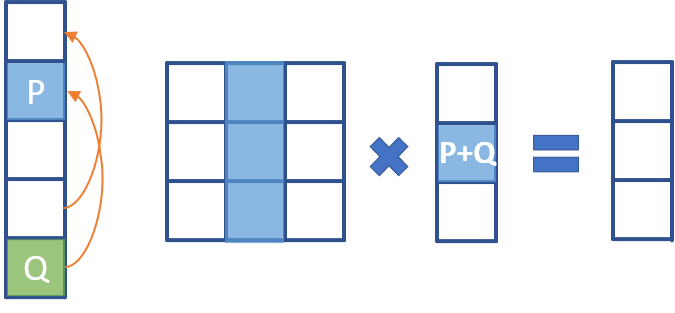
设 (b_t=sum a_{ik+t})，则压缩后的式子就是
[egin{bmatrix}
omega_k^{0 imes 0}&omega_k^{0 imes 1}&cdots&omega_k^{0 imes (k-1)}\
omega_k^{1 imes0}&omega_k^{1 imes1}&cdots&omega_k^{1 imes (k-1)}\
vdots&vdots&ddots&vdots\
omega_k^{(k-1) imes0}&omega_k^{(k-1) imes1}&cdots&omega_k^{(k-1) imes (k-1)}
end{bmatrix}
imes
egin{bmatrix}
b_0\b_1\vdots\b_{k-1}
end{bmatrix}
=
egin{bmatrix}
f(omega_k^{0})\f(omega_k^{1})\vdots\f(omega_k^{k-1})
end{bmatrix}
]
不难发现上式就相当于是对 (b_i) 的矩阵求了一个 DFT，那么我们只需要 IDFT 就可以得到 (b_i) 了。
[b_i=frac1ksum_{t=0}^{k-1}omega_k^{-it}f(omega_k^t)
]
而直接推导求出的 (sum a_{ik}) 的公式则是 IDFT 的一个特例。
# 例题 - 生成树计数加强版(LOJ)
一道不这么板子题的例题
看到不进位加法，而且还是三进制的……只能想到一种做法，拆位。那么只用考虑边权只有 ([0,2]) 的情况。
对于生成树计数，我们有一个很熟悉的算法叫做矩阵树定理。矩阵树定理最基础的应用就是求生成树的总方案数，但是还有一个比较常用的技巧：把矩阵 (M) 中的整数换成其他类型——多项式。
如果存在边 ((u,v)) 的权值为 (w)，则：
M[u][u]+=x^w,M[v][v]+=x^w;
M[u][v]-=x^w,M[v][u]-=x^w;
最后做完矩阵树定理，我们会得到一个次数很高的多项式 (F(x))。(F(x)) 第 (i) 位的系数 (f_i) 表示生成树的边权之和为 (i) 的方案数，而我们要求的答案是
[0 imessum_{i}f_{3i}+1 imessum_{i}f_{3i+1}+2 imessum_{i}f_{3i+2}
]
那么只需要分别求出 (F(x)) 的模 (3) 余 (0,1,2) 的项的系数即可，直接套用单位根反演——做三次行列式，算出 (F(omega_k^0),F(omega_k^1),F(omega_k^2))，然后再 IDFT 就可以了。
/*Lucky_Glass*/
#include<cstdio>
#include<cassert>
#include<cstring>
#include<algorithm>
using namespace std;
const int MOD=1e9+7,VARA=500000003,VARB=541031193,N=105,M=N*N;
#define cint const int &
//(a+bi)^3=1 (mod MOD)
inline int Rint(int &r){
int b=1,c=getchar();r=0;
while(c<'0' || '9'<c) b=c=='-'? -1:b,c=getchar();
while('0'<=c && c<='9') r=(r<<1)+(r<<3)+(c^'0'),c=getchar();
return r*=b;
}
inline int Mul(cint a,cint b){return 1ll*a*b%MOD;}
inline int Pow(cint a,cint b){return b? Mul(Pow(Mul(a,a),b>>1),(b&1)? a:1):1;}
inline int Add(cint a,cint b){return a+b>=MOD? a+b-MOD:a+b;}
inline int Sub(cint a,cint b){return a-b<0? a-b+MOD:a-b;}
#define square(a) Mul(a,a)
const int INV3=Pow(3,MOD-2);
struct NCOMPLEX{
#define cnc const NCOMPLEX &
#define oper(typ) inline friend typ operator
int a,b;
NCOMPLEX(){}
NCOMPLEX(cint A,cint B):a(A),b(B){}
oper(NCOMPLEX) *(cnc A,cnc B){return NCOMPLEX(Sub(Mul(A.a,B.a),Mul(A.b,B.b)),Add(Mul(A.a,B.b),Mul(B.a,A.b)));}
oper(NCOMPLEX) *(cnc A,cint B){return NCOMPLEX(Mul(A.a,B),Mul(A.b,B));}
oper(NCOMPLEX) +(cnc A,cnc B){return NCOMPLEX(Add(A.a,B.a),Add(A.b,B.b));}
oper(NCOMPLEX) -(cnc A,cnc B){return NCOMPLEX(Sub(A.a,B.a),Sub(A.b,B.b));}
oper(NCOMPLEX) -(cnc A){return NCOMPLEX(Sub(0,A.a),Sub(0,A.b));}
inline void operator +=(cnc A){(*this)=(*this)+A;}
inline void operator -=(cnc A){(*this)=(*this)-A;}
inline void operator *=(cnc A){(*this)=(*this)*A;}
inline friend NCOMPLEX inv(cnc A){
return NCOMPLEX(A.a,Sub(0,A.b))
*Pow(Add(square(A.a),square(A.b)),MOD-2);
}
#undef cnc
#undef oper
};
const NCOMPLEX con[3]={NCOMPLEX(1,0),NCOMPLEX(VARA,VARB),NCOMPLEX(VARA,VARB)*NCOMPLEX(VARA,VARB)};
int n,m;
int edg[M][3];
NCOMPLEX mat[N][N];
NCOMPLEX Det(){
NCOMPLEX ans(1,0);
for(int i=1;i<n;i++){
for(int j=i;j<n;j++)
if(mat[j][i].a || mat[j][i].b){
if(i==j) break;
swap(mat[i],mat[j]),ans=-ans;
break;
}
ans=ans*mat[i][i];
NCOMPLEX tmp=inv(mat[i][i]);
for(int j=i+1;j<n;j++){
NCOMPLEX now=mat[j][i]*tmp;
for(int k=i;k<n;k++) mat[j][k]-=now*mat[i][k];
}
}
return ans;
}
inline void IDFT(NCOMPLEX *p){
int i;
NCOMPLEX tmp[3];
tmp[0]=p[0],tmp[1]=p[1],tmp[2]=p[2];
p[0]=tmp[0]+tmp[1]+tmp[2];
p[1]=tmp[0]+tmp[1]*inv(con[1])+tmp[2]*inv(con[2]);
p[2]=tmp[0]+tmp[1]*inv(con[2])+tmp[2]*inv(con[1]);
for(i=0;i<3;++i) p[i]=p[i]*INV3;
}
int Calc(){
NCOMPLEX res[3];
for(int i=0;i<3;i++){
memset(mat,0,sizeof mat);
NCOMPLEX w[3]={con[0],con[i],con[i*2%3]};
for(int j=1;j<=m;j++){
int typ=edg[j][2]%3;
mat[edg[j][0]][edg[j][0]]+=w[typ];
mat[edg[j][1]][edg[j][1]]+=w[typ];
mat[edg[j][0]][edg[j][1]]-=w[typ];
mat[edg[j][1]][edg[j][0]]-=w[typ];
}
res[i]=Det();
}
IDFT(res);
return Add(res[1].a,Add(res[2].a,res[2].a));
}
int main(){
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
Rint(n),Rint(m);
for(int i=1;i<=m;i++)
Rint(edg[i][0]),Rint(edg[i][1]),Rint(edg[i][2]);
int ans=0;
for(int tim=1;;tim=Mul(tim,3)){
ans=Add(ans,Mul(tim,Calc()));
bool exi=false;
for(int i=1;i<=m;i++)
if(edg[i][2]/=3)
exi=true;
if(!exi) break;
}
printf("%d
",ans);
return 0;
}
THE END
Thanks for reading!
[egin{split}
“ &抬头看着星星在唱歌\
&她的呼吸好似对我说\
&她说你要慢慢长大\
&不只为自己活着\
&如果你也听见星星的歌\
&不要哭泣不要再受折磨\
&若你抬起头\
&她就在天空 ”\
——& ext{《星星在唱歌》By 司南}
end{split}
]
> Linked 星星在唱歌-网易云