写在卸载之前
今天在做题的时候突然间看到的
心血来潮 就想着把这些做法好好的总结一下
正式开始
1.欧几里得距离
这个应该是比较好理解的了
对于两个点 ((x_1,y_1),(x_2,y_2))
两个点之间的欧几里得距离也就是二者之间的最短距离
扩展到多维同样如此
2.曼哈顿距离
这个也算是比较好理解
对于这两个点 ((x_1,y_1),(x_2,y_2))
两个点之间的曼哈顿距离就是
扩展到多维
就是这样了
至于具体的操作 我们还是上两道例题详解一下吧
I.【P1661 扩散】
可以发现 过了时间(t)之后两个点扩散会相交 就是(t*2)=两点之间的曼哈顿距离
同时答案具有单调性 所以我们可以二分答案 然后使用上述规则以及并查集判断所有的点是否连通
以前写的代码有些丑
CODE:
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#define int long long
#define IL inline
#define R register
using namespace std;
template<typename T>IL void read(T &A)
{
T x=0,f=1;char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-') f=0;ch=getchar();
}
while(isdigit(ch))
{
x=(x<<1)+(x<<3)+ch-'0';ch=getchar();
}
A=f ? x:-x;
}
struct Node{
int xi,yi;
}e[1001];
int n;
int le,ri,ans;
int fa[1001];
IL int OK(int x,int y)
{
return abs(e[x].xi-e[y].xi)+abs(e[x].yi-e[y].yi);
}
IL int find(int x){return x==fa[x] ? fa[x]:find(fa[x]);}
IL bool check(int now)
{
for(R int i=1;i<=n;++i) fa[i]=i;
for(R int i=1;i<n;++i)
for(R int j=i+1;j<=n;++j)
{
if(OK(i,j)<=(now<<1))
{
int fx=find(i),fy=find(j);
fa[fx]=fy;
}
}
int flag=0;
for(R int i=1;i<=n;++i)
if(find(i)==i) flag++;
return flag==1;
}
signed main()
{
read(n);
for(R int i=1;i<=n;++i)
{
read(e[i].xi);read(e[i].yi);
}
le=0;ri=1000000000;
while(le<=ri)
{
int mid=(le+ri)>>1;
if(check(mid)) {ri=mid-1;ans=mid;}
else le=mid+1;
}
printf("%lld
",ans);
return 0;
}
II.【P5098 [USACO04OPEN]Cave Cows 3】
这个就是真的有些NiuBi了
我们具体分析一下当前的曼哈顿距离
对于两个点((x_1,y_1),(x_2,y_2))
(1.x_1≤x_2,y_1≤y_2)
(2.x_1≥x_2,y_1≥y_2)
(3.x_1≤x_2,y_1≥y_2)
(4.x_1≥x_2,y_1≤y_2)
我们可以发现 答案貌似只跟(x-y,x+y)有关
所以最后的答案就是
CODE:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<cmath>
using namespace std;
int n,ans;
int cdymax,cdymin,wzymax,wzymin;
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cdymax=-2001000;
cdymin=2001000;
wzymax=-2001000;
wzymin=2001000;
cin>>n;
for(int i=1,x,y;i<=n;++i)
{
cin>>x>>y;
cdymax=max(cdymax,x+y);
cdymin=min(cdymin,x+y);
wzymax=max(wzymax,x-y);
wzymin=min(wzymin,x-y);
}
ans=max(cdymax-cdymin,wzymax-wzymin);
cout<<ans<<endl;
return 0;
}
3.切比雪夫距离
比较难的部分来了
两个点((x_1,y_1),(x_2,y_2))的切比雪夫距离
多维空间同样如此
常见的一般模型:
1.在国际象棋棋盘上,国王与王后从一个格子走到另一个格子的最短距离都是切比雪夫距离。
2.若网格图上的一个点只能到周围 88 个点,且到这 88 个点的距离都相同,则该网格图上两点的距离也为切比雪夫距离。
4.平面坐标系转化
主要是曼哈顿坐标系同切比雪夫坐标系之间的转换
首先 我们考虑一下平面上所有到原点曼哈顿距离为(1)的点((x,y))
也就是
也就是
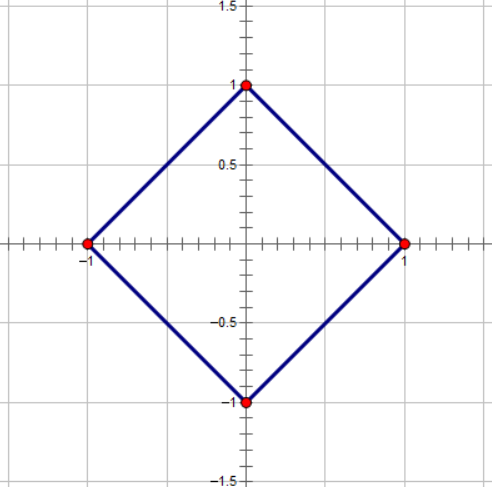
我们再考虑一下平面上所有到原点切比雪夫距离为(1)的点((x,y))
也就是
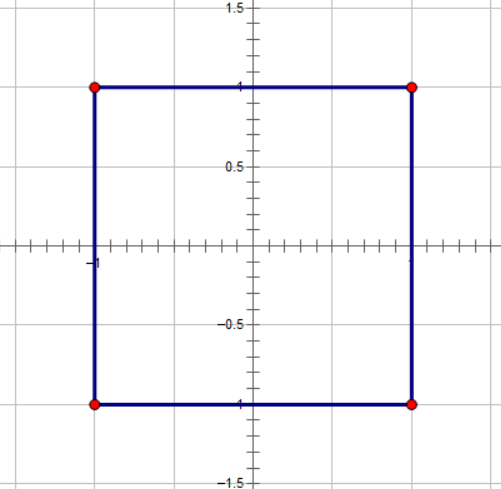
我们可以发现 这两个在平面直角坐标系上的图形居然有着惊人的相似
所以我们不妨探究一下

很多时候 我们都可以通过坐标系的实现二维平面之间点距离问题求解的化简