第六章 非线性优化
1. 理解最小二乘法的含义和处理方式。
2. 理解 Gauss-Newton, Levenburg-Marquadt 等下降策略。
3. 学习 Ceres 库和 g2o 库的基本使用方法。
因为我们的运动方程和观测方程,受各种噪声影响,所以要讨论如何进行准确的状态估计。
6.1 状态估计问题
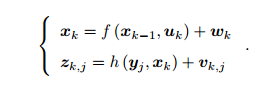 运动方程和观测方程,Xk是位姿,w,v是噪声。
运动方程和观测方程,Xk是位姿,w,v是噪声。
位姿变量 xk 可以由 Tk 或 exp(ξk^) 表达,二者是等价的
由于运动方程在视觉 SLAM 中没有特殊性,我们暂且不讨论它,主要讨论观测方程。假设在 xk 处对路标 yj 进行了一次
观测,对应到图像上的像素位置 zk;j,那么,观测方程可以表示成
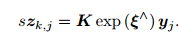 K 为相机内参, s 为像素点的距离
K 为相机内参, s 为像素点的距离
假设两个噪声项 wk; vk;j 满足零均值的高斯分布:
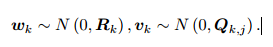
这些噪声的影响下,我们希望通过带噪声的数据 z 和 u,推断位姿 x 和地图 y(以及它们的概率分布),这构成了一个状态
估计问题 。历史上很多人使用扩展滤波器(EKF)求解 ,该方法关心当前时刻的状态估计,近年来普遍使用的非线性优化方法,使用所有时刻采集到的数据进行
状态估计
所有待估计的变量
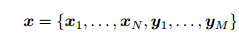
对机器人状态的估计,就是求已知输入数据 u 和观测数据 z 的条件下,计算状态 x 的条件概率分布
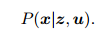
后验概率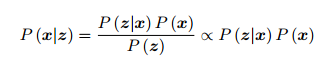 似然
似然
直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下,后验概
率最大化(Maximize a Posterior, MAP),
, 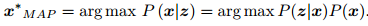
x 的最大似然估计(Maximize Likelihood Estimation, MLE)
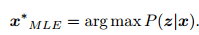
最大似然估计,可以理解成:“在什么样的状态下,最可能产生现在观测到的数据”
最小二乘的引出。
某次观测;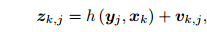
观测数据的条件概率 :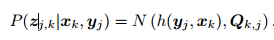 噪声项 vk ∼ N (0; Qk;j)
噪声项 vk ∼ N (0; Qk;j)
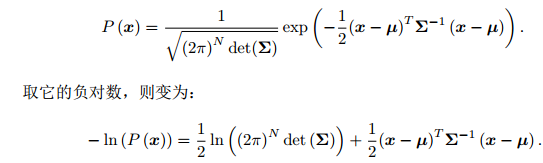
略去第一项,只要最小化右侧的二次型项,就得到了对状态的最大似然估计。
代入 SLAM 的观测模型 即求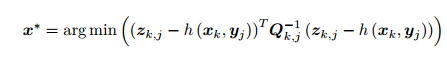

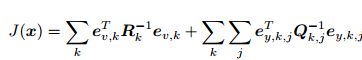
得到了一个总体意义下的最小二乘问题(Least Square Problem)。 我们明白它的最优解等价于状态的最大似然估计 。直观来讲,由于噪声的存在,当我们把估计的轨迹与地图代入 SLAM 的运动、观测方程中时,它们并不会完美的成立。这时候怎么办呢?我们把状态的估计值进行微调,使得整体的误差下降一些。当然这个下降也有限度,它一般会到达一个极小值。这就是一个典型非线性优化的过程
SLAM 中的最小二乘问题具有一些特定的结构:
1.整个问题的目标函数由许多个误差的(加权的)平方和组成 ,且误差项简单
2.整体误差由很多小型误差项之和组成的问题,其增量方程的求解会具有一定的稀疏
性(会在第十讲详细讲解),使得它们在大规模时亦可求解
3.其次,如果使用李代数表示,则该问题是无约束的最小二乘问题
4.我们使用了平方形式(二范数)度量误差 ,直观的
6.2 非线性最小二乘
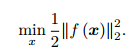 ,f 是任意一个非线性函数 。如果 f 是个数学形式上很简单的函数,那问题也许可以用解析形式来求。令目标函数
,f 是任意一个非线性函数 。如果 f 是个数学形式上很简单的函数,那问题也许可以用解析形式来求。令目标函数
的导数为零,然后求解 x 的最优值,就和一个求二元函数的极值一样:
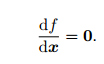
就得到了导数为零处的极值。它们可能是极大、极小或鞍点处的值,只要挨个儿比较它们的函数值大小即可。
对于不方便直接求解的最小二乘问题,我们可以用迭代的方式,从一个初始值出发,不断地更新当前的优化变量,使目标函数下降。 步骤如下
1. 给定某个初始值 x0。
2. 对于第 k 次迭代,寻找一个增量 ∆xk,使得 ∥f (xk + ∆xk)∥2 2 达到极小值。
3. 若 ∆xk 足够小,则停止。
4. 否则,令 xk+1 = xk + ∆xk,返回 2.
直到某个时刻增量非常小,无法再使函数下降。此时算法收敛,目标达到了一个极小,我们完成了寻找极小值的过程。
6.2.1一阶和二阶梯度法、
求解增量最直观的方式是将目标函数在 x 附近进行泰勒展开:
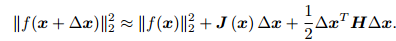
J 是 ∥f(x)∥2 关于 x 的导数(雅可比矩阵), H 则是二阶导数
保留泰勒展开的一阶或二阶项,对应的求解方法则为一阶梯度或二阶梯度法。
保留一阶梯度,那么增量的方向为
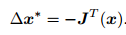 直观意义非常简单,只要我们沿着反向梯度方向前进即可
直观意义非常简单,只要我们沿着反向梯度方向前进即可
还需要该方向上取一个步长 λ,求得最快的下降方式。这种方法被称为最速下降法
保留二阶梯度信息,那么增量方程为 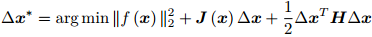
右侧等式关于 ∆x 的导数并令它为零, 得到了增量的解: 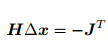 。该方法也称为牛顿法。
。该方法也称为牛顿法。
最速下降法过于贪心,容易走出锯齿路线,反而增加了迭代次数。而牛顿法则需要计算目标函数的 H 矩阵,这在问题规模较大时非常困难,我们通常倾向于避免 H 的计算。所以,接下来我们详细地介绍两类更加实用的方
法:高斯牛顿法和列文伯格——马夸尔特方法。
6.2.2 高斯-牛顿法
Gauss Newton 是最优化算法里面最简单的方法之一。它的思想是将 f(x) 进行一阶的泰勒展开 请注意不是目标函数 f(x)2
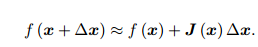 J(x) 为 f(x) 关于 x 的导数
J(x) 为 f(x) 关于 x 的导数
当前的目标是为了寻找下降矢量 ∆x,使得 ∥f (x + ∆x)∥2 达到最小。为了求 ∆x,我们需要解一个线性的最小二乘问题
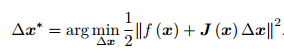
根据极值条件,将上述目标函数对 ∆x 求导,并令导数为零。由于这里考虑的是 ∆x 的导数(而不是 x),我们最后将得到一个线性的方程。
为此,先展开目标函数的平方项

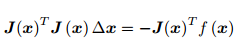 这是一个线性方程组,我们称它为增量方程,
这是一个线性方程组,我们称它为增量方程,
左边定义为H,右边定义为g
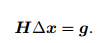 。高斯牛顿法将JTJ近似为牛顿法二阶H矩阵。
。高斯牛顿法将JTJ近似为牛顿法二阶H矩阵。
Gauss-Newton 的算法步骤可以写成:
1. 给定初始值 x0。
2. 对于第 k 次迭代,求出当前的雅可比矩阵 J(xk) 和误差 f(xk)。
3. 求解增量方程: H∆xk = g:
4. 若 ∆xk 足够小,则停止。否则,令 xk+1 = xk + ∆xk,返回 2.
缺点:JTJ可能为奇异矩阵或者病态,算法不收敛
6.2.3 列文伯格 -马夸尔特
给 ∆x 添加一个信赖区域(Trust Region),不能让它太大而使得近似不准确。
根据我们的近似模型跟实际函数之间的差异来确定这个范围:如果差异小,我们就让范围尽可能大;如果差异大,我们就缩小这个近似范围。因此,考虑使用
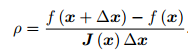 ρ 的分子是实际函数下降的值,分母是近似模型下降的值
ρ 的分子是实际函数下降的值,分母是近似模型下降的值
算法步骤:
1. 给定初始值 x0,以及初始优化半径 µ。
2. 对于第 k 次迭代,求解:
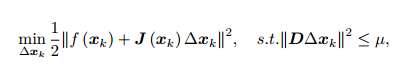 这里 µ 是信赖区域的半径, D 将在后文说明。
这里 µ 是信赖区域的半径, D 将在后文说明。
3. 计算 ρ。
4. 若 ρ > 3 4,则 µ = 2µ;
5. 若 ρ < 1 4,则 µ = 0:5µ;
6. 如果 ρ 大于某阈值,认为近似可行。令 xk+1 = xk + ∆xk。
7. 判断算法是否收敛。如不收敛则返回 2,否则结束。
D 取成单位阵 I,相当于直接把 ∆x 约束在一个球中。
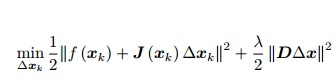 =ζ(∆XK,λ)
=ζ(∆XK,λ)
当参数 λ 比较小时, H 占主要地位,这说明二次近似模型在该范围内是比较好的, L-M 方法更接近于 G-N 法。另一方面,当 λ 比较大时, λI 占据主要地位, L-M更接近于一阶梯度下降法(即最速下降),这说明附近的二次近似不够好。