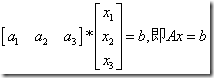开关问题Description
有N个相同的开关,每个开关都与某些开关有着联系,每当你打开或者关闭某个开关的时候,其他的与此开关相关联的开关也会相应地发生变化,即这些相联系的开关的状态如果原来为开就变为关,如果为关就变为开。你的目标是经过若干次开关操作后使得最后N个开关达到一个特定的状态。对于任意一个开关,最多只能进行一次开关操作。你的任务是,计算有多少种可以达到指定状态的方法。(不计开关操作的顺序)Input
输入第一行有一个数K,表示以下有K组测试数据。
每组测试数据的格式如下:
第一行 一个数N(0 < N < 29)
第二行 N个0或者1的数,表示开始时N个开关状态。
第三行 N个0或者1的数,表示操作结束后N个开关的状态。
接下来 每行两个数I J,表示如果操作第 I 个开关,第J个开关的状态也会变化。每组数据以 0 0 结束。Output
如果有可行方法,输出总数,否则输出“Oh,it's impossible~!!” 不包括引号Sample Input
2 3 0 0 0 1 1 1 1 2 1 3 2 1 2 3 3 1 3 2 0 0 3 0 0 0 1 0 1 1 2 2 1 0 0Sample Output
4 Oh,it's impossible~!!Hint
第一组数据的说明:
一共以下四种方法:
操作开关1
操作开关2
操作开关3
操作开关1、2、3 (不记顺序)
某些开关的动作可能影响另一些开关的状态,因此以开关为节点,如果存在这种关系就加入一条有向边(开始我想成对称的了,浪费了很多时间- -),这样就构成了一个图,可以用邻接矩阵表示(但是要转置一下,后面细说)。当某个开关按下时,其自身状态改变,受其影响的开关的状态也改变。
用两个N维向量表示初始状态和结束状态,两者逐个元素异或,就得到了开关状态的变化。
以第一个样例输入为例分析,3个开关,两两相连,初始状态000,最终状态111,开关对应的邻接矩阵为
将对角线的0全部换成1,得矩阵A=
将矩阵每一列想象为一个开关按下后产生的效果(1表示状态翻转,0表示不变),比如,第二列就表示按下第二个开关,则第二个开关的本身状态要改变(这就是把对角线0换成1的原因),受第二个开关影响的开关j状态也要改变,恰好对应邻接矩阵中A[j, 2]=1
把A写成分块矩阵的形式,每一列作为一个子矩阵,则有A=[a1, a2, a3],此处ai均为列
向量,设第i个开关按下次数为xi,xi=0或1(开关按两下和没按是等效的,0/1就够了)
记初始状态b0=[0,0,0],最终状态b1=[1,1,1],则状态变化b=b0^b1=[1,1,1],这里b也是列
向量。目标就是求x1a1 + x2a2 +x3a3 = b的解的个数(此处的加是模2加,也就是异或,下同)
这个方程可以写成
下面就是解这个线性方程组
对增广矩阵[A b]做初等行变换,化成阶梯形(高斯消元法),如果存在[0,0,…,0,1]的行,就是无解;如果存在r行[0,0,…,0,0],就意味着有r个自由变量,因为这里的变量只取0/1,所以有2r个解;如果不存在[0,0,…,0,*],即把最后一行去掉后不存在全0行,则A为满秩矩阵,则方程组有唯一解。
转自:http://www.cnblogs.com/fstang/archive/2013/01/24/2874231.html
本题代码如下:

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 #include<queue> 7 #include<cmath> 8 using namespace std; 9 #define Maxn 40 10 11 int a[Maxn],b[Maxn]; 12 int t[Maxn][Maxn]; 13 14 int n; 15 16 void debug() 17 { 18 for(int i=1;i<=n;i++) 19 { 20 for(int j=1;j<=n+1;j++) 21 { 22 printf("%d ",t[i][j]); 23 } 24 printf(" "); 25 }printf(" "); 26 } 27 28 void init() 29 { 30 scanf("%d",&n); 31 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 32 for(int i=1;i<=n;i++) 33 { 34 int x; 35 scanf("%d",&x); 36 a[i]^=x; 37 } 38 memset(t,0,sizeof(t)); 39 while(1) 40 { 41 int x,y; 42 scanf("%d%d",&x,&y); 43 if(x==0&&y==0) break; 44 // t[x][y]=1; 45 t[y][x]=1; 46 } 47 for(int i=1;i<=n;i++) t[i][i]=1; 48 for(int i=1;i<=n;i++) t[i][n+1]=a[i]; 49 } 50 51 int ffind() 52 { 53 // debug(); 54 int l=1,r=1; 55 while(l<=n&&r<=n) 56 { 57 if(t[l][r]==0) 58 { 59 for(int i=l+1;i<=n;i++) if(t[i][r]==1) 60 { 61 for(int j=r;j<=n+1;j++) 62 { 63 swap(t[i][j],t[l][j]); 64 } 65 break; 66 } 67 } 68 // debug(); 69 if(t[l][r]==0) 70 { 71 r++;continue; 72 } 73 for(int i=l+1;i<=n;i++) if(t[i][r]==1) 74 { 75 for(int j=r;j<=n+1;j++) 76 t[i][j]^=t[l][j]; 77 78 } 79 // printf("%d %d: ",l,r); 80 // debug(); 81 l++,r++; 82 } 83 84 //无解 85 for(int i=l;i<=n;i++) 86 { 87 if (t[i][n+1]!=0) return -1; 88 } 89 return 1<<(n-l+1); 90 } 91 92 int main() 93 { 94 int T; 95 scanf("%d",&T); 96 while(T--) 97 { 98 init(); 99 int ans=ffind(); 100 if(ans==-1) printf("Oh,it's impossible~!! "); 101 else printf("%d ",ans); 102 } 103 return 0; 104 }
2016-09-26 22:09:29
第一道题照例总结:
看了一个高斯消元的总结,代码写得很漂亮,分类很清楚,还有注释,我就是看这个懂了一点点的。。
慢慢看代码就懂了~
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
const int maxn = 105;
int equ, var; // 有equ个方程,var个变元。增广阵行数为equ, 分别为0到equ - 1,列数为var + 1,分别为0到var.
int a[maxn][maxn];
int x[maxn]; // 解集.
bool free_x[maxn]; // 判断是否是不确定的变元.
int free_num;
void Debug(void)
{
int i, j;
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
cout << a[i][j] << " ";
}
cout << endl;
}
cout << endl;
}
inline int gcd(int a, int b)
{
int t;
while (b != 0)
{
t = b;
b = a % b;
a = t;
}
return a;
}
inline int lcm(int a, int b)
{
return a * b / gcd(a, b);
}
// 高斯消元法解方程组(Gauss-Jordan elimination).(-2表示有浮点数解,但无整数解,-1表示无解,0表示唯一解,大于0表示无穷解,并返回自由变元的个数)
int Gauss(void)
{
int i, j, k;
int max_r; // 当前这列绝对值最大的行.
int col; // 当前处理的列.
int ta, tb;
int LCM;
int temp;
int free_x_num;
int free_index;
// 转换为阶梯阵.
col = 0; // 当前处理的列.
// Debug();
for (k = 0; k < equ && col < var; k++, col++)
{ // 枚举当前处理的行.
// 找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)
max_r = k;
for (i = k + 1; i < equ; i++)
{
if (abs(a[i][col]) > abs(a[max_r][col])) max_r = i;
}
if (max_r != k)
{ // 与第k行交换.
for (j = k; j < var + 1; j++) swap(a[k][j], a[max_r][j]);
}
// Debug();
if (a[k][col] == 0)
{ // 说明该col列第k行以下全是0了,则处理当前行的下一列.
k--; continue;
}
for (i = k + 1; i < equ; i++)
{ // 枚举要删去的行.
if (a[i][col] != 0)
{
LCM = lcm(abs(a[i][col]), abs(a[k][col]));
ta = LCM / abs(a[i][col]), tb = LCM / abs(a[k][col]);
if (a[i][col] * a[k][col] < 0) tb = -tb; // 异号的情况是两个数相加.
for (j = col; j < var + 1; j++)
{
a[i][j] = a[i][j] * ta - a[k][j] * tb;
}
}
// Debug();
}
// Debug();
}
Debug();
// 1. 无解的情况: 化简的增广阵中存在(0, 0, ..., a)这样的行(a != 0).
for (i = k; i < equ; i++)
{ // 对于无穷解来说,如果要判断哪些是自由变元,那么初等行变换中的交换就会影响,则要记录交换.
if (a[i][col] != 0) return -1;
}
// 2. 无穷解的情况: 在var * (var + 1)的增广阵中出现(0, 0, ..., 0)这样的行,即说明没有形成严格的上三角阵.
// 且出现的行数即为自由变元的个数.
if (k < var)
{
// 首先,自由变元有var - k个,即不确定的变元至少有var - k个.
for (i = k - 1; i >= 0; i--)
{
// 第i行一定不会是(0, 0, ..., 0)的情况,因为这样的行是在第k行到第equ行.
// 同样,第i行一定不会是(0, 0, ..., a), a != 0的情况,这样的无解的.
free_x_num = 0; // 用于判断该行中的不确定的变元的个数,如果超过1个,则无法求解,它们仍然为不确定的变元.
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && free_x[j]) free_x_num++, free_index = j;
}
if (free_x_num > 1) continue; // 无法求解出确定的变元.
// 说明就只有一个不确定的变元free_index,那么可以求解出该变元,且该变元是确定的.
temp = a[i][var];
for (j = 0; j < var; j++)
{
if (a[i][j] != 0 && j != free_index) temp -= a[i][j] * x[j];
}
x[free_index] = temp / a[i][free_index]; // 求出该变元.
free_x[free_index] = 0; // 该变元是确定的.
}
return var - k; // 自由变元有var - k个.
}
// 3. 唯一解的情况: 在var * (var + 1)的增广阵中形成严格的上三角阵.
// 计算出Xn-1, Xn-2 ... X0.
for (i = var - 1; i >= 0; i--)
{
temp = a[i][var];
for (j = i + 1; j < var; j++)
{
if (a[i][j] != 0) temp -= a[i][j] * x[j];
}
if (temp % a[i][i] != 0) return -2; // 说明有浮点数解,但无整数解.
x[i] = temp / a[i][i];
}
return 0;
}
int main(void)
{
int i, j;
while (scanf("%d %d", &equ, &var) != EOF)
{
memset(a, 0, sizeof(a));
memset(x, 0, sizeof(x));
memset(free_x, 1, sizeof(free_x)); // 一开始全是不确定的变元.
for (i = 0; i < equ; i++)
{
for (j = 0; j < var + 1; j++)
{
scanf("%d", &a[i][j]);
}
}
// Debug();
free_num = Gauss();
if (free_num == -1) printf("无解!
");
else if (free_num == -2) printf("有浮点数解,无整数解!
");
else if (free_num > 0)
{
printf("无穷多解! 自由变元个数为%d
", free_num);
for (i = 0; i < var; i++)
{
if (free_x[i]) printf("x%d 是不确定的
", i + 1);
else printf("x%d: %d
", i + 1, x[i]);
}
}
else
{
for (i = 0; i < var; i++)
{
printf("x%d: %d
", i + 1, x[i]);
}
}
printf("
");
}
return 0;
}
比如我们做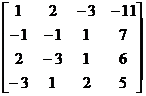 这个矩阵
这个矩阵
我们看一看他的过程(点开看):

1 1 2 -3 -11 2 -1 -1 1 7 3 2 -3 1 6 4 -3 1 2 5 5 6 -3 1 2 5 7 -1 -1 1 7 8 2 -3 1 6 9 1 2 -3 -11 10 11 -3 1 2 5 12 0 -4 1 16 13 2 -3 1 6 14 1 2 -3 -11 15 16 -3 1 2 5 17 0 -4 1 16 18 0 -7 7 28 19 1 2 -3 -11 20 21 -3 1 2 5 22 0 -4 1 16 23 0 -7 7 28 24 0 7 -7 -28 25 26 -3 1 2 5 27 0 -4 1 16 28 0 -7 7 28 29 0 7 -7 -28 30 31 -3 1 2 5 32 0 -7 7 28 33 0 -4 1 16 34 0 7 -7 -28 35 36 -3 1 2 5 37 0 -7 7 28 38 0 0 -21 0 39 0 7 -7 -28 40 41 -3 1 2 5 42 0 -7 7 28 43 0 0 -21 0 44 0 0 0 0 45 46 -3 1 2 5 47 0 -7 7 28 48 0 0 -21 0 49 0 0 0 0 50 51 -3 1 2 5 52 0 -7 7 28 53 0 0 -21 0 54 0 0 0 0 55 56 -3 1 2 5 57 0 -7 7 28 58 0 0 -21 0 59 0 0 0 0 60 61 -3 1 2 5 62 0 -7 7 28 63 0 0 -21 0 64 0 0 0 0 65 66 -3 1 2 5 67 0 -7 7 28 68 0 0 -21 0 69 0 0 0 0 70 71 x1: -3 72 x2: -4 73 x3: 0
总的来说就是:
*目标:梯形矩阵
init:构造增广矩阵
1.把某行这列最大的交换上来
2.把这列下面的都变成0,(利用这行的值进行初等行变换)
3.判断解的类型
涉及到一个概念:矩阵的轶 [上度娘]

感觉就是,独立的行是有用的,不能用前面进行初等行变换而得到的,就是说不会把它系数全部变成0的。
矩阵的轶就是化成阶梯矩阵后系数全0行的行数。
推论1 线性方程组有唯一解的充分必要条件是r(A)=r(A B)=n 。
推论2 线性方程组有无穷多解的充分必要条件是r(A)=r(A B)<n 。
无穷解时还涉及概念 自由未知量
未完待续。。。
2016-09-26 22:09:33