CF559E Gerald and Path

题目链接

没看懂题解，但是大概知道它的思路了，然后自己造了一种实现方式。

首先按照那个点从小到大排序。设 (f_{i,j,t}) 表示考虑了前 (i) 个线段，最靠右的线段为第 (j) 个且方向为 (t)（0左1右），的最大覆盖长度。转移就多考虑一个线段，考虑要不要选它，方向是啥，随便DP一下就好了。

for (int i = 1; i <= n; ++i) {
	memcpy(f[i], f[i - 1], sizeof(f[i]));
	for (int np = 0; np < 2; ++np) {
		for (int j = 0; j < i; ++j) {
			for (int p = 0; p < 2; ++p) {
				int nwp = S[i].p, nwlen = S[i].l;
				int lstp = S[j].p, lstlen = S[j].l;
				int nwr = nwp + (np == 1 ? nwlen : 0);
				int lstr = lstp + (p == 1 ? lstlen : 0);
				int nwl = nwr - nwlen;
				if (lstr > nwr)	continue;
				int res = f[i - 1][j][p];
				if (nwl >= lstr) res += nwlen;
				else	res += nwr - lstr;
				MAX(f[i][i][np], res);
				MAX(ans, res);
			}
		}
	}
} 

然后发现过不了样例。而反例仅有：

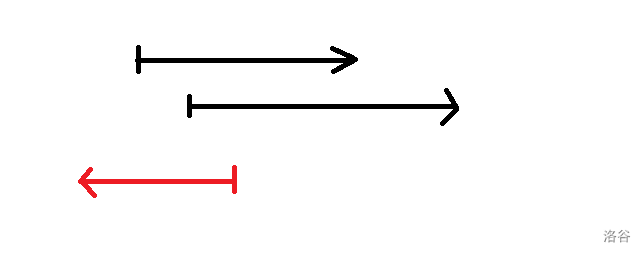
算红色的线的时候它明明能够多覆盖左边的一篇区域，结果我们认为它“无用”，扔掉了它。而这种情况只有 之前线段向右，当前线段向左 才会发生。于是考虑按块转移，将这种情况从这几个线段前直接转移到当前线段。我们只需要知道黑色线段的右端点最大值即可。

有一些细节，各种情况要特判一下。

复杂度：(O(n^3))。

for (int i = 1; i <= n; ++i) {
	memcpy(f[i], f[i - 1], sizeof(f[i]));
	for (int np = 0; np < 2; ++np) {
		for (int j = 0; j < i; ++j) {
			for (int p = 0; p < 2; ++p) {
				int nwp = S[i].p, nwlen = S[i].l;
				int lstp = S[j].p, lstlen = S[j].l;
				int nwr = nwp + (np == 1 ? nwlen : 0);
				int lstr = lstp + (p == 1 ? lstlen : 0);
				int nwl = nwr - nwlen;
				if (lstr > nwr)	continue;
				int res = f[i - 1][j][p];
				if (nwl >= lstr) res += nwlen;
				else	res += nwr - lstr;
				MAX(f[i][i][np], res);
				MAX(ans, res);
			}
		}
	}
	int mxr = -inf, whic = 0;
	for (int j = i - 1; j; --j) {
		int r = S[j].p + S[j].l;
		if (r > mxr)	mxr = r, whic = j;
		if (mxr <= S[i].p)	continue;
		for (int k = j - 1; ~k; --k) {
			for (int t = 0; t < 2; ++t) {
				int lstr = S[k].p + (t == 1 ? S[k].l : 0);
				if (lstr >= S[i].p)	continue;
				int tmp = mxr - max(S[i].p - S[i].l, lstr);
				MAX(f[i][whic][1], f[j - 1][k][t] + tmp);
				MAX(ans, f[i][whic][1]);
			}
		}
	}
}