<数论相关>欧几里得与拓展欧几里得证明及应用

欧几里得算法

欧几里得算法的复杂度为O(log(n))，是一个非常高效的求最大公约数算法。

在这里不证明欧几里得算法的复杂度，有兴趣的可以访问以下链接：http://blog.sina.com.cn/s/blog_62e4e31a0101feo7.html

定义如下：

欧几里德算法是用来求两个正整数最大公约数的算法。是由古希腊数学家欧几里德在其著作《The Elements》中最早描述了这种算法,所以被命名为欧几里德算法。

计算公式为：gcd(a,b) = gcd(b,a mod b)

证明：

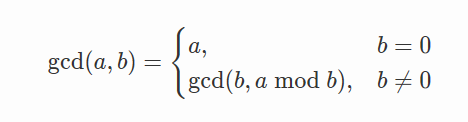
边界情况：gcd(n,0)=n 因为当除数为0时任何数都可以整除0；此时最大公约数为被除数n；

一般情况：设a除以b商为p余数为q 则有 a = b*p + q；

a可以看作是两部分相加根据模数的性质 (x+y)%p = (x%p + y%p) %p 即 a可以整除b*p与q的最大公因数，当然也可以整除b与q的最大公因数

有b与q的最大公因数gcd(b,q)，可知a一定可以整除gcd(b,q)，所以a,b,q都可以整除gcd(b,q)，因此gcd(b,q)可以整除gcd(a,b)；

变化一下形式 q=a-b*p，同理可得gcd(a,b)整除gcd(b,q)；

综上可以得到gcd(a,b)=gcd(b,a%b)

证毕。

拓展欧几里得算法

扩展欧几里德算法可以用来求解形如 ax+by=c的方程的一组整数解（其中a,b,c均为整数）

存在整数解的充分条件是gcd(a,b)|c，即c为a b最大公约数的一个倍数;

求解：

先将等式左右两边同时除以gcd(a,b)，不影响后续计算

即ax+by=1且a与b互质。

由于：

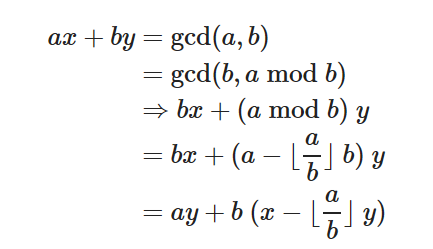
所以x变成了y，y变成了x-[a/b]*y，利用这个关系可以带入递推公式求解。

特殊性：当b=0的时候，a=1，此时x=1，y=0

代码实现：

void Exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) x = 1, y = 0;
    else Exgcd(b, a % b, y, x), y -= a / b * x;
}