【暖*墟】 #树与图# 深度优先遍历入门知识点

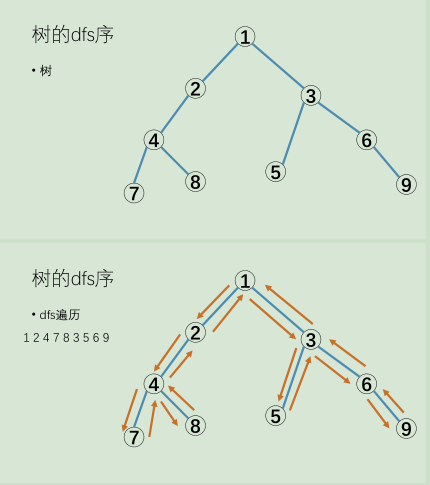
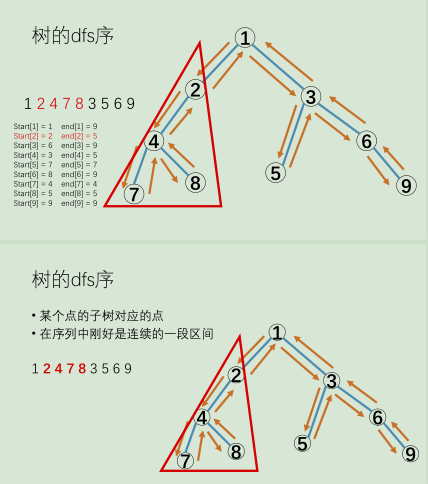
【一. 时间戳（dfn）】

什么是时间戳? 就是每个位置被访问到的次序。

比如说我们对一棵树进行深搜,在深搜中访问的相应次序就被我们称为时间戳。

【二. 树的dfs序】

1.dfs序的作用

维护一系列树上的问题，解决一棵树上的所有后代结点信息的更改和祖先结点有关改变，

通过dfs来记录树的每个顶点的出入时间戳，来控制它子树上的所有结点的状态的更新。

用 L[ i ],R[ i ] 来记录这个祖先结点控制后代结点的区间。

即dfs序的特点就是：每个节点编号x在序列中恰好出现两次。

一棵子树的dfs序就变成了一个区间 [ L[ x ] , R[ x ] ] 。

树的dfs序也用于深搜解决树的前序、中序、后序遍历问题。

把树上的问题转化成了序列上的问题
辅以各种数据结构（ST表、树状数组、线段树）进行运算
子树求和->区间求和

2.dfs序的图解

3.dfs序的代码

void dfs(int x){
    a[++m]=x; //a数组储存dfs序
    v[x]=1; //记录点x被访问过
    for(int i=head[x];i;i=next[i]){
        int y=ver[i]; //取出点的价值
        if(v[y]) continue; //已经到达过
        dfs(y);
    }
    a[++m]=x; //dfs返回到x
}

4.例题：poj3321 Apple Tree

【三. 树的深度、直径和重心】

1.树的深度

已知根节点深度为0。自顶而下统计信息。

若节点x的深度为 d[x] ，则它的子节点y的深度就是 d[y]=d[x]+1 。

结合dfs，可求得每个节点的深度。

void dfs_deep(int x){
    v[x]=1; //记录x点被访问过
    for(int i=head[x];i;i=next[i]){
        int y=ver[i];
        if(v[y]) continue;
        d[y]=d[x]+1; dfs_deep(y);
    }
}

2.树的直径与重心

1）树的直径 即树上最长的简单路径。

在树上任选一点w，求距离w最远的点u，求距离u最远的点v，u到v的距离即为树的直径。

简单证明：

<1> 如果w在直径上，那么u一定是直径的一个端点。

反证：若u不是端点，则从直径另一端点到w再到u的距离比直径更长，与假设矛盾。

<2> 如果w不在直径上，且w到其距最远点u的路径与直径一定有一交点c，

那么由上一个证明可知，u是直径的一个端点。

<3> 如果w到最远点u的路径与直径没有交点，设直径的两端为S与T，

那么(w->u)>(w->c)+(c->T)，推出(w->u)+(S->c)+(w->c)>(S->c)+(c->T)=(S->T)与假设矛盾。

因此w到最远点u的路径与直径必有交点。

S-----------c-----------T

w------u

#include<cstdio>
#include<cstring>
#define N 4200
 
struct node{
    int next;
    int to;
}edge[N];
 
int num_edge,head[N],dis[N],n,a,b,y;
 
int add_edge(int from,int to){
    edge[++num_edge].next=head[from];
    edge[num_edge].to=to;
    head[from]=num_edge;
}
 
int dfs(int x){ //计算树的深度
    for(int i=head[x];i;i=edge[i].next)
        if(!dis[edge[i].to]){
            dis[edge[i].to]=dis[x]+1;
            dfs(edge[i].to);
        }
}
 
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;++i){
        scanf("%d%d",&a,&b);
        add_edge(a,b);
        add_edge(b,a);
    }
    
    dfs(1); //计算树的深度
    for(int i=y=1;i<=n;i++)
        if(dis[i]>dis[y])
            y=i; //寻找与w距离最大的某点u
    memset(dis,0,sizeof(dis));
    
    dfs(y); //以y为根，重新建树
    for(int i=y=1;i<=n;i++)
        if(dis[i]>dis[y])
            y=i; //找到离u最大的v
    printf("%d",dis[y]); //得出树的直径
    
    return 0;
}

View Code

2）树的重心 树上一点，使该点为根的所有子树中最大子树的节点数最少。

一般的树只有一个重心，有些有偶数个节点的树，有两个节点。

法一：简单的两次搜索求出。

分别搜索求出每个结点的子结点数量son[u]、使max{son[u],n-son[u]-1}最小的结点。

实际上这两步操作可以在一次遍历中解决。对结点u的每一个儿子v，递归的处理v，

求出son[v]，然后判断是否是结点数最多的子树，处理完所有子结点后，判断u是否为重心。

struct CenterTree{
    int n,ans,siz,son[maxn];
    void dfs(int u,int pa){
        son[u]=1;
        int res=0;
        for(int i=head[u];i!=-1;i=edges[i].next){
            int v=edges[i].to;
            if(v==pa) continue;
            if(vis[v]) continue;
            dfs(v,u); son[u]+=son[v];
            res=max(res,son[v]-1);
        }
        res=max(res,n-son[u]);
        if(res<siz){ ans=u; siz=res; }
    }
    int getCenter(int x){
        ans=0; siz=INF;
        dfs(x,-1);
        return ans;
    }
}Cent;  //树的重心

View Code

法二：利用推论求出。

随意确定一个根节点，先把无根树转化为有根树，dfs求出所有点的子树的节点个数。

如果有一点满足该点的子树的节点数的二倍 >= 总结点数 (size[u]*2>=n)，

并且该点儿子都满足子树节点数二倍 <= 总结点数 (size[son_u]*2<=n)，就是树的重心。

#include<cstdio>
#define N 42000
 
int n,a,b,next[N],to[N],head[N],num,size[N],father[N],ans;
 
void add(int false_from,int false_to){
    next[++num]=head[false_from];
    to[num]=false_to;
    head[false_from]=num;
}
 
void dfs(int x){
    size[x]=1;
    for(int i=head[x];i;i=next[i])
        if(father[x]!=to[i]){
            father[to[i]]=x;
            dfs(to[i]);
            size[x]+=size[to[i]];
        }
    if(size[x]*2>=n&&!ans)
        ans=x;
}
 
int main(){
    scanf("%d",&n);
    for(int i=1;i<n;++i){
        scanf("%d%d",&a,&b);
        add(a,b); add(b,a);
    }
    dfs(1);
    printf("%d",ans);
    return 0;
}

View Code

【四. 图的连通块划分】

1.连通块的定义

连通块（连通图）：无向图 G 中，若从顶点 i 到 j 有路径相连，则 i、j 是连通的。

如果 G 是有向图，那么连接 i 和 j 的路径中所有的边都必须同向。

如果图中任意两点都是连通的，那么图被称作连通图（或连通块）。

如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。

2.求图中连通块的个数

深搜法：

void dfs_num(int x){
    v[x]=cnt; //记录x点属于的连通块的编号
    for(int i=head[x];i;i=next[i]){
        int y=ver[i];
        if(v[y]) continue; //已经找到归属的连通块
        dfs_num(y);
    }
}
 
//在主程序 int main() 中：
for(int i=1;i<=n;i++){
    if(!v[i]){
        cnt++; //无向图中包含连通块的个数
        dfs_num(i);
    }
}

并查集法：

#include <stdio.h>
#include <vector>
using namespace std;
 
const int maxn = 100010;
vector<int> G[maxn]; // 邻接表存储图
 
bool isRoot[maxn] = {false}; // 标记是否访问
int pre[maxn];
 
int Find(int x) {
    int r = x;
    while(x != pre[x])  x = pre[x];
    //↑↑路径压缩:此时x已经是老大
    int j; while(r != pre[r]) {
        j = r;
        r = pre[r];
        pre[j] = x;
    }
    return x;
}
 
void Union(int a, int b) {
    int preA = Find(a);
    int preB = Find(b);
    if(preA != preB) pre[preA] = preB;
}
 
int calculateBlockNum(int n) {
    int block = 0;
    for(int i = 1; i <= n; i++) // 枚举所有顶点
        isRoot[Find(i)] = true;// 这样同样的数字只计算一次
    for(int i = 1; i <= n; i++)
        block += isRoot[i]; //true当1用，false当0用
    return block;
}
 
void init(int n) {
    for(int i = 1; i <= n; i++)
        pre[i] = i;
}
 
int main() {
    int n, a, b; scanf("%d", &n);
    init(n); // 很重要很重要！
    for(int i = 1; i < n; i++) { // n - 1条边
        scanf("%d%d", &a, &b);
        G[a].push_back(b);
        G[b].push_back(a);
        Union(a,b); // 合并顶点a,b所在的集合
    }
    int block = calculateBlockNum(n);
    printf("%d
",block);
}

View Code

在输入边的两个顶点时进行合并+路径压缩，统计pre数组中的元素有多少个不同值即可，

为了统计，用到标记数组，这里没有统计每个块中的元素数目，所以用布尔型的数组即可。

——时间划过风的轨迹，那个少年，还在等你。