目录
1.堆的引出
优先队列可以处理许多问题,例如系统动态地选择优先级最高的任务进行执行;在N个元素中选出前M个元素。。。而用堆来实现优先队列有着巨大的优势,如下图所示。

2.二叉堆
2.1定义
以最大堆为例。

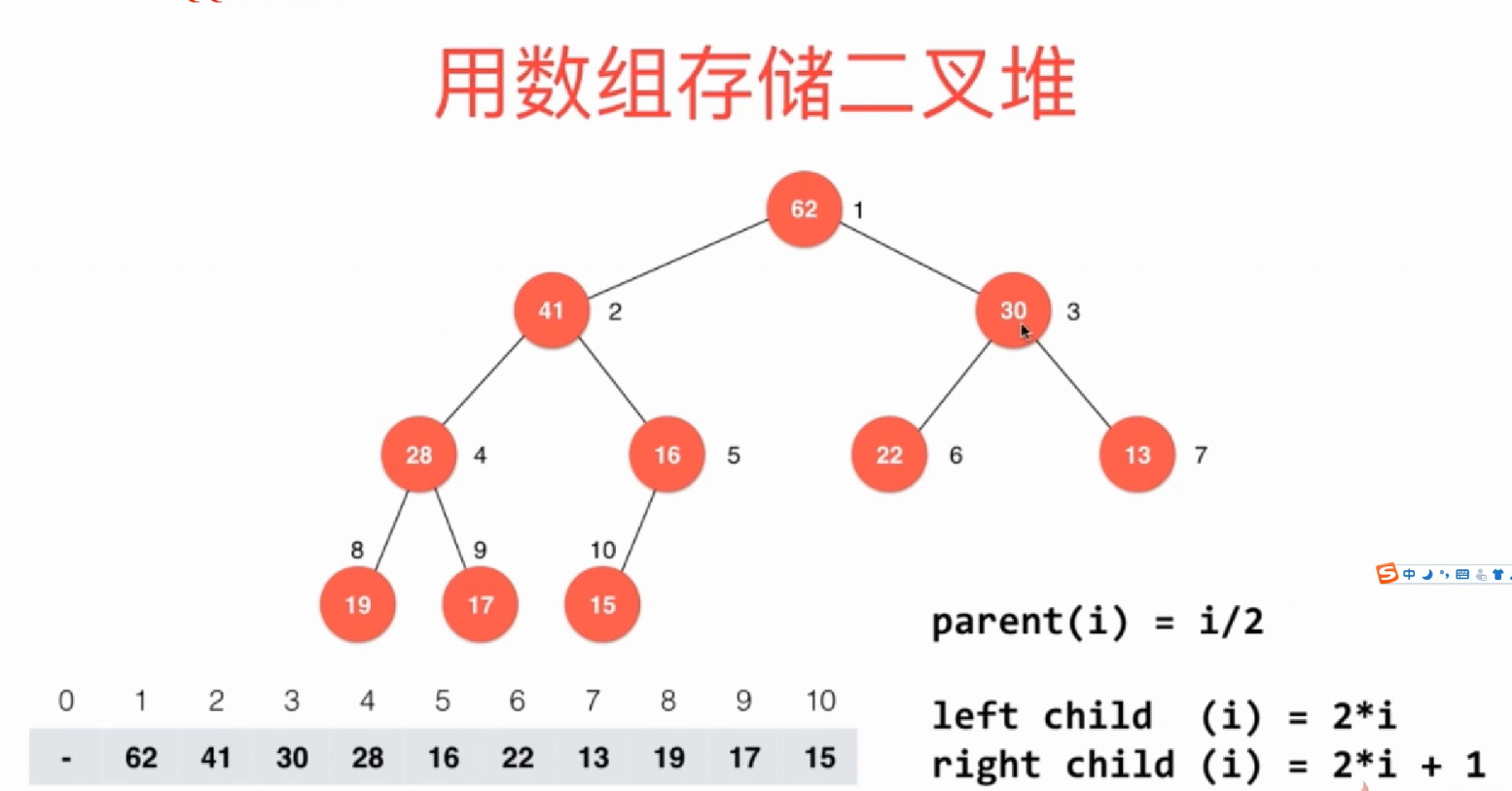
2.2存储
用一个数组来存储二叉堆。(注:从下标为1开始存储)
3.堆操作
3.1insert
思路:首先将要插入的数据放到数组的最后面,然后进行向上调整操作。在shiftUp函数中,首先根据二叉堆的性质,找到第一个可能被破坏二叉树性质的节点(count/2,count为当前节点下标),即当前插入节点的父亲节点。若当前的节点的父节点比当前节点值小,则交换当前节点与父节点的值,直到当前节点小于父节点或者当前节点的父节点为根节点。
void insert(T num)
{
assert(count + 1 < capacity);
data[count + 1] = num;
count++;
shiftUp(count);
}
void shiftUp(int count)
{
while (count > 1 && data[count/2] < data[count])
{
swap(data[count / 2], data[count]);
count /= 2;
}
}
// 将 ShiftUp函数 使用类似插入排序算法的方式进行优化
void shiftUp(int k){
T e = data[k];
while( k > 1 && data[k/2] < e ){
//swap( data[k/2], data[k] );
data[k] = data[k/2];
k /= 2;
}
data[k] = e;
}
3.2extractMax
思路:根据最大堆的性质,最大值保存在下标为1的位置上,取出后将最后一个元素放到根节点位置上,进行向下调整。在shiftDown函数中,选出当前节点左右孩子节点的最大值,若比当前节点位置大,则将它俩进行交换,接着将当前节点变为交换后的节点,不断循环,直到当前节点比其左右孩子节点值都大或者当前节点的孩子节点为数组末尾。
T extractMax()
{
T ret = data[1];
data[1] = data[count];
count--;
shiftDown(0);
return ret;
}
void shiftDown(int k)
{
while ( 2*k <= count )
{
int tmp = 2 * k; //选出左右孩子较大的下标
if (tmp+1 <= count && data[tmp+1] > data[tmp])
{
tmp++;
}
if (data[k] > data[tmp])
break;
swap(data[k], data[tmp]);
k = tmp;
}
}
// 将 ShiftDown函数 使用类似插入排序算法的方式进行优化
void shiftDown(int k)
{
T e = data[k];
while( 2*k <= count ){
int j = 2*k;
if( j+1 <= count && data[j+1] > data[j] ) j ++;
if( e >= data[j] ) break;
//swap( data[k] , data[j] );
data[k] = data[j];
k = j;
}
data[k] = e;
}
3.3其他操作
// 堆中的元素个数
int size()
{
return count;
}
// 堆是否为空
bool isEmpty()
{
return count == 0;
}
// 获取最大堆中的堆顶元素
T getMax()
{
assert( count > 0 );
return data[1];
}
4.堆的创建
4.1方法一:将n个元素依次插入到堆中
// 将所有的元素依次添加到堆中
// 时间复杂度为O(nlogn)
MaxHeap<T> maxheap = MaxHeap<T>(n);
for( int i = 0 ; i < n ; i ++ )
maxheap.insert(arr[i]);
4.2方法二:Heapify(将数组直接复制过来,然后直接建堆)
// 通过一个给定数组创建一个最大堆
// 时间复杂度为O(n)
MaxHeap(Item arr[], int n)
{
data = new Item[n+1];
capacity = n;
//注:堆的存储数组下标是从1开始的
for( int i = 0 ; i < n ; i ++ )
data[i+1] = arr[i];
count = n;
//从后向前找非叶子节点,然后向下调整
for( int i = count/2 ; i >= 1 ; i -- )
shiftDown(i);
}
5.堆排序
5.1heapSort1
根据4.1节方法一,可以很快写出如下堆排序代码。
// heapSort1, 将所有的元素依次添加到堆中, 在将所有元素从堆中依次取出来, 即完成了排序
// 无论是创建堆的过程, 还是从堆中依次取出元素的过程, 时间复杂度均为O(nlogn)
// 整个堆排序的整体时间复杂度为O(nlogn)
template<typename T>
void heapSort1(T arr[], int n)
{
MaxHeap<T> maxheap = MaxHeap<T>(n);
for( int i = 0 ; i < n ; i ++ )
maxheap.insert(arr[i]);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
5.2heapSort2
根据4.2节方法二,可以很快写出如下堆排序代码。
// heapSort2, 借助我们的heapify过程创建堆
// 此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn)
// 堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优
template<typename T>
void heapSort2(T arr[], int n)
{
MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
for( int i = n-1 ; i >= 0 ; i-- )
arr[i] = maxheap.extractMax();
}
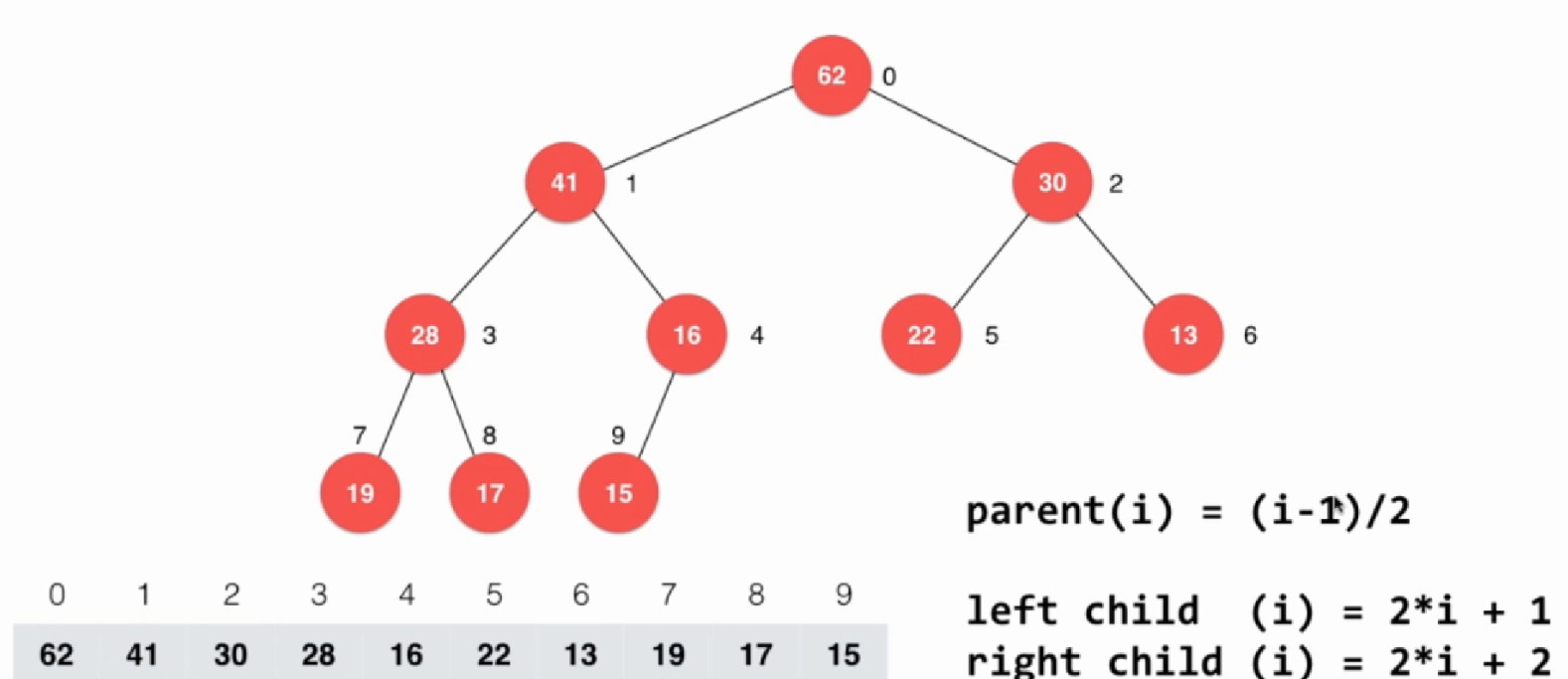
5.3heapSort3(优化,不需要复制元素,直接在原来的数组上原地建堆)
以上两种都需要额外开一个数组来保存要建立的二叉堆,其实可以在原来数组上直接创建堆。由于数组下标是从0开始,所以对应的性质发生了一点改变。
// 原始的shiftDown过程
template<typename T>
void __shiftDown(T arr[], int n, int k){
while( 2*k+1 < n )
{
int j = 2*k+1;
if( j+1 < n && arr[j+1] > arr[j] )
j += 1;
if( arr[k] >= arr[j] )break;
swap( arr[k] , arr[j] );
k = j;
}
}
// 优化的shiftDown过程, 使用赋值的方式取代不断的swap,
// 该优化思想和我们之前对插入排序进行优化的思路是一致的
template<typename T>
void __shiftDown2(T arr[], int n, int k){
T e = arr[k];
while( 2*k+1 < n ){
int j = 2*k+1;
if( j+1 < n && arr[j+1] > arr[j] )
j += 1;
if( e >= arr[j] ) break;
arr[k] = arr[j];
k = j;
}
arr[k] = e;
}
// 不使用一个额外的最大堆, 直接在原数组上进行原地的堆排序
template<typename T>
void heapSort(T arr[], int n)
{
// 注意,此时我们的堆是从0开始索引的
// 从(最后一个元素的索引-1)/2开始
// 最后一个元素的索引 = n-1
for( int i = (n-1-1)/2 ; i >= 0 ; i -- )
__shiftDown2(arr, n, i);
for( int i = n-1; i > 0 ; i-- )
{
swap( arr[0] , arr[i] );
__shiftDown2(arr, i, 0);
}
}
6.索引堆
6.1索引堆的引出
上述介绍的是普通堆的一系列实现,而普通堆存在一系列的局限性:
1.排序前后数组中元素互换位置,若元素结构很复杂,那么交换元素这个操作开销较大
2.若把元素值作为进程的优先级数,下标作为进程号,建成堆以后,进程号与优先级就不一一对应了,若此时想改变原先1号进程的优先级,那只能遍历整个数组了
索引堆将引入另外一个数组,数组中存储索引,以此用来代表堆,而原先数组中的元素保持不变。

6.2初实现
// 最大索引堆
template<typename Item>
class IndexMaxHeap{
private:
Item *data; // 最大索引堆中的数据
int *indexes; // 最大索引堆中的索引
int count;
int capacity;
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftUp( int k )
{
while( k > 1 && data[indexes[k/2]] < data[indexes[k]] )
{
swap( indexes[k/2] , indexes[k] );
k /= 2;
}
}
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftDown( int k ){
while( 2*k <= count ){
int j = 2*k;
if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
j += 1;
if( data[indexes[k]] >= data[indexes[j]] )
break;
swap( indexes[k] , indexes[j] );
k = j;
}
}
public:
// 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
IndexMaxHeap(int capacity){
data = new Item[capacity+1];
indexes = new int[capacity+1];
count = 0;
this->capacity = capacity;
}
~IndexMaxHeap(){
delete[] data;
delete[] indexes;
}
// 返回索引堆中的元素个数
int size(){
return count;
}
// 返回一个布尔值, 表示索引堆中是否为空
bool isEmpty(){
return count == 0;
}
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
void insert(int i, Item item){
assert( count + 1 <= capacity );
assert( i + 1 >= 1 && i + 1 <= capacity );
i += 1;
data[i] = item;
indexes[count+1] = i;
count++;
shiftUp(count);
}
// 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
Item extractMax(){
assert( count > 0 );
Item ret = data[indexes[1]];
swap( indexes[1] , indexes[count] );
count--;
shiftDown(1);
return ret;
}
// 从最大索引堆中取出堆顶元素的索引
int extractMaxIndex(){
assert( count > 0 );
int ret = indexes[1] - 1;
swap( indexes[1] , indexes[count] );
count--;
shiftDown(1);
return ret;
}
// 获取最大索引堆中的堆顶元素
Item getMax(){
assert( count > 0 );
return data[indexes[1]];
}
// 获取最大索引堆中的堆顶元素的索引
int getMaxIndex(){
assert( count > 0 );
return indexes[1]-1;
}
// 获取最大索引堆中索引为i的元素
Item getItem( int i ){
assert( i + 1 >= 1 && i + 1 <= capacity );
return data[i+1];
}
// 将最大索引堆中下标为i的元素修改为newItem
void change( int i , Item newItem ){
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
for( int j = 1 ; j <= count ; j ++ )
if( indexes[j] == i ){
shiftUp(j);
shiftDown(j);
return;
}
}
};
6.3优化
上一节中在change()函数中,查找下标为i在索引数组中的位置使用了遍历的方式,可以引入反向数组,当要找下标i在索引数组中的位置时就可以直接查看reverse[i]的值。

// 最大索引堆
template<typename Item>
class IndexMaxHeap{
private:
Item *data; // 最大索引堆中的数据
int *indexes; // 最大索引堆中的索引, indexes[x] = i 表示索引i在x的位置
int *reverse; // 最大索引堆中的反向索引, reverse[i] = x 表示索引i在x的位置
int count;
int capacity;
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftUp( int k ){
while( k > 1 && data[indexes[k/2]] < data[indexes[k]] ){
swap( indexes[k/2] , indexes[k] );
reverse[indexes[k/2]] = k/2;
reverse[indexes[k]] = k;
k /= 2;
}
}
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
void shiftDown( int k ){
while( 2*k <= count ){
int j = 2*k;
if( j + 1 <= count && data[indexes[j+1]] > data[indexes[j]] )
j += 1;
if( data[indexes[k]] >= data[indexes[j]] )
break;
swap( indexes[k] , indexes[j] );
reverse[indexes[k]] = k;
reverse[indexes[j]] = j;
k = j;
}
}
public:
// 构造函数, 构造一个空的索引堆, 可容纳capacity个元素
IndexMaxHeap(int capacity){
data = new Item[capacity+1];
indexes = new int[capacity+1];
reverse = new int[capacity+1];
for( int i = 0 ; i <= capacity ; i ++ )
reverse[i] = 0;
count = 0;
this->capacity = capacity;
}
~IndexMaxHeap(){
delete[] data;
delete[] indexes;
delete[] reverse;
}
// 返回索引堆中的元素个数
int size(){
return count;
}
// 返回一个布尔值, 表示索引堆中是否为空
bool isEmpty(){
return count == 0;
}
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
void insert(int i, Item item){
assert( count + 1 <= capacity );
assert( i + 1 >= 1 && i + 1 <= capacity );
// 再插入一个新元素前,还需要保证索引i所在的位置是没有元素的。
assert( !contain(i) );
i += 1;
data[i] = item;
indexes[count+1] = i;
reverse[i] = count+1;
count++;
shiftUp(count);
}
// 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
Item extractMax(){
assert( count > 0 );
Item ret = data[indexes[1]];
swap( indexes[1] , indexes[count] );
reverse[indexes[count]] = 0;
count--;
if(count){
reverse[indexes[1]] = 1;
shiftDown(1);
}
return ret;
}
// 从最大索引堆中取出堆顶元素的索引
int extractMaxIndex(){
assert( count > 0 );
int ret = indexes[1] - 1;
swap( indexes[1] , indexes[count] );
reverse[indexes[count]] = 0;
count--;
if(count) {
reverse[indexes[1]] = 1;
shiftDown(1);
}
return ret;
}
// 获取最大索引堆中的堆顶元素
Item getMax(){
assert( count > 0 );
return data[indexes[1]];
}
// 获取最大索引堆中的堆顶元素的索引
int getMaxIndex(){
assert( count > 0 );
return indexes[1]-1;
}
// 看索引i所在的位置是否存在元素
bool contain( int i ){
assert( i + 1 >= 1 && i + 1 <= capacity );
return reverse[i+1] != 0;
}
// 获取最大索引堆中索引为i的元素
Item getItem( int i ){
assert( contain(i) );
return data[i+1];
}
// 将最大索引堆中索引为i的元素修改为newItem
void change( int i , Item newItem ){
assert( contain(i) );
i += 1;
data[i] = newItem;
// 找到indexes[j] = i, j表示data[i]在堆中的位置
// 之后shiftUp(j), 再shiftDown(j)
// for( int j = 1 ; j <= count ; j ++ )
// if( indexes[j] == i ){
// shiftUp(j);
// shiftDown(j);
// return;
// }
// 有了 reverse 之后,
// 我们可以非常简单的通过reverse直接定位索引i在indexes中的位置
shiftUp( reverse[i] );
shiftDown( reverse[i] );
}
};