考虑什么样的 2-染色方式是符合题目要求的,首先蓝、黄颜色所形成的连通块个数必须 (le 2),否则一定不合法,而显然如果两种颜色连通块个数都为 (1) 也不合法,以蓝色连通块个数为 (1),黄色连通块个数为 (2) 为例,稍微画个图即可发现合法的染色方式都如下图所示:
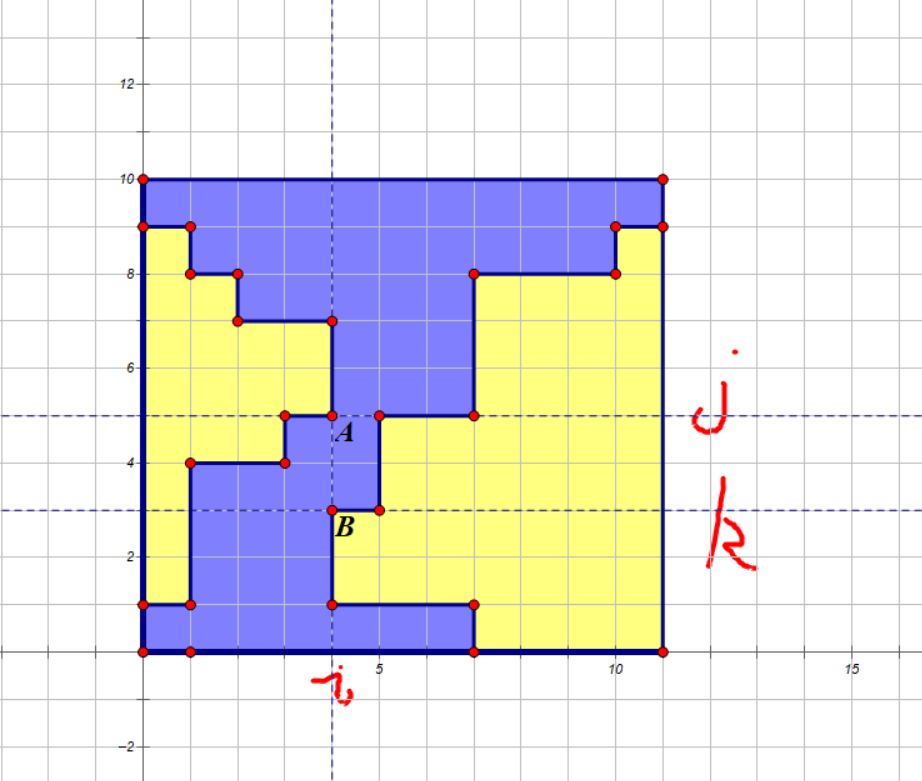
也就是说存在一个分割点 (i),使得第一个连通块全部在第 (i) 列左侧,第二个连通块全部在第 (i) 列右侧,那么显然两个连通块与第 (i) 列的交点分别是一段不相交区间 ((l_1,r_1),(l_2,r_2)),我们假设第一个连通块的区间在第二个连通块的区间的上方,也就是如图所示的情况,那么我们假设 (j=r_1,k=l_2)(当然如果 (j=k) 蓝色连通块会被一分为二,也就是蓝色、黄色连通块个数都为 (2) 的情况),那么显然第一个连通块与直线 (x=i) 的交中最下方的点的坐标就是 ((j,i))(即图中的点 A),第二个连通块与直线 (x=i) 的交中最上方的点就是 ((k,i))(即图中的点 B)。接下来考虑怎样计算方案数,隔板法是肯定没问题的,不过这里有一种更简便的理解方式,以计算 (A) 左上角的方案数为例,它等价于从最左上角的点走到 (A) 的方案数,但由于 (A) 是这段区间中最下方的点,因此最后一步必须是向下走的,因此左上角的方案数就是从最左上角的点走到 (A) 上方的点的方案数,另外四块也同理,如图所示:
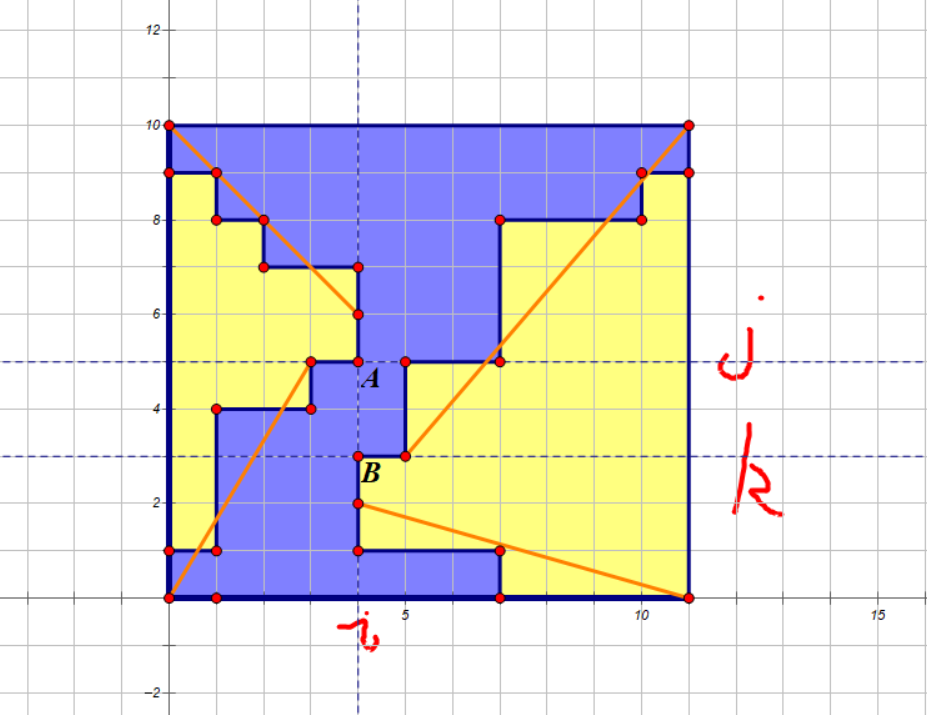
暴力枚举是 (n^2m) 的,通过前缀和优化可以做到 (nm)。对于 ((l_1,r_1)) 在 ((l_2,r_2)) 下方的情况只需乘个 (2) 即可,因为所有 ((l_1,r_1)) 在 ((l_2,r_2)) 上方的情况把它上下翻转都能够得到 ((l_1,r_1)) 在 ((l_2,r_2)) 下方的情况,因此它们构成了一个双射。对于蓝色连通块个数为 (2),黄色连通块个数为 (1) 的情况其实很 simple,只需做整个网络关于 (y=x) 对称的图形即可,但是这样蓝色、黄色连通块个数都是 (2) 的情况会被算重,因此第二次计算的时候需要强制令 (k-jge 1)。
时间复杂度 (mathcal O(nm))
const int MAXN=1<<12;
const int MOD=998244353;
int n,m,fac[MAXN+5],ifac[MAXN+5],ans=0;
void init_fac(int n){
for(int i=(fac[0]=ifac[0]=ifac[1]=1)+1;i<=n;i++) ifac[i]=1ll*ifac[MOD%i]*(MOD-MOD/i)%MOD;
for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%MOD,ifac[i]=1ll*ifac[i-1]*ifac[i]%MOD;
}
int ways(int x,int y){return 1ll*fac[x+y]*ifac[x]%MOD*ifac[y]%MOD;}
int main(){
scanf("%d%d",&n,&m);init_fac(MAXN);
for(int i=1;i<=m-1;i++){
int sum=0;
for(int j=1;j<=n-1;j++){
sum=(sum+1ll*ways(i,j-1)*ways(i-1,n-j))%MOD;
ans=(ans+1ll*sum*ways(m-i-1,j)%MOD*ways(m-i,n-j-1))%MOD;
}
} n^=m^=n^=m;
for(int i=1;i<=m-1;i++){
int sum=0;
for(int j=1;j<=n-1;j++){
ans=(ans+1ll*sum*ways(m-i-1,j)%MOD*ways(m-i,n-j-1))%MOD;
sum=(sum+1ll*ways(i,j-1)*ways(i-1,n-j))%MOD;
}
} printf("%d
",(ans<<1)%MOD);
return 0;
}