差分约束体系
- 有若干个不等式xi<=xj+k(或经过移项可以表示成这个形式)
- 求xt-xs的最大值或最小值。
算法思想
- 考虑对于任意不等式xi<=xj+k,我们将它与最短路中的边类比。
- 在最短路中如果有一条边(u,v),当dis[u]+cost<dis[v]时我们要更新dis[v],使得dis[v]=dis[u]+cost(u,v)
- 实际上最终的dis一定满足任意边(u,v),dis[v]<=dis[u]+cost,并且任意一个非起点的x有一条边使得dis[x]=dis[y]+cost(x,y)。
- 有向图中的dis和不等式中的x实际上是一样的。如果对于不等式xi<=xj+k,由j向i连一条边权为k的边,那么最终的有向图的dis,在最短路算法后满足了dis[v]<=dis[u]+cost(也就是最紧的约束条件),就相当于所有的x满足了xi<=xj+k的约数条件。
- 并且由于我们走的是最短路,实际上可以看作每一次都走不等式的上限k,所以最后的dis[i]即为x[i]-x[s](s是最短路起点)的最大值。
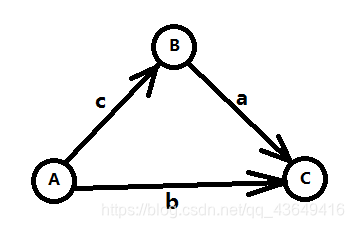
实现
- 任意不等式xi<=xj+k,连一条j到i的边权为k的边。
- 跑s的单源最短路,dis[i]即为x[i]-x[s](s是最短路起点)的最大值。
最小值怎么算?
- 将边依旧按照上面连。求x[t]-x[s]的最小值,等价于求x[s]-x[t]的最大值,跑起点为t的单源最短路。再求个相反数。
- 任意不等式xi>=xj+k,连一条j到i的边权为k的边。然后跑起点为s的最长路(边权取反后跑最短路)。意义与求最大类似。
- 以上两个做法的相对于求最大值得改变,本质分别是边方向取反和边权取反。
- 两个做法的源点也是相反的,所以我们可以分别对所有i求x[i]-x[s]的最小值,或对所有i求x[t]-x[i]的最小值。
无解、有解、无限解
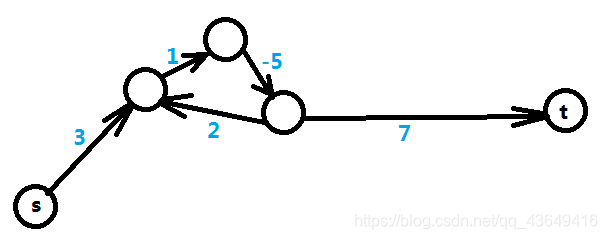
- 负环说明最大值可以趋近无穷大,最小值可以趋近于无穷小,就相当于无解的情况。
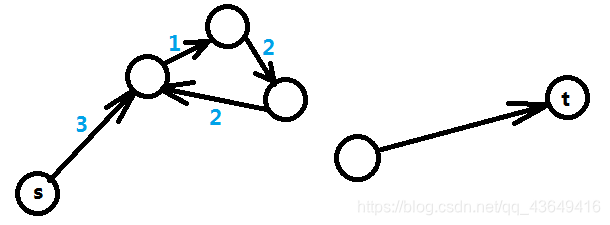
- s和t之间没有路径,即s和t没有限制关系,自然是无限解。
图片来源/参考博客:
https://blog.csdn.net/whereisherofrom/article/details/78922648#commentBox