2D-2D:对极几何
当相机为单目时,我们只知道 2D 的像素坐标,因而问题是根据两组 2D 点估计运动。
对极约束
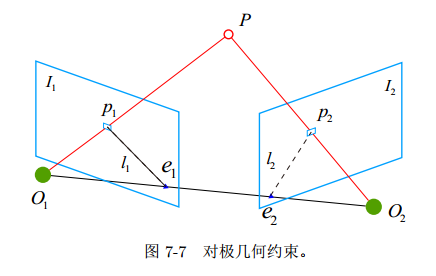
设 P 的空间位置为: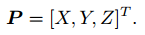
两个像素点 p1; p2 的像素位置为:
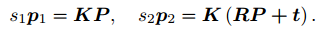
把上式写成在乘以非零常数下成立的( upto a scale)等式:
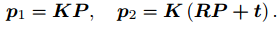
取:
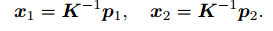
这里的 x1; x2 是两个像素点的归一化平面上的坐标。代入上式,得:
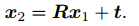
两边同时左乘 t^。

然后,两侧同时左乘 xT 2 :
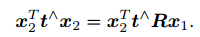
t^x2 是一个与 t 和 x2 都垂直的向量。把它再和 x2 做内积时,将得到 0。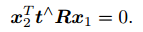
代入 p1; p2,有:
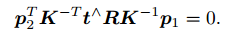
这两个式子都称为对极约束
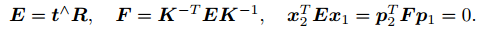
基础矩阵( Fundamental Matrix) F 和本质矩阵( Essential Matrix) E。
于是,相机位姿估计问题变为以下两步:
1. 根据配对点的像素位置,求出 E 或者 F;
2. 根据 E 或者 F,求出 R; t。由于 E 和 F 只相差了相机内参,而内参在 SLAM 中通常是已知的,所以实践当中往往使用形式更简单的 E。
本质矩阵
- 本质矩阵是由对极约束定义的。由于对极约束是等式为零的约束,所以对 E 乘以任意非零常数后, 对极约束依然满足。我们把这件事情称为 E 在不同尺度下是等价的。
- 根据 E = t^R,可以证明 [3],本质矩阵 E 的奇异值必定是 [σ; σ; 0]T 的形式。这称为本质矩阵的内在性质。
- 另一方面,由于平移和旋转各有三个自由度,故 t^R 共有六个自由度。但由于尺度等价性,故 E 实际上有五个自由度。
E 具有五个自由度的事实,表明我们最少可以用五对点来求解 E。但是, E 的内在性质是一种非线性性质,在求解线性方程时会带来麻烦,因此,也可以只考虑它的尺度等价性,使用八对点来估计 E——这就是经典的八点法( Eight-point-algorithm);
考虑一对匹配点,它们的归一化坐标为: x1 = [u1; v1; 1]T , x2 = [u2; v2; 1]T。根据对极约束,有: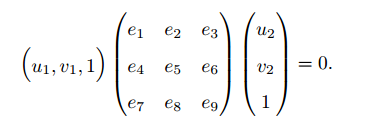
对极约束可以写成与 e 有关的线性形式:
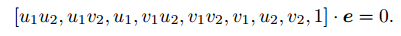
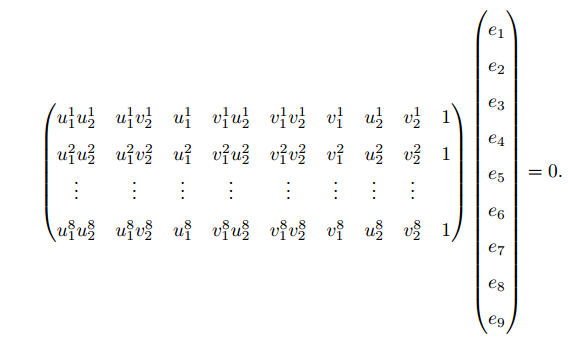
如果八对匹配点组成的矩阵满足秩为 8 的条件,那么 E 的各元素就可由上述方程解得。
奇异值分解
设 E 的 SVD 分解为: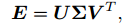
其中 U; V 为正交阵, Σ 为奇异值矩阵。根据 E 的内在性质,我们知道 Σ = diag(σ; σ; 0)。
在 SVD 分解中,对于任意一个 E,存在两个可能的 t; R 与它对应: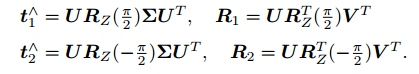
从 E 分解到 t; R 时,一共存在四个可能的解。

只有一种解, P 在两个相机中都具有正的深度。因此,只要把任意一点代入四种解中,检测该点在两个相机下的深度,就可以确定哪个解是正确的了。
注意:
根据线性方程解出的 E,可能不满足 E 的内在性质——它的奇异值不一定为 σ; σ; 0 的形式。这时,在做 SVD 时,我们会刻意地把 Σ 矩阵调整成上面的样子。
通常的做法是,对八点法求得的 E 进行 SVD 分解后,会得到奇异值矩阵Σ = diag(σ1; σ2; σ3),不妨设 σ1 ≥ σ2 ≥ σ3。取:
单应矩阵
单应矩阵( Homography) H 的东西,它描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上(比如墙,地面等),则可以通过单应性来进行运动估计。这种情况在无人机携带的俯视相机,或扫地机携带的顶视相机中比较常见。
单应矩阵通常描述处于共同平面上的一些点,设这个平面满足方程:
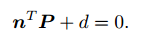
整理,得:

推导:
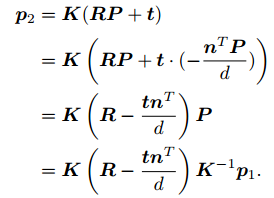
我们得到了一个直接描述图像坐标 p1 和 p2 之间的变换,把中间这部分记为H,于是
展开得:
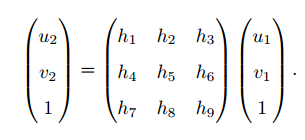
我们在实际处理中,通常乘以一个非零因子使得 h9 = 1(在它取非零值时)。然后根据第三行,去掉这个非零因子,于是有:
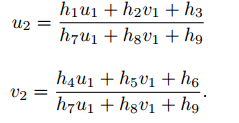
整理得:
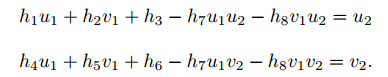
是自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出:

单应性在 SLAM 中具重要意义。当特征点共面,或者相机发生纯旋转的时候,基础矩阵的自由度下降,这就出现了所谓的退化( degenerate)。
现实中的数据总包含一些噪声这时候如果我们继续使用八点法求解基础矩阵,基础矩阵多余出来的自由度将会主要由噪声决定。
为了能够避免退化现象造成的影响,通常我们会同时估计基础矩阵 F 和单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵