KingdomAndCities 题解
题意
\(~~~~\) 给出 \(n,m,k\),求出具有 \(n\) 个点、\(m\) 条边、且前 \(k\) 个点的点度恰好为 \(2\) 的无向连通图个数,答案对 \(10^9+7\) 取模。
\(~~~~ 1\leq n,m \leq 50,0\leq k\leq \min(n,2)\)。
题解
\(~~~~\) 你看这个 \(k\) 是不是很小,所以不妨直接分类讨论 \(k\) 的取值。
\(\texttt{k=0}\)
\(~~~~\) 此时即求 \(n\) 个点 \(m\) 条边的无向连通图的个数。
\(~~~~\) 定义 \(f_{n,m}\) 表示 \(n\) 个点 \(m\) 条边的无向连通图个数,答案即 \(f_{n,m}\) 。
\(~~~~\) 正难逆不一定易,但我们可以尝试一下。总方案数显然是 \(\begin{pmatrix} \frac{n(n-1)}{2} \\ m \end{pmatrix}\) 。下面考虑不合法的方案数。
\(~~~~\) 按照连通性类似的套路,我们枚举 \(1\) 所在连通块的大小(下文记为 \(i,1\leq i\leq n-1\) ),并枚举分配给它多少条边(下文记为 \(j,i-1\leq j\leq \min(m,\frac{i(i-1)}{2})\) )。选择这样的点集的方案数是 \(\begin{pmatrix} n-1 \\ i-1 \end{pmatrix}\) ,此外连通块内部连边方案为 \(f_{i,j}\) ,外部随意连边,方案为 \(\begin{pmatrix} \frac{(n-i)(n-i-1)}2 \\ m-j \end {pmatrix}\) 。
\(~~~~\) 得到转移式:
\(~~~~\) 随便 \(n^4\) (当然远远不到)转移一下就行了。
查看代码
for(int N=1;N<=n;N++)
{
for(int M=N-1;M<=min(1ll*N*(N-1)/2,m);M++)
{
dp[N][M]=C(M,N*(N-1)/2);
for(int i=1;i<N;i++)
{
ll FAC=C(i-1,N-1);
for(int j=i-1;j<=min(M,i*(i-1)/2);j++) dp[N][M]=Add(dp[N][M],-Mul(FAC,Mul(dp[i][j],C(M-j,(N-i)*(N-i-1)/2))));
}
}
}
\(\texttt{k=1}\)
\(~~~~\) 我们来看一个点,它连向另外两个有连边的点有哪些可能(下面均展示一号点加入 \(2\) 号和 \(3\) 号点)。
\(~~~~\) 第一种,即加入在该边上,此时需要多一条边:
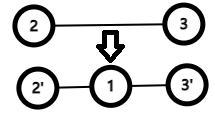
\(~~~~\) 第二种,加入成一个三元环,此时需要多两条边:
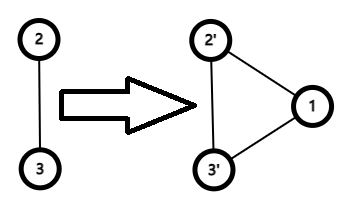
\(~~~~\) 需要注意的是,这样的加入都是不改变连通性的。
\(~~~~\) 现在,我们来考虑把特殊点取出来,其他点连成连通图的情况下,我们可以怎么做:
- 把这个点加入一条边,此时不含特殊点的图应该有 \(n-1\) 个点 \(m-1\) 条边,每条边都可以选,故答案为 \(f_{n-1,m-1}\times (m-1)\) 。
- 加入成一个三元环,此时不含特殊点的图应该有 \(n-1\) 个点 \(m-2\) 条边,每条边都可以选,故答案为 \(f_{n-1,m-2}\times (m-2)\) 。
\(~~~~\) \(k=1\) 时的答案就是上面的和。
查看代码
printf("%lld",Add(Mul(dp[n-1][m-1],m-1),Mul(dp[n-1][m-2],m-2)));
\(~~~~\) 这个部分另外还有一个 \(\mathcal{O(n^2)}\) 的做法,具体就是枚举这一个点连接的两个连通块的大小,最后加上只有一个连通块时随便连的方案数再减半(两边可能重复,比如 \(4\) 个点时把 \(1,2,3\) 合成一个块,另外 \(4\) 单列的块是算过的)即可。
查看代码
ll Ans=0;
for(int i=1;i<n;i++)
{
for(int E=i-1;E<m-1;E++)
{
int j=n-1-i,Ej=m-E-2;
Ans=Add(Ans,Mul(Mul(dp[i][E],dp[j][Ej]),Mul(C(i,n-1),Mul(i,j))));
}
}
return printf("%lld",Mul(Add(Ans,Mul(dp[n-1][m-2],Mul(n-1,n-2))),qpow(2,MOD-2)))&0;
\(\texttt{k=2}\)
\(~~~~\) 还是分类讨论:
\(~~~~\) 两个点连在一起,此时我们可以把它们看成一个点的捆绑,但需要注意这 “一个点” 是可以同时连某一个点的, 所以:
\(~~~~ ~~~~\) 它们连同一个点:原图方案 \(f_{n-2,m-3}\) ,任选原来的点,故答案为 \(f_{n-2,m-3}\times (n-2)\) 。
\(~~~~ ~~~~\) 它们连在一条边上:原图方案 \(f_{n-2,m-2}\) ,任选一条边,同时两个点可以交换位置,故答案为 \(2f_{n-2,m-2}\times (m-2)\) 。
\(~~~~ ~~~~\) 它们连成 “三元环”(本质上是四元环):原图方案 \(f_{n-2,m-3}\) ,任选一条边,同时两个点可以交换位置,故答案为 \(2f_{n-2,m-3}\times (m-3)\) 。
\(~~~~\) 两个点不连在一起,那分开讨论每一个连在边上还是连成三元环:
\(~~~~ ~~~~\) 它们都连成三元环,原图方案 \(f_{n-2,m-4}\) ,每个任选边,同时注意选到相同边不影响,故答案为 \(f_{n-2,m-4}\times (m-4)^2\) 。
\(~~~~ ~~~~\) 一个连在边上一个连成三元环,原图方案 \(f_{n-2,m-3}\) ,任选边时注意不能选到同一边(否则本质上就变成两个都加在边上,可以自行画图理解),两个点可以交换,故答案为\(2f_{n-2,m-3}\times (m-3)\times (m-4)\) 。
\(~~~~ ~~~~\) 两个都连在边上,此时讨论是否选同一边:
\(~~~~ ~~~~ ~~~~\) 选在同一边,那有一个点的边是不能靠原来在的边提供的的 ,答案 \(f_{n-2,m-3}\times (m-3)\) 。(或者你也可以认为这种方案的本质就是上面一种讨论情况选在同一条边,但注意如果按上面一种情况来想不能交换两个顺序,因为最后它的连边是一样的)
\(~~~~ ~~~~ ~~~~\)没选在同一边,原图方案 \(f_{n-2,m-2}\) ,任选两条不同的边,答案为 \(f_{n-2,m-2}\times (m-2)\times (m-3)\) 。
\(~~~~\) 答案就是上面的和。
查看代码
ll Ans=0;
// 3.1 两个点捆绑
// 3.1.1连同一个点
Ans=Add(Ans,Mul(dp[n-2][m-3],n-2));
// 3.1.2 加在一条边上
Ans=Add(Ans,Mul(Mul(dp[n-2][m-2],m-2),2));
// 3.1.3 加在三元环上
Ans=Add(Ans,Mul(Mul(dp[n-2][m-3],m-3),2));
// 3.2 两个点不捆绑
// 3.2.1 两个点都变成三元环
Ans=Add(Ans,Mul(dp[n-2][m-4],Mul(m-4,m-4)));
// 3.2.2 一个点三元环另一个加在边上
Ans=Add(Ans,Mul(2,Mul(dp[n-2][m-3],Mul(m-3,m-4))));
// 3.2.3 两个点都加在边上
// 3.2.3.1 加在同一条边
Ans=Add(Ans,Mul(dp[n-2][m-3],m-3));
// 3.2.3.2 加在不同的边
Ans=Add(Ans,Mul(dp[n-2][m-2],Mul(m-2,m-3)));
printf("%lld",Ans);