LCS(最长公共子序列问题)

LCS(Longest Common Subsequence)，即最长公共子序列。一个序列，如果是两个或多个已知序列的子序列，且是所有子序列中最长的，则为最长公共子序列。

原理：

事实上，最长公共子序列问题也有最优子结构性质。然后，用动态规划的方法找到状态转换方程。

记:Xi=﹤x1，⋯，xi﹥即X序列的前i个字符 (1≤i≤m)（前缀）

Yj=﹤y1，⋯，yj﹥即Y序列的前j个字符 (1≤j≤n)（前缀）

假定Z=﹤z1，⋯，zk﹥∈LCS(X , Y)。

若xm=yn（最后一个字符相同），则不难用反证法证明：该字符必是X与Y的任一最长公共子序列Z（设长度为k）的最后一个字符，即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时，问题化归成求Xm-1与Yn-1的LCS（LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1）。
若xm≠yn，则亦不难用反证法证明：要么Z∈LCS(Xm-1, Y)，要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立，若zk≠xm则有Z∈LCS(Xm-1 , Y)，类似的，若zk≠yn 则有Z∈LCS(X , Yn-1)。此时，问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为：max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。

由于上述当xm≠yn的情况中，求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度，这两个问题不是相互独立的：两者都需要求LCS(Xm-1，Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS，故问题具有最优子结构性质考虑用动态规划法。

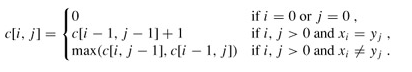
 public static int LCS(String x,String y){    
            int  [][] z=new int [x.length()+1][y.length()+1];    
            int i,j;    
            for( i=0;i<=x.length();i++)    
                z[i][0]=0;    
            for( j=0;j<=y.length();j++)    
                z[0][j]=0;    
                
            for(i=1;i<=x.length();i++){    
                for( j=1;j<=y.length();j++){    
                    if(x.charAt(i-1)==y.charAt(j-1)){    
                        z[i][j]= z[i-1][j-1]+1;    
                    }    
                    else    
                        z[i][j]=z[i-1][j] > z[i][j-1] ?z[i-1][j]:z[i][j-1];    
                }    
            }    
            return z[x.length()][y.length()];    
        }