斐波那契数列的实现（简单递归和动态规划）

一、简单递归的实现

 1 #include "stdafx.h"
 2 #include <string>
 3 using namespace std;
 4 int f(int n)
 5 {
 6     if (n == 0)
 7     {
 8         return 0;
 9     }
10     if (n == 1)
11     {
12         return 1;
13     }
14     return f(n - 1) + f(n - 2);
15 }
16 int _tmain(int argc, _TCHAR* argv[])
17 {
18     printf("%d", f(10));
19     getchar();
20     return 0;
21 }

　　求解斐波那契数列当中的n=5时的值这个问题的递归树如下图所示：

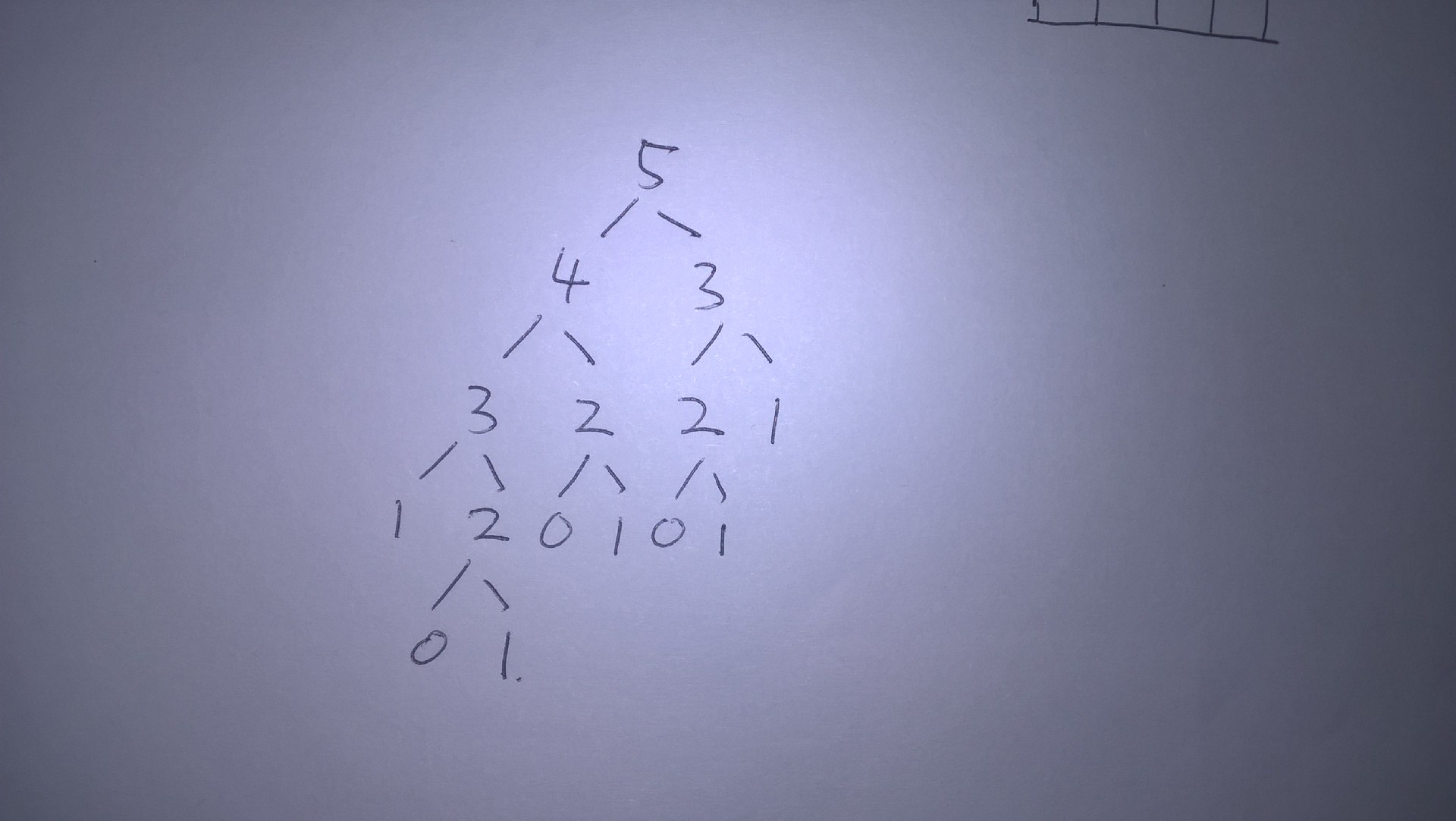
可见递归算法由于会多次计算同样的子问题而出现效率低下的问题，为了避免重复计算子问题，提升算法的效率，可以使用动态规划的思维来改进算法。

二、动态规划算法

1、具有备忘功能的自顶向下算法

使用一个数组来记录各个子问题的解，当再一次遇到这一问题的时候直接查找数组来获得解避免多次计算子问题。

 1 #include "stdafx.h"
 2 #include <string>
 3 using namespace std;
 4 int f(int a[],int n)
 5 {
 6     if (n == 0)
 7     {
 8         a[0] = 0;
 9         return 0;
10     }
11     if (n == 1)
12     {
13         a[1] = 1;
14         return 1;
15     }
16     if (a[n] >= 0)
17     {
18         return a[n];
19     }
20     a[n] = f(a, n - 1) + f(a, n - 2);
21     return f(a, n - 1) + f(a, n - 2);
22 }
23 int _tmain(int argc, _TCHAR* argv[])
24 {
25     int n = 10;//需要求解的数
26     int* a = (int*)malloc((n + 1)*sizeof(int));
27     for (int i = 0; i < n + 1; i++)
28     {
29         a[i] = -1;
30     }
31     printf("%d
子问题的解", f(a, n));
32     for (int i = 0; i < n + 1; i++)
33     {
34         printf("%d ", a[i]);
35     }
36     getchar();
37     return 0;
38 }

2、自底向上解决方案

　　先求解子问题再根据子问题的解来求解父问题，斐波那契数列的子问题图如下：

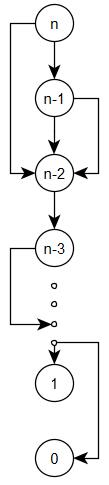
 1 #include "stdafx.h"
 2 #include <string>
 3 using namespace std;
 4 int f(int a[],int n)
 5 {
 6     a[0] = 0;
 7     a[1] = 1;
 8     for (int i = 2; i <= n; i++)
 9     {
10         a[i] = a[i - 1] + a[i - 2];
11     }
12     return a[n];
13 }
14 int _tmain(int argc, _TCHAR* argv[])
15 {
16     int n = 10;//需要求解的数
17     int* a = (int*)malloc((n + 1)*sizeof(int));
18     for (int i = 0; i < n + 1; i++)
19     {
20         a[i] = -1;
21     }
22     printf("%d
子问题的解", f(a, n));
23     for (int i = 0; i < n + 1; i++)
24     {
25         printf("%d ", a[i]);
26     }
27     getchar();
28     return 0;
29 }

　　自底向上的计算方法实现起来非常容易，分析算法，仅从形式上面分析算法可知，算法的时间主要消耗在计算数据规模为n的数组里面的数上面了，所以时间复杂度为O（n）。